Matematikkompasset
Matematikkompasset brukes til å utvide læreres praksis i møte med elever i matematikkvansker. Gjennom å visualisere samspill, intensjonene med opplæringen og matematiske handlinger kan dette redskapet bidra til å sette retning for elevers ønskede utvikling.
Det er laget flere oversikter over forskning på matematikkvansker. Analyser av temaene viser at forskningen i liten grad henger sammen med læringsarbeidet i skolen.
I henhold til A bibliography with some comments (Magne, 1996) som inneholder ca. 3000 titler, har forskning på matematikkvansker og dyskalkuli hatt et beskjedent omfang sammenlignet med forskning på læring og matematikklæring. I tillegg viser Magne at forskningen omfatter relativt få tema, med hovedfokus på regning med små naturlige tall i en kontekst av symbolog formalismekompetanse.
Denne kompetansen, som betyr å kunne håndtere matematiske symboler og formelspråk, utgjør et snevert fokus ettersom det bare er , som alle har gyldighet for matematikkundervisning på samtlige utdannelsestrinn (Undervisningsministeriet, 2002).
Fotnote: én av åtte matematiske kompetanser 1
1. Tankegangs-, problembehandlings-, modellerings-, resonnements-, representasjons-, symbol- og formalisme-, kommunikasjons- og hjelpemiddelkompetanse
I avhandlingen Om det inte är dyskalkuli – vad är det då? (Sjöberg, 2006) drøftes forskningslitteraturen på matematikkvansker i perioden 1993–2003. Kompleksiteten i feltet kommer frem gjennom inndeling i pedagogiske, psykologiske, sosiologiske og medisinsk-nevrologiske årsaksforklaringer (Ahlberg, 2001). Uansett hvilken forklaringsmodell som velges, konstaterer Sjöberg at en stor overvekt av forskningslitteratur på matematikkvansker hentes fra nevrologiske og nevropsykologiske felt.
I en nyere håndbok om dyskalkuli og matematikkvansker (Chinn, 2015) fastholdes det at matematikkvanskefeltet er i sin forskningsbegynnelse sammenlignet med forskning på lese- og skrivevansker, men at feltet stadig utvikles. I håndbokas 31 kapitler opprettholdes funnene fra Magne og Sjöberg. Matematikkvanskene beskrives fra flere perspektiv, men det store flertallet av artiklene handler om nevrologiske og psykologiske problemstillinger, og problemer knyttet til regning med små naturlige tall.
Denne artikkelen beskriver ikke et forskningsarbeid, men et forsøk på å anvende annen forskning for å utvide praksis rundt arbeidet med matematikkvansker. Hensikten er å utvide forklaringsmodellene og den tenkningen om matematikkvansker som til nå har vært særlig vektlagt. Det betyr et større fokus på omgivelsene og personen i samspill om aktiviteter som innbyr til varierte deltagelsesformer i matematikklæring.
Matematikkvansker med nye øyne
Et kompass er et navigasjonsredskap som angir retning. Når en matematikksituasjon er vanskelig, er det mange navigasjonsmuligheter. Flere parter skal sammen prøve å forstå situasjonen og kompleksiteten, som i et landskap. De skal utforme læringssituasjoner som gjør det mulig for grupper og enkeltelever å lære matematikk, delta i fellesskap og utvikle seg som personer, noe som krever samarbeid og samsending. Matematikkompasset (Daland & Dalvang, 2016) er et redskap som får frem viktige forhold som kan hjelpe til å sette fokus og retning for en ønsket utvikling. Kart og terreng er ikke gitt, men lokale svar kan skapes gjennom fornuftig kompassbruk.
Matematikkompasset er et redskap forfatterne har utviklet gjennom arbeidet med rådgivning og veiledning i det statlige spesialpedagogiske støttesystem, Statped. Oppdragene Statped får, handler ofte om å samarbeide med skoler og pedagogisk psykologisk tjeneste (PPT) om å undersøke og avhjelpe elever i matematikkvansker. Det kan dreie seg om enkeltelever i matematikkvansker, og hele skoler som opplever å ha for mange elever med lavt læringsutbytte i faget.
Grunntanken i Statped sine tjenester hviler på et inkluderende perspektiv. I dette arbeidet har vi som mål at vårt bidrag i samarbeidet om elever i matematikkvansker skal være preget av et sosiokulturelt perspektiv på mennesket og dets læring og utvikling. Et slikt syn bygger på at læring skjer gjennom bruk av språk og deltagelse i sosial praksis (Säljö, 2006).
Å få til samlesing av forskningsartikler knyttet til matematikkvansker er krevende. Lærerne har travle hverdager med hyppige handlingsvalg og mange vanskelige oppgaver, og som følge av en slik situasjon ønskes det ofte raske og pragmatiske løsninger, som helst skal kunne tas i bruk neste dag. I fagmøter med lærere og PPT er det likevel behov for et redskap for å angi retning på arbeidet og utvide det faglige fokus med særlig vekt på en matematikkfaglig og didaktisk ramme.
I arbeidet med ulike saker startet vår undring over hvilke faglige deler som var viktige å ha med, og som nå utgjør matematikkompasset. Delene er inspirert av læreplanen, som er et delt mandat for skoler, PPT og Statped.
Matematikkompasset kan tolkes som et medierende redskap mellom den aktuelle situasjonen og en ny situasjon som det er mulig å forestille seg, tilpasse og endre. Den russiske psykologen Lev Vygotskij utviklet ideen om mediering gjennom redskaper som utvidelser av stimulus og respons. Språk er ifølge Vygotskij et viktig redskap for å tenke. Mediering viser til at vi både fortolker og påvirker verden gjennom redskap (Säljö, 2006). Matematikkompasset visualiserer i tre sirkelskiver samspill mellom kontekst, opplæringens intensjoner og matematiske handlinger (se figur 1). Kompassmetaforen er valgt fordi redskapet er tenkt tatt i bruk når er usikre på veien som følges, og opplever at læringsutbyttet ikke er tilfredsstillende eller forsvarlig (Utdanningsdirektoratet, 2014).
Fotnote: skoler, foreldre eller elever 2
2. Om elevens rett til å bli hørt: FNs barnekonvensjon artikkel 12 og opplæringsloven § 5-4
Redskapet kan brukes for å analysere situasjoner, stoppe opp og orientere seg på nytt. Det er viktig å fokusere på noen få forhold om gangen og samtidig gi oppmerksomhet til helheten.
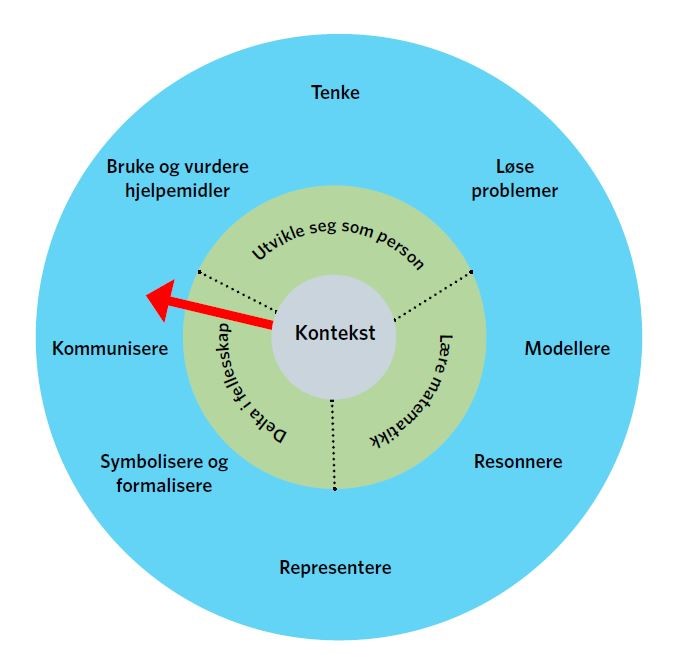
Matematikkompassets deler
Kontekst
Kontekstbegrepet brukes ofte i tilknytning til opplæring. Dyste (2001, s. 43) tar frem det latinske ordet «contextere» som betyr å veve sammen. Hensikten med å sette kontekst i midten på matematikkompasset er å få frem hvordan alle deler er integrerte, vevd sammen og at læring inngår i denne helheten.
I senere tid er kontekstbegrepet også anvendt i psykologisk utredningssammenheng. Jørn Nielsen argumenterer for nytenkning av utredningsbegrepet og dets anvendelse i praksis gjennom blant annet å legge vekt på de sammenhenger individet lever og vokser opp i.
Ethvert fenomen – og ethvert problem – eksisterer alltid i kontekst. Konteksten gir mening til fenomenet. […] Derfor kan den mindste analyseenhed aldrig være individet. (Nielsen, 2013, s. 41).
I et sosiokulturelt perspektiv på veiledning er det ønskelig å utvide fokus til å gjelde omgivelsenes svar på og samspill med eleven eller fenomenet, ikke alene å undersøke en elev eller et fenomen.
Opplæringens intensjoner
Delene i den mellomste sirkelen henger tett sammen med opplæringens intensjoner. En kan si at læreplanen setter opp tre vesentlige krav til skolen når det gjelder hva den skal få til for den enkelte elev (Werner og Håstein, 2014). Eleven skal lære fag i tråd med de mål som er fastsatt i læreplanen. Eleven skal utvikle seg som person. Og eleven skal delta i fellesskap med medelever. Intensjonene er rettet mot elevens fremtid og muligheter. Intensjonene er mer orientert mot prosesser enn produkter, og fremhever mestring fremfor vansker.
Litt forenklet sagt har det i utredningsarbeid vært en sterk tradisjon for å fokusere på elevens forutsetninger, forklart med vansker, gjennom å individuelt teste elevers evner, og å foreslå kompensatoriske individuelle tiltak i relasjon til testresultat. Delene i midterste sirkel kan sies å romme elevens forutsetninger, men er også ment å oppfordre til undersøkelse av nye muligheter som impliserer læring i et fellesskap. Hensikten er at støttesystemet sammen med skolen må begynne å lete etter nye forståelsesformer og samspillsmønster som kan gi eleven muligheter til å mestre.
Hensikten med matematikkompasset ser ut til å støttes opp av funn i Speed-prosjektet, som er et pågående forskningsprosjekt ved Høgskolen i Volda om spesialundervisning. Hovedsaken er å studere innholdet i og utbytte av spesialundervisning. Foreløpige resultater fra prosjektet peker på at vi behøver kunnskap og kompetanse på å utvide den ordinære opplæringen, fremfor å tilrettelegge for mer spesialundervisning utenfor fellesskapet (Tophol, 2015).
Matematiske handlinger
I den ytterste sirkel har vi plassert matematiske handlinger. Utvalget av handlinger (eller samhandlinger) er et spekter som elever kan bli invitert til å ta i bruk for å utvikle matematisk kompetanse, og for å arbeide mot intensjonene for opplæringen. Handlingene er ikke tilfeldige, men inspirert av Niss & Jensens beskrivelser av kompetanser og matematikklæring (Undervisningsministeriet, 2002). Kompetansebeskrivelsene var også viktige da læreplanen ble revidert i 2006 (LK-06).
I matematikkompasset er kompetansebeskrivelsene omgjort til handlinger, som hver især er utdypet med en forklarende tekst. Det skal være mulig å observere, gjenkjenne, beskrive og utvikle handlingene i matematikkopplæringen; tenke, løse problemer, modellere, resonnere, representere, symbolisere og formalisere, kommunisere, bruke teknologi og hjelpemidler (Daland og Dalvang, 2016).
Matematikkompassets helhet og dynamikk
Matematikkompasset utgjør tre sirkelskiver utenpå hverandre. Den midterste sirkelen kan roteres. En pil er festet i midten og rekker ut til ytterste sirkel, pilen kan også roteres. Rotasjonene av både midterste sirkel og pilen i ytterste sirkel gjør det mulig å velge hvilke intensjoner og handlinger i matematikkopplæringen som fokuseres.
En kan tenke seg en bevegelse fra en kontekst, som kan være en vanskelig opplæringssituasjon, til intensjoner og videre til handlinger, altså fra midten og utover. Eller en kan velge motsatt retning, og starte med en handling. Begge retninger eksemplifiseres i figurene 2, 3 og 4.
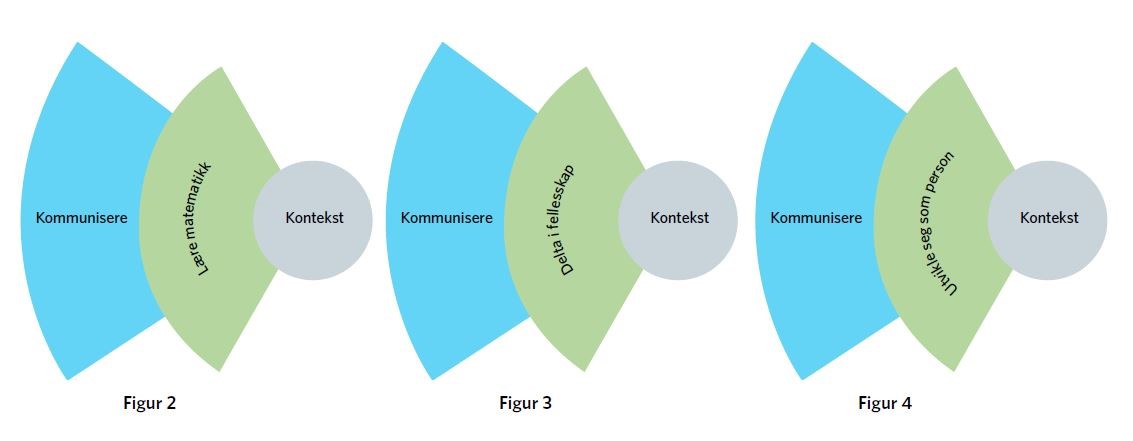
Her velges handlingen å kommunisere i relasjon til henholdsvis lære matematikk, delta i fellesskap og utvikle seg som person. Lærere, foreldre og rådgivere kan undersøke ved å spørre seg: Hva slags formuleringer og fremføringer uttrykkes i læringssituasjonen? Hvordan kommuniseres det og av hvem? Hvilke muligheter er det til å ta i bruk og utvikle sin kommunikasjon i, om og med matematikk?
I Matematikkompasset er det utviklet en handlings- og mulighetsmatrise der tilsvarende spørsmål foreslås til alle handlingene i relasjon til hver og en av intensjonene.
Hver enkeltdel i Matematikkompasset kan assosieres til en rekke artikler og ideer innenfor blant annet spesialpedagogikk og matematikkdidaktikk. Vi arbeider videre med å beskrive opplæringssituasjoner der Matematikkompasset er tatt i bruk, og har fått lokalt innhold.
Hensikter
Matematikkompasset har vært et utviklingsarbeid i praksis, influert av forskning på læring i et sosiokulturelt perspektiv. Det er ment å være et medierende redskap for elever, lærere og rådgivere i PPT og Statped i arbeidet med å forstå og utvikle opplæringssituasjoner. Det innebærer å undersøke sammenhenger mellom hvordan unge mennesker utvikler seg og er nysgjerrige på det å lære matematikk, delta sammen med andre, og hvordan det matematiske læringsmiljøet innbyr til, setter rammer for og støtter opp om slik aktivitet.
For tiden pågår et utviklingsarbeid der PP-rådgivere prøver ut betydningen av å bruke Matematikkompasset i egen praksis i møte med skoler og elever i matematikkvansker. Utviklingsarbeidet handler om å utvide den ordinære opplæringen for elever i matematikkvansker. (Daland, Dalvang, Aaraas, Lund og Slettebø, 2015)
Redskapet har utvidet vår forståelse av læreplanen. Vi har fått et felles språk for å utforske aktivitetene vi kan observere i klasserommene, og for å snakke med lærerne om å utvide elevenes muligheter for deltagelse. Matematikkompasset utvikler vårt eget sakkyndighetsarbeid.
Vi er blitt bevisste på at spørsmålene vi stiller til skolene, og at undersøkelsene vi utfører også må gjøres i klasserommet. Dette har gjort at vi har fått et annet blikk på de pedagogiske rapportene fra skolene og hvordan vi må utvikle disse til å favne konteksten elevene er i. Gjennom å bruke matematikkompasset i samarbeid med lærerne kan vi utvide elevenes muligheter til å lære matematikk. (Aaraas, Lund og Slettebø, rådgivere i Midt-Telemark PPT)
Matematikkompasset er ikke en fullstendig didaktisk modell. De ulike delene er tenkt å bidra til en bredere forståelse av en vanskelig matematikksituasjon, hva matematikk kan handle om, hva som allerede vektlegges og hva som kan utvikles videre.
Foreløpige bruksområder
- For å planlegge, gjennomføre og vurdere rikere og mer variert opplæring i faget.
- For å undersøke samhandlinger i matematiske opplæringssituasjoner.
- For å støtte opp under utredning, tilråding og IOP-dokumenter.
- For å bidra med helhet og fokus i tverrfaglige møter.
Betenkninger
Forfatterne har gjort en rekke forsøk på ordvalg i ytterste sirkel, for å beskrive det matematiske mulighetsspekteret, og vi har gang på gang gått tilbake til nåværende handlinger, da de er sterkt knyttet til læreplanen. Vi er bevisst på at kompetansebeskrivelsene i kom-prosjektet (Niss og Jensen, 2002) ikke lever isolert, men må ses i sammenheng, og det samme mener vi gjelder handlingene. Tenke er for eksempel ofte sterkt knyttet til handlingene løse problemer, kommunisere og resonnere.
Kompleksiteten i kompetansebeskrivelsene (Undervisningsministeriet, 2002) kan ha blitt forringet av å være omgjort til verb/handlinger. Handlingene kan i tillegg lett tolkes spontant i et hverdagsspråk, som for eksempel tenke. I Matematikkompasset er hver handling forsøkt utdypet, og det i seg selv har vært et utfordrende arbeid som vi presenterer med ydmykhet. Tenke er forsøkt forklart som «stille matematiske spørsmål og ha blikk for hvilke typer svar som forventes. Bruke matematiske begreper, skille mellom ulike matematiske forklaringer og generalisere.»
En kan si at Matematikkompasset utgjør en forenkling, sett i lys av matematikkdidaktisk forskning. Men i en pragmatisk matematikkvanskekontekst, med ofte innsnevrede læringsmuligheter som tilbys for elever i matematikkvansker, er det et forsøk på å utvide det handlingsrommet elever i matematikkvansker får, og sette fokus og retning for en ønsket utvikling.
Litteraturhenvisninger
Ahlberg, A. (2001). Lärande och delaktighet. Lund: Studentlitteratur. Chinn, S. (2015). (Ed.) The Routledge International Handbook of Dyscalculia and Mathematical Learning Difficulties. London and New York: Routledge.
Daland, E. & Dalvang, T. (2016) Matematikkompasset. Statped. Læringsressurs. <http://www.statped.no/fagomrader-og-laringsressurser/finn-laringsressurs/sammensatte-larevansker/matematikkompasset/>
Daland, E., Dalvang, T., Aaraas, R.M., Lund, B.H., & Slettebø R.B. (2015). Å videreutvikle utrednings- og veiledningskompetanse for matematikkmestring. Presentasjon på konferansen Fra vanske til mestring. Kristiansand, 21.okt. 2015.
Dysthe, O. (2001). Dialog, samspell og læring. Oslo: Abstrakt forlag.
Kunnskapsdepartementet (2006) Læreplanverket for Kunnskapsløftet. Oslo: Utdanningsdirektoratet.
Magne, O. (1996). Bibliography of Literature on Dysmathematics. Malmö: Department of Educational and Psychological Research.
Nielsen, J. (2013). Utredning i kontekst. Utredninger – i vor tid. Pædagogisk Psykologisk Tidsskrift. Psykologi i kommunen, (1), 39-48.
Säljö, R. (2006). Læring og kulturelle redskaper. Oslo: Cappelen Akademisk. Sjöberg, G. (2006). Om det inte är dyskalkulivad är det då? Umeå: Umeå Universitet.
Tophol, A.K. (2015). SPEED-prosjektet – Kva kan vi lære av det? Presentasjon på konferansen Fra vanske til mestring. Kristiansand, 22.okt. 2015.
Undervisningsministeriet (2002). Kompetencer og matematiklæring. (Red.) M. Niss, og T.H. Jensen. København: Undervisningsministeriets forlag. <http://pub.uvm.dk/2002/kom/>
Utdanningsdirektoratet (2014). <http://www.udir.no/Regelverk/tidlig-innsats/Veilederene-i-fulltekst/Spesialundervisning/> websøk: 10.11.15.
Werner, S. & Håstein, H. (2014) tilpasset opplæring i fellesskapets skole. I: Mette Bunting (Red.), Tilpasset opplæring – i forskning og praksis. Oslo: Cappelen Damm Akademisk.