Pensjonssparing til matematikkeksamen– i 1952 og i 2017
Pensjonssparing er tema i to matematikkoppgaver gitt til eksamen med 65 års mellomrom.
Oppgavene har fellestrekk som gjør det mulig å drøfte likheter og forskjeller i kompetansen som kreves for å løse dem. Var matematikkoppgaven fra «gamle dager» lettere eller vanskeligere enn oppgaven gitt i våre dager?
Våren 2017 ble det gitt en oppgave til eksamen i Matematikk S2 som var svært lik en oppgave gitt til Examen artium på reallinjen i 1952. Da jeg leste eksamensoppgaven fra 2017 virket den kjent. Jeg så at den hadde mange fellestrekk med en oppgave jeg hadde sett i min mors minnebok fra russetiden hennes i 1952. Begge oppgavene handler om å skaffe seg en livrente – eller om pensjonssparing, som vi sier i dag. Videre handler begge om utbetalingene av det oppsparte beløpet.

Språk og layout
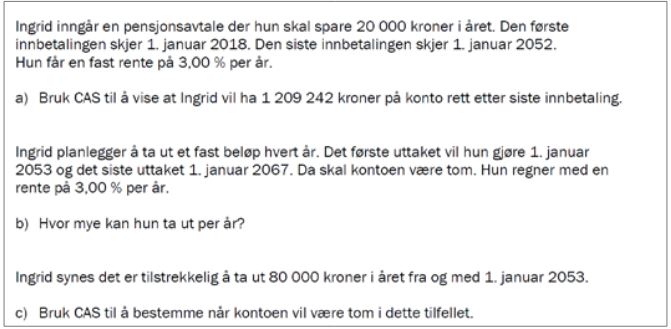
En mann i 1952 (se figur 1) og Ingrid i 2017 (se figur 2) setter av en fast sum hvert år og får en årlig rente på 3 %. Selv om oppgaven fra 1952 ikke er delt i a, b og c-oppgave, er den like fullt tredelt. I figur 1 ser vi at moren min har gjort noen markeringer i teksten for å lette oppdeling og fokusere på sentrale punkter. Dette får kandidatene i 2017 presentert gjennom tre tydelig adskilte deloppgaver.
I læreplanen for Matematikk S2 heter det: «Å kunne lese i matematikk for samfunnsfag innebærer å trekke matematisk relevant informasjon ut av en tekst» (Kunnskapsdepartementet, 2006). Hvor vanskelig det vil være å lese og tolke teksten, er avhengig av flere språklige trekk (Andresen, Fossum, Smestad & Rogstad, 2017, kap. 7). En ser at eksamensoppgaven fra 1952 er mer tekstrik, har flere lange og sammensatte ord, lengre setninger og mer komplekse ytringer sammenlignet med eksamensoppgaven fra 2017. Den vil derfor være vanskeligere å lese og forstå enn oppgaven fra 2017.
Første deloppgave – sparing til pensjon
For å løse oppgavenes første del vil eksamenskandidatene begge årene måtte kjenne igjen oppgavetypen og vite at løsningen finnes som summen av en geometrisk rekke. De må ut fra oppgaveteksten kunne finne de størrelsene de trenger å fylle inn i formelen.
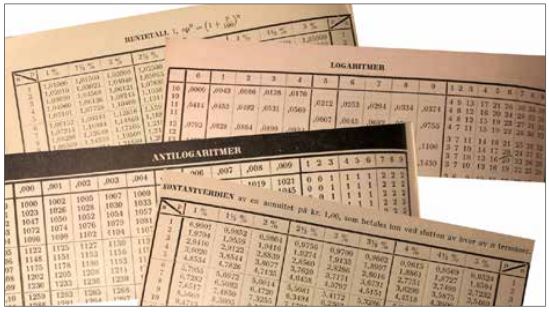
I 1952 måtte eleven huske summasjonsformel for geometrisk rekke, kunne slå opp i tabell over rentetall og enten bruke algoritmer for multiplikasjon og divisjon eller logaritmereglene og logaritmetabell i utregningen (se figur 3).
Kontrasten blir stor når vi hopper 65 år fram i tid. I 2017 kunne eleven bruke alle hjelpemidler (bortsett fra kommunikasjon) og har mulighet til å slå opp formler og fremgangsmåter i lærebøker eller i egne notater. Det er krav om å bruke i løsning av oppgaven, men ingen krav til hvordan verktøyet brukes.
Hvor vanskelig er oppgaven?
I tillegg til språket i oppgavene og de tilgjengelige hjelpemidlene, må opplæringen som er gitt tas i betraktning når vanskegraden skal sammenlignes. Det kan derfor være nyttig å gå til de aktuelle læ-rebøkene i henholdsvis 1952 og 2017 og undersøke om matematisk innhold og oppgavetype bør være kjent for elevene.
En lærebok eleven kunne hatt i 1952 er Matematikk for gymnasets reallinje, . Kapittelet «Geometriske rekker i renteregningen» i denne boken gir detaljerte eksempler tilsvarende første del av oppgaven. Generelt byr denne læreboken på færre oppgaver enn vi ser i dagens matematikkbøker, men nok til å konkludere med at oppgavetypen og algoritmene som trengs i løsningen bør være kjent. Siden boken ikke var tilgjengelig for eleven under eksamen, kunne ikke eksemplene brukes direkte som guide i løsningen. Den muligheten hadde derimot de som tok eksamen i 2017, selv om det var noe forskjell på de tre . Sinus matematikk S2 har et eksempel med formulering tilsvarende eksamensoppgaven og har også med løsning der CAS i GeoGebra brukes (Oldervoll, Orskaug, Vaaje, Svorstøl & Hals, 2015, s. 37-38) og det samme finner vi i Matematikk S2 (Heir, Borgan, Engeseth, Haug & Moe, 2016, s.101-102).
I Sigma matematikk S2 er det et lignende eksempel (Sandvold et al., 2015, s. 82), men innskuddet skjer i begynnelsen av året og beregnet oppsparing i slutten av året. I en oppgave i samme oppslag, er betingelsene de samme som i eksamensoppgaven og en slik oppgave med løsning finner vi også i kapitteltesten (ibid. s. 93, s. 220). I Sigma matematikk S2 er det ikke brukt CAS i løsningene og det er derfor ingen hjelp å hente i læreboken når det gjelder dette kravet. Siden alle hjelpemidler er tillatt når denne oppgaven løses i 2017, vil elevene som hadde Sinus matematikk S2 og Matematikk S2 kunne bruke eksemplene i boken direkte som guide i løsningen. Elevene som hadde Sigma matematikk S2 trenger i tillegg bruksanvisninger for CAS.
Selv om det er likheter mellom a-oppgaven i 2017 og oppgaven i første avsnitt i 1952, er det også vesentlige forskjeller. Eleven måtte i 1952 være trygg på at antall år de hadde regnet ut på bakgrunn av teksten, var riktig og at formelen var husket riktig. Evne til å vurdere om svaret er rimelig vil også være en fordel siden det skal brukes videre i oppgaven. Ikke noe av dette var nødvendig for elevene i 2017. Svaret var oppgitt som en del av oppgaveteksten, så selv om eleven i utgangspunktet hadde feil i en eller flere av størrelsene som må utledes fra teksten, vil det ta kort tid å prøve seg fram med andre tall for å få fasitsvaret. Mens man i 1952 risikerte følgefeil i de neste spørsmålene, kunne man i 2017 bruke det oppgitte svaret i oppgave a når oppgave b og c skulle løses.
Andre deloppgave – uttak av pengene
Videre handler begge oppgavene om uttak av det oppsparte beløpet i faste årlige beløp. I læreboken fra 1942 finner vi delkapittelet «Forbruk av kapital ved annuiteter. Tilbakebetaling av lån ved annuiteter.» (Alexander, 1942, s. 194ff ). Det kapittelet ville elevene som tok eksamen i 2017 også hatt glede av. Annuitetslån behandles grundig i de tre lærebøkene som var aktuelle i 2017, mens forbruk av kapital ved annuiteter, som er tema i de to eksamensoppgavene, i liten grad berøres.
Det kan tyde på at eksamensnemnda og lærebokforfatterne har ulik tolkning av kompetansemålet «Mål for opplæringen er at eleven skal kunne løse praktiske problemer i forbindelse med sparing , lån og avbetalingskjøp ved å bruke rekker.» (Kunnskapsdepartementet, 2006). Gjennomgangen av lærebøkene som ble brukt i 2017, viser at lærebokforfatterne ikke har vektlagt forbruk av kapital ved annuiteter, mens eksamensnemnda både og altså våren 2017, har med oppgaver som tester kompetanse på dette området.
Tidligere leder av eksamensnemnda for programfagene i matematikk i videregående skole, Inge Grythe, ser på eksamen som et sentralt virkemiddel for å endre en praksis (Grythe, 2009). Hans artikkel fokuserer spesielt på den todelte eksamen som har en del uten hjelpemidler og en del med hjelpemidler. Denne endringen var varslet på forhånd, men når det skjer en presisering av læreplanen gjennom eksamensoppgaver innenfor tema som ikke er behandlet i lærebøkene, blir det en ubehagelig overraskelse for elever og lærere.
Siden lignende eksamensoppgave var gitt i 2015, kan det ha endret praksis slik at forbruk av kapital ved annuiteter har fått mer plass i undervisningen enn det vi finner i lærebøkene. Ingen av bøkene har eksempler tilsvarende b-oppgaven i 2017 og de to som har lignende oppgaver, har dem plassert i kapitteltesten. Selv om elevene kan ha brukt tidligere eksamensoppgaver i forberedelsene til eksamen, vil erfaringen med oppgavetypen være liten og elevene må overføre kunnskap de har fra regning på annuitetslån til situasjonen med årlige utbetalinger. Oppgaven vil derfor kreve evne til problemløsning slik det beskrives i Eksamensveiledningen i matematikk (Utdanningsdirektoratet, 2017b, s. 19). Dersom eleven kommer fram til riktig uttrykk for den geometriske rekken, vil likningsløsning ved bruk av CAS være vesentlig enklere enn løsning uten dette hjelpemiddelet.
I 2017 regner elevene videre med en rente på 3 % og uttakene starter året etter at innbetalingene slutter. Summen av nåverdiene av utbetalingene skal være innestående på konto (beløpet vi har fra oppgave a). I 1952 var det lagt inn noen ytterligere utfordringer i denne delen av oppgaven. Renten holdes først på 3 % i noen år mens pengene står urørt. Når utbetalingene starter, går den årlige renten ned til 2,5 %. Der elevene i 2017 kunne bruke CAS og i praksis slippe å løse likningen selv, måtte elevene i 1952 både løse likning og regne manuelt. De elevene som i 1952 hadde hjelpemiddelkompe-tanse utover den som er presentert i læreboken, kan bruke tabellene over kontantverdier (Olden & Østraat, 1952, s. 25) og få en noe enklere ut-regning. I 1952-læreboken er det eksempler og oppgaver som til en viss grad er like eksamens-oppgaven (Alexander, 1942), men det er ingen med utsettelse av utbetaling og endring i rente. Eksamensoppgaven vil derfor kreve noe evne til problemløsning.
Problemløsning til slutt i 1952
Hvis elevene som tok eksamen i 2017 kom seg gjennom b-oppgaven der det årlige beløpet var ukjent, bør c-oppgaven der beløpet er kjent, og antall utbetalinger ukjent, ikke gi store utfordringer. I denne delen er ulikheten mellom oppgaven fra 1952 og 2017 størst. I 1952 møtte eleven helt nye utfordringer. I motsetning til i de to første delopp-gavene og i Matematikk for gymnasets reallinje, bind II (Alexander, 1942) finnes det verken eksempler eller oppgaver som ligner denne oppgaven. I 1952 måtte elevene derfor ha høy problemløs-ningskompetanse for å lykkes med denne delen.
Hjelpemidlenes betydning
Elevene som var oppe til eksamen i 1952 kunne bruke tabeller og regnestav, mens elevene i 2017 skal bruke CAS. Det er presisert i forhåndssensurrapporten at det kun skal gi halv uttelling hvis CAS ikke er brukt i løsninger der dette kreves (Utdanningsdirektoratet, 2017c). Uansett hvilke hjelpemidler som brukes, vil det ta tid å bli for-trolig med bruken av dem. Det som er åpenbart er at det tar vesentlig lengre tid å gjennomføre løsningen når tabellene er viktigste hjelpemiddel slik det var i 1952. Da ble også ferdigheter i bruk av de fire regneartene, likningsløsning og bruk av logaritmereglene testet, i tillegg til bruk av geometriske rekker. Disse ferdighetene testes i våre dager på den delen av eksamen som er uten hjelpemidler.
Danske forskere har funnet eksempler på at bruk av CAS innenfor noen tema kan føre til at den dypere matematiske forståelsen uteblir og i sin tur leder til manglende forståelse og evne til å evaluere løsninger og svar ( Jankvist & Misfeldt, 2015). I dette tilfellet er det ingen grunn til å tro at CAS gir opphav til misforståelser knyttet til oppgavetypen. Gjennomgangen av deloppgavene viser at det er nødvendig med en forståelse for regning med annuiteter som ikke påvirkes av verktøyene som er til rådighet. CAS gir mulighet til på kort tid å prøve og feile, men det er vanskelig å se at verktøyet i seg selv kan gi opphav til misforståelser. Det er heller ikke grunn til å tro at tabeller fremfor digitale hjelpemidler skal skape noen større matematisk forståelse i denne oppgavetypen.
For elever som skal opp til eksamen, er det en fordel med en viss forutsigbarhet (Elwood, Hopfenbeck & Baird, 2017). Ved eksamen i 2017 var det i noen grad tilfelle siden elevene har tilgang til tidligere eksamensoppgaver og eksamensveiledning. I den siste finnes detaljert oversikt over hvilke formler de skal kunne uten hjelpemidler (Utdanningsdirektoratet, 2017b, s. 40) og et eksempel på besvarelse med bruk av CAS i en oppgave fra R2 (ibid. s. 14-15), men det finnes ingen oversikt over hva elevene skal beherske ved hjelp av CAS.
Eksamen i pensjonssparing mer komplisert før
Gjennomgangen av de enkelte deloppgavene viser at både språklig og matematisk må oppgaven gitt i 1952 sies å være mer krevende enn oppgaven gitt i 2017. Med et enklere språk, blir det lettere å trekke ut den nødvendige informasjonen til oppgaveløsningen. Samtidig heter det i formålet for dette matematikkfaget:
Arbeid med programfaget gir øvelse i modellering. Det skal gi elevene anledning til å uttrykke praktiske problemer og fenomener fra virkeligheten i et matematisk formelspråk og deretter behandle dem ved hjelp av matematiske metoder. Disse ferdighetene skal gi elevene en nøkkel til å forstå og analysere viktige samfunnsproblemer. (Kunnskapsdepartementet, 2006)
De matematiske utfordringene i virkeligheten kommer sjelden i tydelig avgrensede deloppgaver, og hvis svaret er oppgitt slik det var i a-oppgaven i 2017, regnes oppgaven som løst og unødvendig å regne på. Hjelpemidlene gjør at når den ma-tematiske modellen er funnet, kan løsningene gjennomføres mye raskere i våre dager. Det kan gi større rom for utfordringer og krav til problemløsning enn tidligere. I dette eksempelet har ikke det vært tilfelle og utfordringene var mindre i 2017 enn i 1952.
Litteraturhenvisninger
Alexander, A. (1942). Matematikk for gymnasets reallinje II. Oslo: H. As-chehoug & Co. (W. Nygaard).
Andresen, S., Fossum, A., Rogstad, J. & Smestad, B. (2017). På prøve. Evaluering av matematikkeksamen på 10. trinn våren 2017. (Fafo-rapport 36/2017). Oslo: Fafo.
Elwood, J., Hopfenbeck, T., Baird, J.-A., (2017). Predictability in high-stakes examinations: students’ perspectives on perennial assessment dilemma. Research Papers in Education, 32(1), 1-17
Grythe, I. (2009). Mot et kunnskapsløft. Tangenten – Tidsskrift for matema-tikkundervisning, 1/2009, 43-51.
Heir, O., Borgan, B., Engeseth, J., Haug, T. & Moe, H. (2016). Matematikk S2. (2. utg.). Oslo: H. Aschehoug & Co. (W. Nygaard).
Jankvist, U. & Misfeldt, M. (2015). CAS-induced difficulties in learning mathematics? For the Learning of Mathematics, 35(1), 15-20.
Kunnskapsdepartementet (2006). Læreplan i matematikk for samfunnsfag – programfag i utdanningsprogram for studiespesialisering (MAT4-01). Hentet fra: https://www.udir.no/kl06/MAT4-01
Olden & Østraat (1952). Matematiske og fysiske tabeller for gymnaset. (13. utg.). Oslo: H. Aschehoug & Co. (W. Nygaard).
Oldervoll, T., Orskaug, O., Vaaje, A., Svorstøl, O. & Hals, S. (2015). Sinus matematikk S2. Oslo: Cappelen Damm AS.
Sandvold, K.E., Øgrim, S., Bakken, T., Pettersen, B., Skrindo, K., Hylland, K.T., Thorstensen, R. (2015). Sigma matematikk S2. (2. utg.).Oslo: Gyldendal Norsk Forlag AS.
Utdanningsdirektoratet (2017a). Eksamen. REA3028 Matematikk S2. Hentet fra: <https://sokeresultat.udir.no/eksamensoppgaver.html>
Utdanningsdirektoratet (2017b). Eksamensveiledning – om vurdering av eksamensbesvarelser 2017. Matematikk. Sentralt gitt skriftlig eksamen. Studieforberedende og yrkesfaglige studieprogram. Kunnskapsløftet LK06. Hentet fra: <https://sokeresultat.udir.no/eksamensoppgaver.html>
Utdanningsdirektoratet (2017c). Forhåndssensurrapport. REA3028 Matematikk S2. https://sokeresultat.udir.no/eksamensoppgaver.html