Fonologisk bevissthet og matematikkvansker

Det foreligger en rekke nordiske og internasjonale publikasjoner fra Hå-prosjektet. Noen av disse er å finne som artikler i Spesialpedagogikk (Askeland, 2005; Ostad, 2003, 2007, 2008). I den foreliggende artikkelen er fortsatt privat taleinternalisering en sentral variabel. Men her dreier det seg om (1) hvorvidt fonologisk bevissthet er positivt relatert til privat taleinternalisering, og (2) hvorvidt svaret på dette spørsmålet varierer som funksjon av elevenes alder og ferdighetsnivå i matematikk.

Det var først etter at vi hadde gjennomført en intervensjonsundersøkelse der fokus rettet seg mot det å stimulere utviklingen av privat tale (Askeland, 2005; Ostad, 2008), at det for alvor ble aktuelt å ta frem for forskningsmessig bearbeidelse tidligere innsamlede data om fonologisk bevissthet blant elever med og uten matematikkvansker. Siden den foreliggende artikkelen direkte bygger videre på data om utviklingen av privat tale, data som tidligere er publisert i Spesialpedagogikk (Ostad, 2007), blir det her kun referert til hovedtendensene i resultatene derfra.

Privat tale

I artikkelen inkluderer privat tale all tale som er akommunikativ, det vil si tale som ikke direkte adresseres til en eller flere tilhørere. «Med denne avgrensningen fungerer privat tale som en paraplybetegnelse som dekker så vel ytre privat tale som indre, såkalt subvokal tale» (Ostad, 2010, s. 199).

I sin beskrivelse av barns taleutvikling hevder Vygotsky (1934/1986) at barns ekspressive språk gradvis blir internalisert til en stille indre tale, og at indre tale bidrar til økt selvregulering, det vi si at den er et redskap for regulering (kontroll) av tanker og atferd. En rekke forskere har bidratt til å synliggjøre det karakteristiske utviklingsforløpet av privat tale. Her blir det kalt privat taleinternalisering. Det viser seg at i førskolealder og tidlig skolealder blir privat tale byttet ut med en stille indre tale (Berk, 1992; Winsler & Nagleri, 2003).

I tillegg til å rette søkelyset mot internaliseringen av privat tale har forskere tatt for seg en rekke andre aspekter ved fenomenet. Av særlig stor relevans for innholdet i denne artikkelen er forskning på privat tales relasjon til faglige prestasjoner (Berk, 1992; Winsler & Nagleri, 2003), bruken av privat tale blant elever med matematikkvansker (Ostad & Sorensen, 2007) og privat tale som fremhentingsredskap av informasjon fra kunnskapslageret (Ostad, 2008, 2010).

Fonologisk mangelfullhet

Det kognitive grunnlaget for lesning har vært gjenstand for en lang rekke undersøkelser. I de senere årene har særlig fonologisk prosessering (språklydprosesser) stått i fokus, og variasjonene i barns leseferdighet (decoding) er kjent for å korrelere høyt med mål for fonologiske ferdigheter (Durand, Hulme, Larkin, & Snowling, 2005; Wagner & Torgesen, 1987). Det er med basis i longitudinelle korrelasjonsstudier at forskere i stor grad er samstemte i at visse evner til fonologisk prosessering, det vil si kapabilitet til å bruke fonologisk eller lydbasert informasjon i skriftlig eller muntlig språkbruk, influerer kausalt på utviklingen av leseferdighet. En av de mest samlende hypotesene rettet mot hovedårsakene til dysleksi er at de personene det her dreier seg om, har spesifikk svekkelse med hensyn til representasjon, lagring og/eller fremhenting av (retrieval) språklyder (Ramus & Szenkovits, 2008; Snowling, 2001).

Det er et veletablert faktum at individuelle forskjeller når det gjelder ferdigheter i lesning og matematikk, kan være substansielt forankret, basert på at de to fagene har en del felles komponenter (Ackerman & Dykman, 1995; Ostad, 1999). Men også læreprosessen i de to fagene synes å ha felles komponenter. Det vises særlig ofte til at verbale koder blir aktivisert som ledd i oppgaveløsningen også i matematikk (Campbell, 1998; Swanson, Ashbaker & Lee, 1996). Det er derfor logisk å slutte at evne til fonologisk prosessering også vil influere på elevenes matematikklæring (Geary, 1993; Hecht et al., 2001). En nærliggende hypotese har derfor vært at elevenes ferdighet i skriftspråk og matematikk vil korrelere i samme grad som ferdighet i de to fagene er influert av de samme fonologiske evnene (Geary, 1993; Hecht et al., 2001).

Det synes i dag å være generelt akseptert at fonologisk prosessering representerer en kritisk faktor også når det gjelder tilegnelse av matematikkunnskaper (Berk, 1992; Hecht et al., 2001). Derfor har fonologiske lagringshypoteser kommet i fokus. Innenfor rammen av slike hypoteser blir det hevdet at aritmetiske basisenheter, det vil si enkle kombinasjoner i de fire regningsartene (4 + 3 = 7, 4 x 6 = 24 osv.), kan lagres i et lydbasert format (Cohen & Dehaene, 2000). Dette formatet kan være hensiktsmessig for effektivt å hente frem basisenhetene fra langtidsminnet under oppgaveløsningen (Geary et al., 2000). Når elever med matematikkvansker i liten grad, eller praktisk talt ikke, benytter retrieval-strategier under oppgaveløsningen (Ostad 1997, 1998), kan det skyldes at elevene enten ikke har lagret aritmetiske basisenheter på lydbasert basis, eller at elevene ikke har fått utviklet lydbaserte redskaper (prosesser) for å hente frem basisenheter under oppgaveløsningen (Geary, 1993; Ostad, 2010).

I en undersøkelse (Ostad & Sorensen, 2007) som ble gjennomført i et longitudinelt perspektiv, viste resultatet at det blant elever uten matematikkvansker foregikk en utvikling fra mindre til mer internalisert privat tale og fra mindre til mer internalisert strategibruk. Blant elever med matematikkvansker syntes internaliseringen både av privat tale og strategibruk å stanse opp på et tidlig utviklingsnivå. Disse resultatene dannet grunnlaget for hypotesen om at aritmetiske basisenheter blir lydbasert lagret og hentet frem fra kunnskapslageret som funksjon av det nivået barnet har nådd i internaliseringen av privat tale (fra hørbar tale til privat tale i stillhet). Derfor bidro undersøkelsen til å sannsynliggjøre at de karakteristiske retrievalvanskene som gjør seg gjeldende blant elever med matematikkvansker, kan gjenspeile deres manglende eller mangelfulle fonologiske ferdigheter.

Mulige linker mellom fonologiske evner og matematisk kompetanse understøttes ytterligere av studier som har identifisert tre hoveddimensjoner i fonologisk mangelfullhet («deficits»). Det er dårlig utviklet verbalt korttidsminne, langsom fremhenting av informasjon (retrieval) fra langtidsminnet og dårlig utviklet fonologisk bevissthet (Hecht et. al, 2001; Wagner & Torgesen, 1987). Svake prestasjoner i matematikk (matematikkvansker) kan forklares ved hjelp av en eller flere av de tre forannevnte dimensjonene. Ifølge Ranus og Szenkovits (2008) impliserer alle hver på sin måte fonologisk prosessering i matematikk. (For flere detaljer, se Ostad, 2010).

For øvrig har empiriske studier dokumentert statistisk signifikant korrelasjon mellom elevenes prestasjoner på verbalt korttidsminne, fonologisk bevissthet og rask prosesseringstid/retrieval (Hecht et al., 2001). Derfor har flere forskere argumentert med at alle typer oppgaver som måler fonologisk prosesseringsevne, kan ta utgangspunkt i en felles kjerne, en variabel («a core phonological processing variable») som angir styrken (funksjonaliteten) i den fonologiske prosesseringen (Snowling, 2001; Vellutino, Fletcher, Snowling & Scalon, 2004). Mot denne bakgrunn er det åpenbart av stor interesse å få kartlagt hvilke relasjoner som gjør seg gjeldende mellom privat taleinternalisering og fonologisk prosessering. Det er allerede påvist statistisk signifikant korrelasjon mellom indre tale og elevers bruk av retrieval-strategier under oppgaveløsningen (Ostad & Sorensen, 2007).

I den foreliggende artikkelen blir privat taleinternalisering under oppgaveløsning i matematikk fokusert, mens oppmerksomhet samtidig rettes mot fonologisk bevissthet.

Fonologisk bevissthet

Definisjonen av fonologisk bevissthet er omdiskutert. Men generelt kan uttrykket defineres som det å bevisst rette oppmerksomheten mot byggesteinene i språket, nærmere bestemt mot talespråkets lydmessige (fonologiske) struktur. I psykologisk forstand dreier det seg om elevenes evne til å analysere lydstrukturer i talespråket (Krajewski & Schneider, 2009).

Slik uttrykket blir brukt i faglitteraturen, ligger ferdighet i fonologisk bevissthet innenfor rammen av et kontinuum av kompleksitet. Når forskere skal forklare hva fonologisk bevissthet er, inkluderes ofte bevissthet om språklyder (fonem), stavelser og rim/rytme. (For grundig gjennomgang av definisjoner, se Snow, Burns, & Griffin, 1998). Utgangspunktet for den foreliggende artikkelen er et vidt syn på fonologisk bevissthet. I den empiriske delen av artikkelen omfatter fonologisk bevissthet evnen til å identifisere eller manipulere enheter i ord, nærmere bestemt lydmessig (fonologisk) struktur i tallnavn.

Innenfor leseforskningen har neppe noe annet tema oppnådd så mye oppmerksomhet i de senere år som fonologisk bevissthet. Det er vel kjent at fonologisk bevissthet påvirker leseog skriveutviklingen. Til sammenligning er relasjonen til matematisk kompetanse ikke så grundig studert (Krajewski & Schneider, 2009), men majoriteten av de (relativt få) empiriske studiene som i dag foreligger, synes å ha dokumentert at også matematisk kompetanse er influert av fonologisk bevissthet (Hecht et al., 2001; Simmons & Singleton, 2008). Men hvorfor og hvordan? Forskning spesielt rettet mot kausalitet ser imidlertid ut til å være høyst mangelfull og vil i tiden fremover stå overfor store utfordringer.

Den foreliggende undersøkelsen

En tidligere undersøkelse (Ostad & Sorensen, 2007) viste at det utviklingsnivået eleven har nådd i privat tale, er relatert til og spiller en sentral rolle for korrelasjonen til matematisk kompetanse. Her ble det påvist statistisk signifikante relasjoner mellom bruk av indre tale og bruk av retrievalstrategier. Undersøkelsen ga opphav til en ny, relativt optimistisk hypotese, nemlig at hensiktsmessig strategiutvikling (matematisk kompetanse) vil kunne fremstå som resultat av en systematisk stimulering av privat taleinternalisering. Med denne hypotesen som basis ble en relativt omfattende (50 ukers) intervensjon satt i verk (Ostad & Askeland, 2008). Ville et teoribasert undervisningsprogram, som er designet for å stimulere privat taleinternalisering, i seg selv gjøre elevene bedre i stand til å tilegne seg de aritmetiske basisenhetene, det vil si influere positivt på utviklingen av matematisk kompetanse? Her viste resultatene, det vil si gjennomsnittsresultat for alle elevene tatt under ett, signifikant positiv effekt av opplegget. Men da fokus ble rettet mot grupper av elever på ulike ferdighetsnivå i matematikk, viste det seg at den positive effekten av opplegget var minst, og ikke statistisk signifikant, i de gruppene som besto av de matematikksvake elevene. Dette resultatet la grunnlaget for en alternativ hypotese for videre forskning: Det er mekanismer (fonologiske prosesseringsevner) bak privat taleinternalisering og ikke privat taleinternalisering i seg selv som er kausalt relatert til matematisk kompetanse.

Det er verdt å merke seg at det tidligere ikke har foreligget empirisk forskning som eksplisitt retter oppmerksomheten mot den rolle fonologisk bevissthet har i privat taleinternalisering. Det var uventet å finne dette hulrommet i forskningen ettersom privat taleinternalisering har vist seg å predikere positivt hensiktsmessig strategibruk i faget (Ostad & Sorensen, 2007; Winsler & Naglieri, 2003).

Den foreliggende undersøkelsen er rettet spesielt mot de forannevnte svakhetene i forskningen. Generelt, og med henvisning til Vygotskys utviklingsperspektiv, som har vært rettesnor for de fleste undersøkelsene av barns private tale (for eksempel Berk, 1992; Winsler & Naglieri, 2003), var hovedhensikten her å tilføre den kognitive bakgrunnen for privat taleinternalisering i matematikk ny kunnskap. Mer spesifikt dreier undersøkelsen seg om (1) hvorvidt ferdigheter i fonologisk bevissthet er positivt relatert til privat taleinternalisering, og (2) hvorvidt svaret på spørsmålet foran varierer som funksjon av elevens alder og ferdighetsnivå i matematikk.

Metode

Design

Designet var bygd opp som en tverrsnittsundersøkelse. Tidligere undersøkelser hadde vist at elevers private tale blir influert av det som for øvrig foregår (kontekstuelle faktorer) i klasserommet (Berk, 1992; 0stad, 2007). Designet i den foreliggende undersøkelsen ble utviklet med prosedyrer for individuell observasjon utenfor klasserommet. Dette ble gjort for å sikre at de data som fremkom, ble registrert under best mulig sammenlignbare vilkår på tvers av elevers ferdighetsnivå i matematikk og klassetrinn.

Det ble gjennomført to separate observasjoner: Den ene for å kartlegge privat tale, den andre for å kartlegge fonologisk bevissthet. Den administrative rekkefølgen i de to observasjonene var basert på stratifisert utvelging («counterbalanced across subjects») innenfor rammen av de tre aldersgruppene som var inkludert.

Deltakerne

Som kontrollredskaper for elevenes matematikkunnskaper og læreforutsetninger ble henholdsvis «Basiskunnskaper i matematikk» (Hammervoll & Ostad, 1999) og komponenten «Arithmetic» i WISC-R (Undheim, 1977) benyttet. Ved hjelp av disse testene ble elevene med matematikkvansker (MD-elevene) valgt ut blant de elevene som tilfredsstilte begge de to følgende kriterier: (1) skulle oppnå stanine-skåre i intervallet 1–3 på matematikktesten, det vil si et resultat blant de 23 % svakeste resultatene i elevens aldersgruppe, og (2) skulle oppnå avledet skåre i intervallet 1–7 på komponenten «Arithmetic», dvs. et resultat blant de 25 % svakeste resultatene i sin aldersgruppe.

For å unngå «falske negativer» (Ostad, 2006, s. 29) ble elevene uten matematikkvansker (MN-elevene) valgt ut blant de flinkeste elevene. For hver aldersgruppe ble det valgt ut like mange gutter og jenter blant MN-elevene som det var gutter og jenter blant MD-elevene. Det endelige utvalget av MN-elever tilfredsstilte begge av de to følgende kriteriene: (1) skulle oppnå stanine-skåre i intervallet 7–9 på matematikktesten, dvs. et resultat blant de 23 % sterkeste i elevens aldersgruppe, og (2) oppnå avledet skåre 12–19 på komponenten «Arithmetic», dvs. et resultat blant de 25 % sterkeste resultatene i sin aldersgruppe.

Utvalget besto av i alt 134 elever. De kom fra 5 forskjellige grunnskoler i Hå kommune. Elevene tilhørte en av de følgende tre aldersgruppene (Agr): Agr 1: elever i 2. og 3. klasse, Agr 2: elever i 4. og 5. klasse, Agr 3: elever i 6. og 7. klasse.

Observasjonskategori: Privat tale

Det forelå på forhånd ikke noe enhetlig kategoriseringssystem av privat tale. Når kategoriseringssystemet til den foreliggende undersøkelsen skulle utvikles, ble ulike synspunkter fra tidligere undersøkelser forsøkt integrert (Berk, 1992; Girbau, 2002, Kolberg et al., 1968). For å oppnå dette ble enhetene i systemet definert med hensyn til internaliseringsgrad av privat tale og inkluderte (a) ytre verbal produksjon ved hjelp av ord og språklyder, (b) ytre manifestasjon av tilsvarende («appropriate») privat tale og (c) privat tale i stillhet (Girbau, 2002).

(a) Privat tale (høy, normal eller lav) skal være hørbar slik at utsagnene kan være forståelige og derfor kan bli transkribert. (b) Privat tale skal være uhørlig og uforståelig, men likevel observerbar under «face-to-face»-observasjon (for eksempel uhørlig mumling eller leppeog tungebevegelse). Det er bredt akseptert blant forskere at privat tale innenfor rammen av denne enheten representerer ytre manifestasjon av indre tale (Berk, 1992; Kolberg et al., 1968). De klassifikasjonssystemene som hadde vært benyttet i tidligere forskning, (Berk, 1992; Kolberg et al., 1968) hadde vanligvis brukt kategorien ytre manifestasjon av ytre tale som det høyeste nivået i internaliseringsprosessen. (c) Undersøkelser har imidlertid vist at privat tale kan være subvokal, det vil si foregå i stillhet uten noen form for ytre verbal produksjon eller uhørlig manifestasjon (Girbau, 2002). I den foreliggende undersøkelsen blir subvokal tale definert som rene implisitte, skjulte mentale prosesser som ikke er observerbare under «face-to-face» observasjon. Innenfor det valgte kategoriseringssystem (pkt. a, b og c) syntes det rimelig å betrakte subvokal tale som det høyeste nivået i internaliseringen av privat tale. I samsvar med de alternativene som er beskrevet ovenfor, ble de tre kategoriene kodet som hørlig privat tale («Aud»), uhørlig privat tale («Inaud») og privat tale i stillhet («Sil»).

Observasjonskategori: Fonologisk bevissthet

Tidligere undersøkelser av fonologisk bevissthet har ikke brukt målemidler som var utviklet spesifikt med tanke på matematikkfaget. Den relativt omfattende forskningslitteraturen innenfor lesning og skriving (for eksempel Adams, Foorman, Lundberg & Beeler, 1998; Hecht et al., 2001) har imidlertid bidratt med kunnskaper som ser ut til å kunne overføres til andre fagområder. Den testen som ble utviklet for måling av fonologisk bevissthet i den foreliggende undersøkelsen, ble derfor utformet etter mønster fra leseog skriveforskningen.

Testen tok utgangspunkt i 15 tallnavn (2-, 3, og 4-sifrede) arrangert i rekkefølge etter vanskegrad. Til hvert tallnavn var det fire oppgaver relatert til henholdsvis «blending», «analysis», «delection» og «substitution». Eksemplet som følger tar utgangspunkt i tallet «795»:

Blending: Testlederen sier de enkelte sifrene i tallet (det egentlige tallnavnet) til eleven, og eleven blir instruert til å trekke sammen fonemene (enkeltsifrene) til tallet (for eksempel /7, /9/ og /5/ til /795/).

Analysis: Testlederen sier tallnavnet til eleven, og eleven blir instruert til å si sifrene i tallnavnet i samme rekkefølge som eleven hører dem (for eksempel: «Si sifrene du hører i tallet /795/ i samme rekkefølge som du hører dem»).

Deletion: Eleven blir instruert til å si tallnavnet som fremkommer når siffer i begynnelsen, midten eller som slutt i et tallnavn blir utelatt (for eksempel: «Si hvilket tall du får hvis du fjerner /9/ i tallet /795/»).

Substitution: Eleven blir instruert i å si tallnavnet som fremkommer når et spesifikt siffer blir erstattet av et annet (for eksempel: «Si hvilket tall du får om du bytter /9/ med /3/ i tallet /795/»).

De oppgavetypene som krever manipulering av fonemer, synes å være de vanskeligste. Hvordan oppgavetypene relaterer til hverandre, har forskningslitteraturen ikke gitt noe endelig svar på (Adams et al., 1998; Hecht et al., 2001). Den foreliggende testen gir derfor ikke rom for sammenligninger av resultatene på de enkelte komponentene i testen, men er basert på den antagelse at de ulike komponentene reflekterer en enkel latent evne (Anatony & Francis, 2005) og at denne er endimensjonal (Hambleton et al., 1991).

Observasjonsprosedyre: Testen ble administrert individuelt, og fire oppgaver ble gitt som førtrening (med nødvendig feedback) for å unngå misforståelser. Oppgavene (de 15) ble vektet basert på relativ vanskegrad med for-holdstallene 1: 2: 3 for henholdsvis 2-, 3- og 4-sifrede tall. Deltakerne fikk poeng for riktig oppgave når det forelå tilfredsstillende svar på alle de fire komponentene. Testingen ble avsluttet etter to påfølgende gale svar.

Resultatet viste at ingen av deltakerne hadde avgitt gale svar på noen av de oppgavene som knyttet seg til «blending» eller «analysis». På denne bakgrunn ble det besluttet bare å benytte de poengene elevene hadde samlet i «deletion» og «substitution» som data for de statistiske analysene. Det totale antall poeng (maksimum 32 poeng) ble tranformert til avledede skårer («scaled scores»). Avhengig av testresultatet tilhørte eleven ett av de tre ferdighetsnivåene i fonologisk bevissthet: lav (LavPh), medium (MedPh) eller høy (HøyPh). De tre nivåene inkluderte elever med avledede skårer i intervallene 1–8, 9–14 eller 15–20.

Resultater i hovedtrekk

De resultatene som viser utviklingen av privat tale blant elever med og uten matematikkvansker, er presentert i en tidligere publikasjon og vil ikke bli gjentatt her (se Ostad, 2007).

I den foreliggende undersøkelsen ble oppmerksomheten rettet mot fonologisk bevissthet blant elever med og uten matematikkvansker. Figur 1 gir en oversikt over resultatene slik de fremkommer som funksjon av elevenes alder og de tre definerte ferdighetsnivåene av fonologisk bevissthet (LavPh, MedPh og HøyPh).

Merk: MD = elever med matematikkvansker. MN = elever uten matematikkvansker; Agr1 = aldersgruppe 1 (2. og 3. klasse); Agr2 = aldersgruppe 2 (4. og 5. klasse); Agr3 = aldersgruppe 3 (6. og 7. klasse).

Figur 1, som her gjenspeiler utviklingen av fonologisk bevissthet, dokumenterer et påfallende forskjellig utviklingsmønster blant elever med og uten matematikkvansker. For elever med matematikkvansker stagnerer utviklingen i tidlig alder. Elevene uten matematikkvansker derimot viser opp gjennom grunnskolealderen en markert og aldersrelatert fremgang fra lavere til høyere ferdighetsnivå. Forskjellene mellom elevene med og uten matematikkvansker er statistisk signifikant i alle (de tre) aldersgruppene.

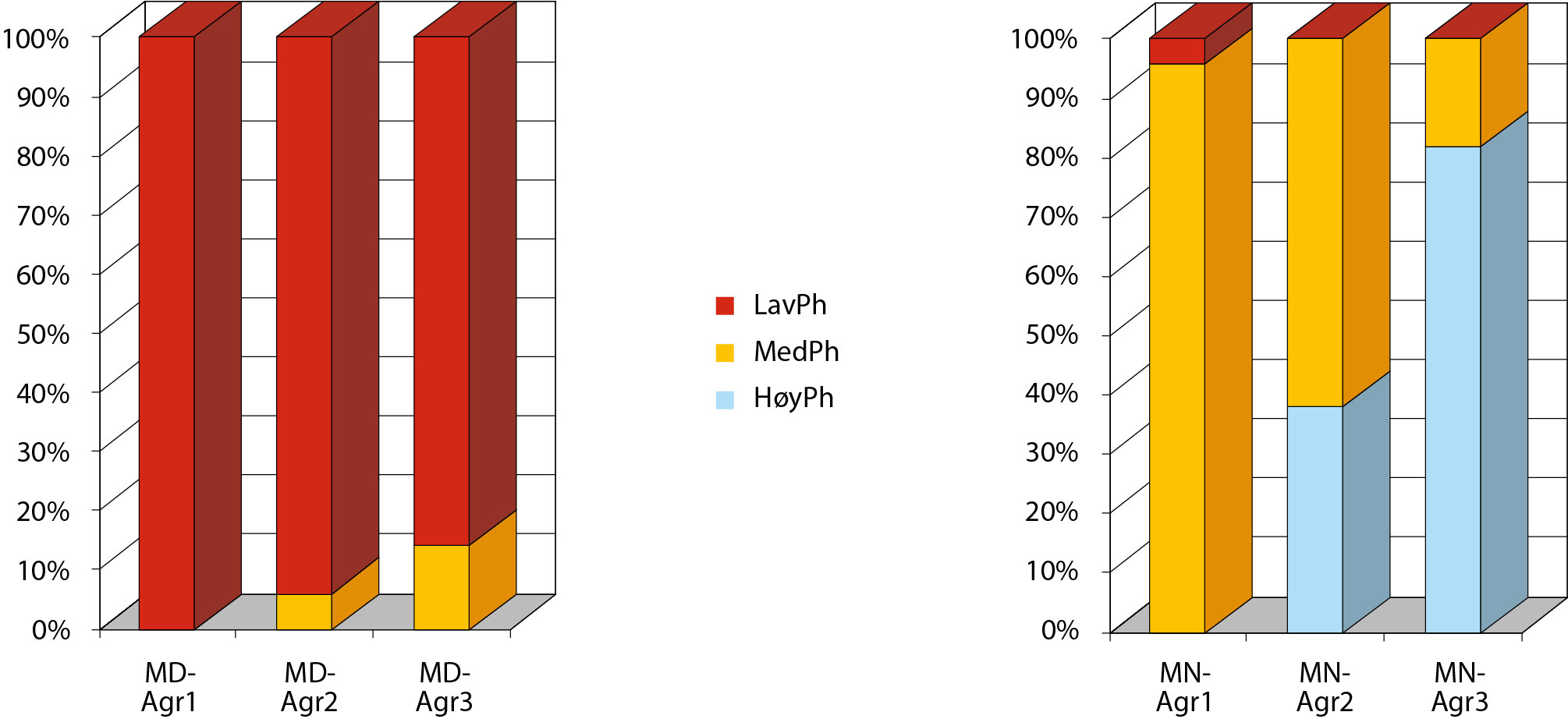
Resultatene fra den foreliggende undersøkelse synes dermed å bekrefte tidligere undersøkelser som taler for at mål for ferdighet i fonologisk bevissthet vil kunne fungere som et relevant redskap til å forutsi elevenes matematikkfaglige utvikling i skolen (Hecht et al., 2001; Ramus & Szenkovits, 2008). Resultatene synes derfor også å støtte opp under «phonological deficit theory» (Wagner & Torgesen, 1987) der det hevdes at unge elever med lavt ferdighetsnivå («low/imparied») i fonologisk bevissthet befinner seg i en risikosone for å utvikle matematikkvansker.

Innenfor rammen av den foreliggende undersøkelsen er sannsynligvis det mest originale forskningsarbeidet knyttet til relasjonen mellom ferdighet i fonologisk bevissthet og privat taleinternalisering. Her blir den nevnte relasjonen observert og analysert i et longitudinelt perspektiv samtidig som fokus rettes mot elever med og uten matematikkvansker. Figur 2, 3 og 4 angir i prosent forekomsten av de aktuelle kategorikombinasjonene som fremkom mellom privat tale og fonologisk bevissthet.

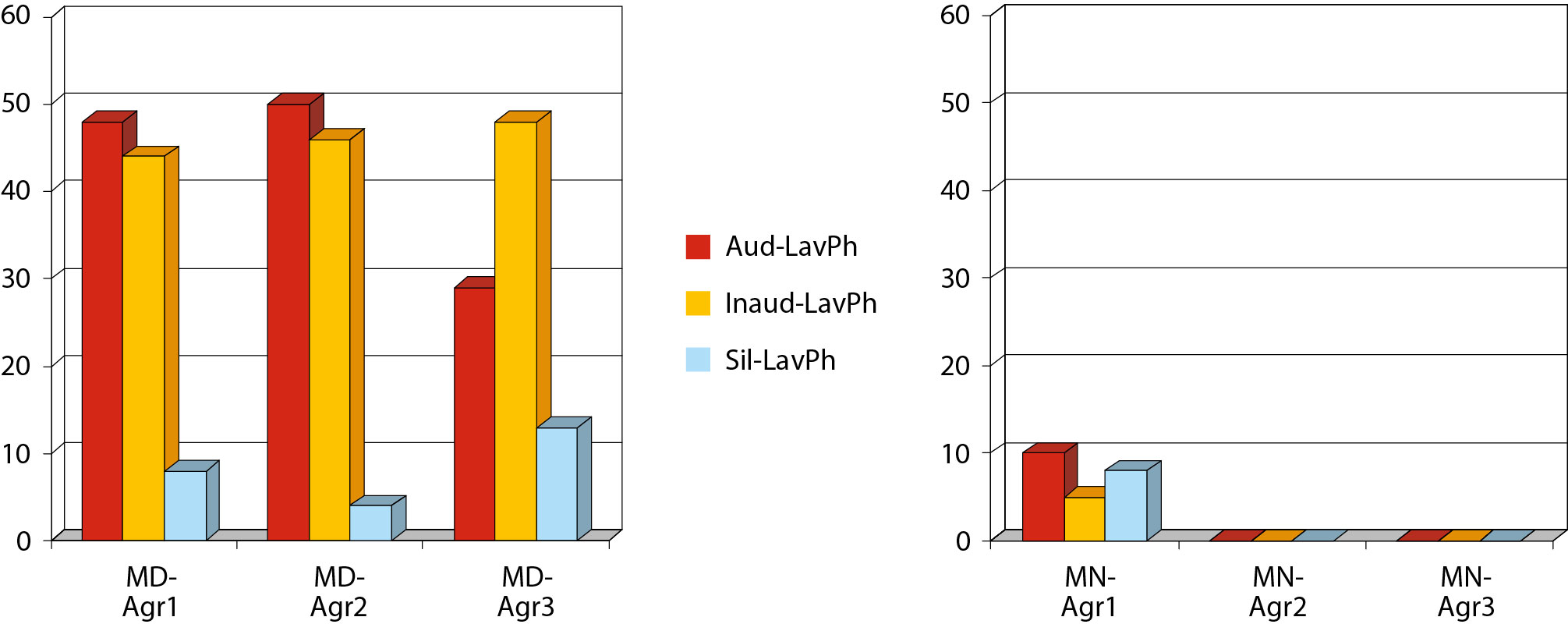
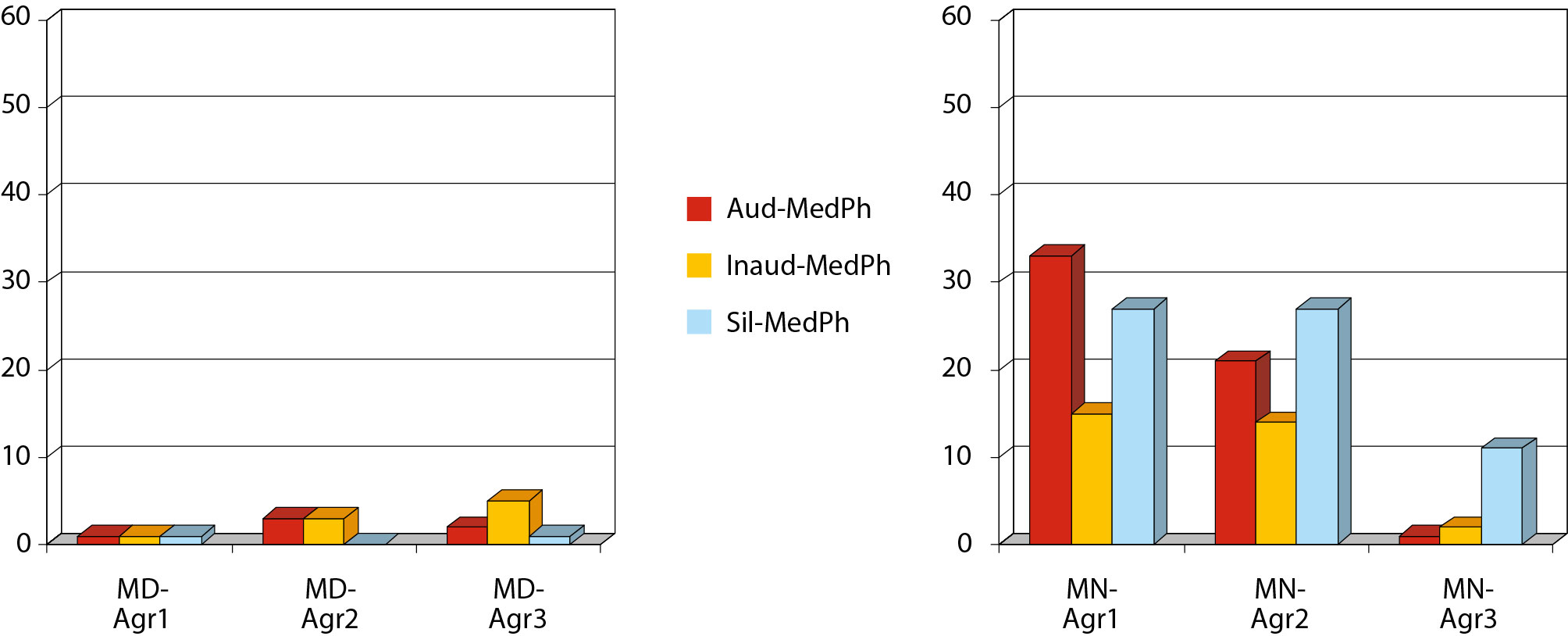
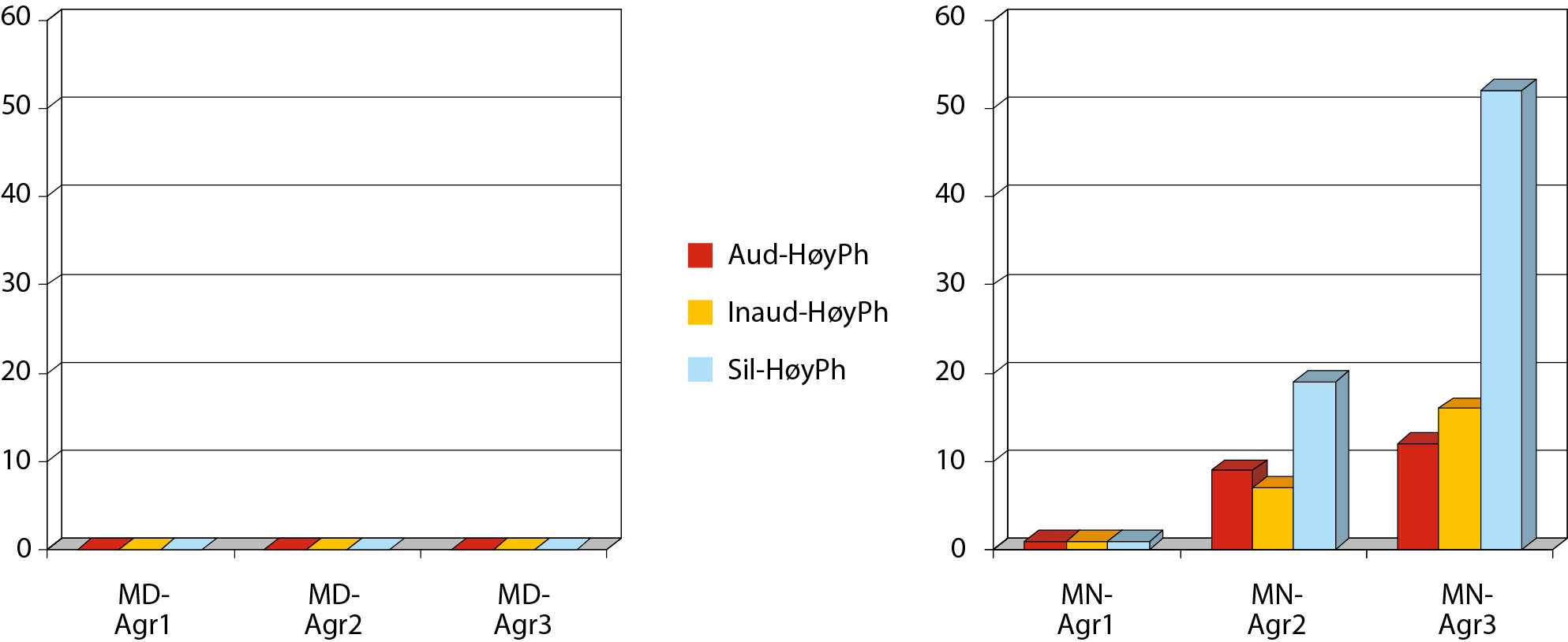
Merk: For Figur 2–4 gjelder følgende: MD = elever med matematikkvansker. MN = elever uten matematikkvansker; Agr1 = aldersgruppe 1 (2. og 3. klasse); Agr2 = aldersgruppe 2 (4. og 5. klasse); Agr3 = aldersgruppe 3 (6. og 7. klasse).

For elever med matematikkvansker fremkom det opp gjennom grunnskolealderen et utviklingsmønster ikke bare karakterisert med lavt ferdighetsnivå i fonologisk bevissthet, men også med langt oftere bruk av de laveste nivåene i privat taleinternalisering. De typiske elevene i denne gruppe så ut til å oppholde seg i kombinasjonen uhørlig privat tale/ lavt nivå i fonologisk bevissthet.

Det karakteristiske utviklingsmønsteret for elever uten matematikkvansker kjennetegnes derimot ved en aldersrelatert utvikling fra hørlig privat tale til privat tale i stillhet og fra lavere til høyere ferdighetsnivå av fonologisk bevissthet.

Den mest markerte forskjellen mellom elever med og uten matematikkvansker er relatert til kombinasjonen privat tale i stillhet/høyt ferdighetsnivå i fonologisk bevissthet. Undersøkelsen viste at elever uten matematikkvansker benyttet denne kombinasjonen langt oftere enn elever med matematikkvansker. Forskjellen mellom de to gruppene ble tydeligere og tydeligere opp gjennom grunnskolealderen.

Drøfting

Generelt representerer den foreliggende undersøkelsen et bidrag til ytterligere å synliggjøre relevansen i forskning som retter fokus mot relasjoner mellom privat taleinternalisering og matematisk kompetanse. Samtidig, og i et nytt perspektiv, vil resultatene også henlede oppmerksomheten mot en mulig parallell rolle til utviklingen av fonologisk bevissthet. Det hører med til historien at statistiske analyser av data fra den foreliggende undersøkelse (Ostad, in press) dokumenterer statistisk signifikant korrelasjon mellom elevenes utviklingsnivå når det gjelder privat tale og fonologisk bevissthet. Et viktig spørsmål er derfor hvorfor de to dimensjonene, det vil si utvikling av privat tale og fonologisk bevissthet, griper inn i hverandre slik undersøkelsen indikerer.

Det foreligger i dag ingen enkel forklaring på dette spørsmålet. Matematisk kompetanse, inkludert tilkortkomming i faget, har vært gjenstand for studier fra ulike faglige perspektiver (Geary, 1993). Det kunne for eksempel tenkes at det virkelig eksisterer et gjensidig («reciprocal») relasjonssystem som regulerer forholdet mellom matematikk, privat tale og fonologisk bevissthet. Et slikt «system» kunne som ett mulig alternativ forklare hvorfor korrelasjonen mellom privat tale og fonologisk bevissthet ble dokumentert som statistisk signifikant resultat i undersøkelsen. Resultater fra tidligere forskning (Wagner & Torgesen, 1987) har indikert at både privat tale og fonologisk bevissthet er støttet opp av («underpinned by») fonologiske ferdigheter som er avhengig av kvaliteten på det lydbaserte kunnskapslageret («phonological representations»).

Ettersom barn med matematikkvansker sammenlignet med barn uten matematikkvansker la for dagen langt mindre bruk av de mest internaliserte privat tale kategoriene, vil en alternativ forklaring være at elevenes ferdighetsnivå i fonologisk bevissthet er en funksjon av deres utvikling av privat tale.

Interessant nok viser undersøkelsen at relasjonen mellom privat tale og fonologisk bevissthet er langt svakere blant elever med enn blant elever uten matematikkvansker (Ostad, in press). Dette resultatet åpner opp for en tredje alternativ forklaring, nemlig om forsinket utvikling av fonologisk bevissthet forårsaker forsinket utvikling av privat tale. Hvis dette alternativet er valid, ville det, i hvert fall delvis, kunne forklare hvorfor systematisk trening rettet mot utvikling av privat tale ikke hadde forventet positiv effekt på utviklingen av matematisk kompetanse blant elevene med matematikkvansker (Ostad & Askeland, 2008).

Videre arbeid måtte forsøke å avdekke hvorvidt systematisk stimulering av fonologisk bevissthet kan influere positivt på utviklingen av privat tale og matematisk kompetanse. Hvordan bør slik stimulering foregå innenfor rammen av matematikkfaget? Her er det grunn til å etterlyse nye intervensjonsstudier.

Etterord

Data fra undersøkelsen blir også publisert som forskningsartikkel i «Journal of Learning Disabilities», der i en langt mer omfattende form med bredere teoretisk forankring og langt mer detaljert datapresentasjon og statistiske analyser. Tittel er: «Phonological awareness in arithmetical calculation: Its relation to private speech internalization in children with and without mathematical difficulties» (Ostad, in press).