Algebra og tall er motoren i matematikken – derfor går matematikkfaget i Norden for halv fart

Denne artikkelen tar opp matematikk i skolen med vekt på utviklingen i prestasjoner i TIMSS 2011 i Norge, Sverige og Finland. Norge og Sverige hadde en markert nedgang i prestasjoner fra 1995 til 2003. Finland har en tilsvarende markert nedgang i prestasjoner fra 1999 til 2011. Etter 2003 har TIMSS to ganger målt framgang i norske elevers prestasjoner i matematikk, mens man to ganger har målt tilbakegang i svenske elevers prestasjoner. Men felles for alle tre land er at de presterer svakt i algebra. Algebra er sammen med tall motoren i matematikken. Algebra er en generalisering av regning med tall, og et kraftfullt verktøy for all videre læring og bruk av matematikk.

Algebra i Norge, Sverige og Finland

Figur 1 viser prestasjoner på de ulike fagområdene i matematikk for de tre nordiske landene som deltok på ungdomstrinnet i TIMSS 2011, Norge, Sverige og Finland. Alle de nordiske landene presterer svakt i algebra. De norske elevenes prestasjoner er aller svakest, men her må vi ta med i vurderingen at de norske elevene er ett år yngre enn elevene i Sverige og Finland. Ser vi på land utenfor Norden i figur 1 (høyre side i figuren), presterer de japanske elevene høyt på alle områdene, og for eksempel klart bedre i algebra enn i tall. Selv om de italienske og slovenske elevene presterer noe svakere i algebra enn på andre områder, er ikke dette like markert som det er for elevene i de nordiske landene.

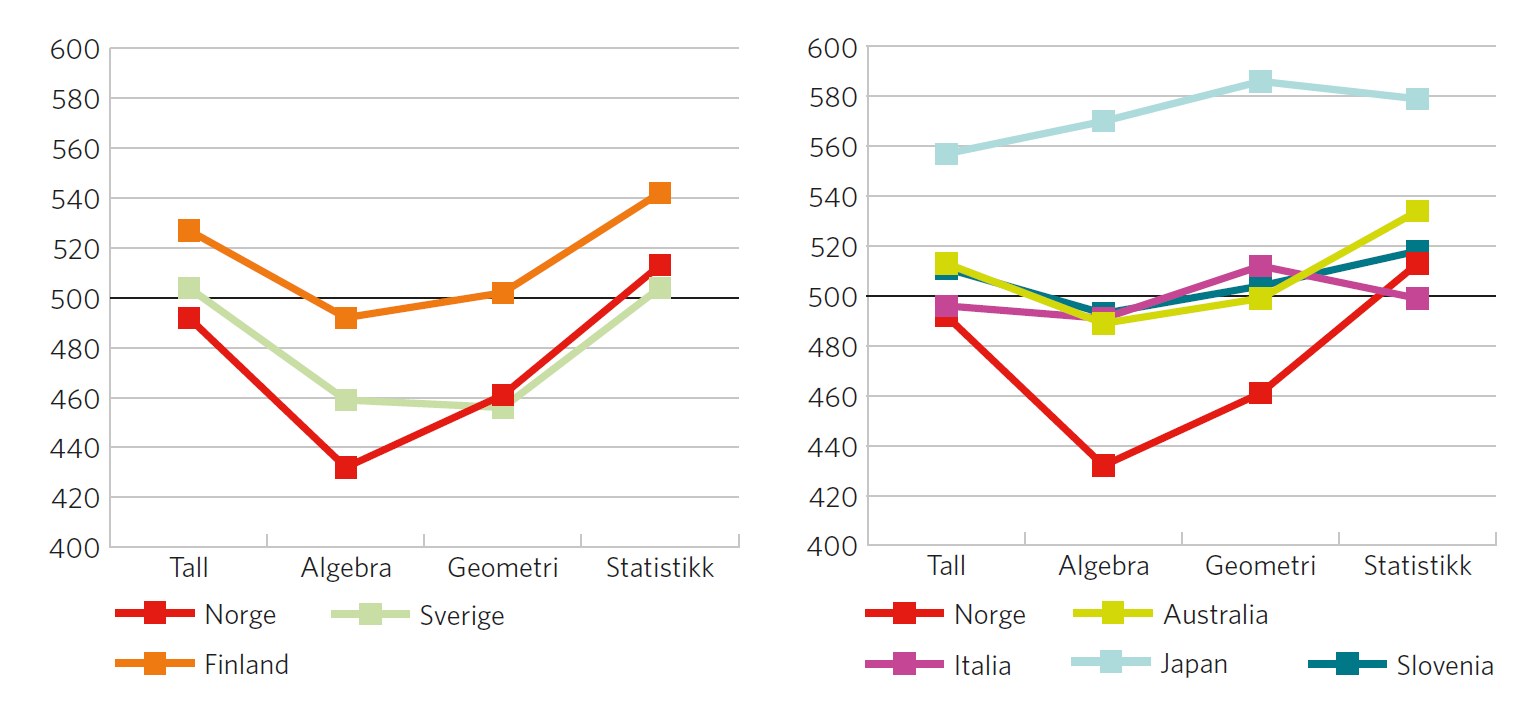
Tilbakegang og framgang på ungdomstrinnet i nordiske land

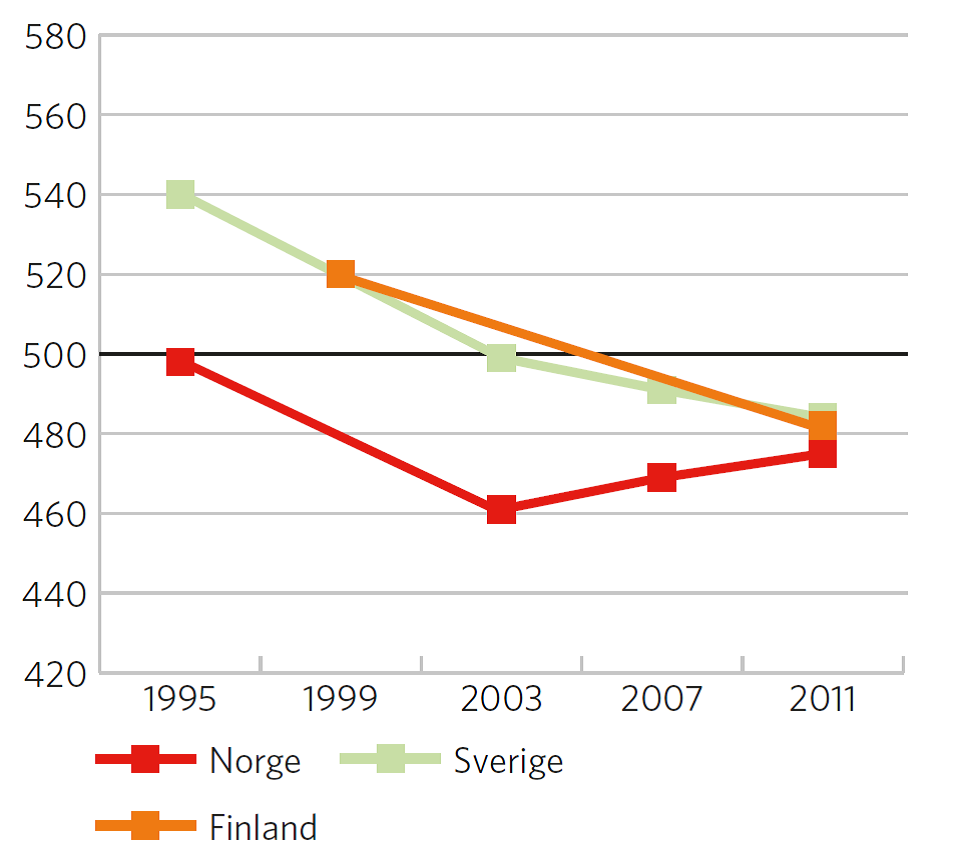
Figur 2 viser utviklingen i matematikkprestasjoner for Norge, Sverige og Finland. Som det framgår av figuren, er det særlig for Norge og Sverige på 8. trinn at vi har målinger fra flere år. Norge og Sverige hadde samme negative utvikling fra 1995 til 2003, men utvikler seg ganske ulikt fra 2003 til 2011. I Sverige fortsetter den negative utviklingen i elevprestasjoner, mens Norge har en positiv utvikling i elevprestasjoner fra 2003 til 2011. Figur 2 viser også at Finland, som tidligere bare har deltatt i 1999 (TIMSS repeat) og nå i 2011, har en markant nedgang i denne perioden. De finske elevene som det måles en markert nedgang for fra 1999 til 2011, går på 7. trinn, men er jevngamle med de norske elevene på 8. trinn. Finland testet elevene både på 7. trinn og på 8. trinn i TIMSS 2011. For mer om problematikken rundt ulik alder og trinn på elevene, se Grønmo et. al (2012). Det er problematisk å gjøre direkte sammenlikninger fordi Finland og de andre nordiske landene definerer opplæringstilbudet til 6-åringer som førskole, mens tilbudet til 6-åringer i Norge defineres som skole. I TIMSS 2011 presterer jevngamle elever i Finland bare marginalt bedre enn de norske elevene, 7 poeng bedre av et standardavvik på 100.

Nedgangen i matematikkprestasjoner fra 1999 til 2011 for Finland er på samme nivå som nedgangen for Norge og Sverige fra 1995 til 2003, det vil si cirka 40 poeng. De svenske elevene i figur 2 er ett år eldre enn både de norske og de finske elevene. Tar man hensyn til ulik alder på elevene, presterer svenske elever i TIMSS 2011 svakere enn elever både i Finland og i Norge.

Når det gjelder Finlands tilbakegang, advarte over 200 finske matematikere og matematikkdidaktikere allerede i 2005 om at finske elevers prestasjoner i matematikk ikke var så gode som deres resultater i PISA kunne tyde på (Astala et. al, 2005). De hevdet blant annet at det var et problem at finske elever ikke lærte ren, abstrakt matematikk som for eksempel algebra, fordi nesten alt fokus var på såkalt «hverdagsmatematikk». Tidligere norske TIMSS-rapporter (Grønmo et. al, 2004, Grønmo & Onstad, 2009) har pekt på det samme som et problem i norsk matematikkundervisning. På tross av Finlands oppsiktsvekkende gode resultater i PISA, advarte altså finske matematikere for åtte år siden mot en utvikling som i liten grad gir elevene den type matematikkunnskaper som mange av dem trenger i videre utdanning og profesjoner.

En nordisk profil for matematikk i skolen

Analyser av data fra flere tidligere TIMSS- og PISA-studier har vist at man finner relativt stabile grupper av land, over tid og i ulike studier, som har det vi kan kalle en felles profil for hva de relativt sett legger mest vekt på i matematikkundervisningen i skolen. Basert på analyser av hvilke land som ser ut til å legge relativt mest vekt på de samme fagområdene i matematikk, kan vi snakke om en nordisk profil, en engelskspråklig profil, en østeuropeisk profil og en østasiatisk profil. Disse fire profilene kan man igjen dele opp i to typer profiler, en type med relativt mest vekt på dagliglivsmatematikk, som den nordiske og den engelskspråklige profilen, og en type som legger relativt mest vekt på ren abstrakt matematikk, som den østeuropeiske og den østasiatiske profilen. (For mer om ulike profiler i matematikk i skolen se Grønmo (2010), Grønmo & Onstad (2013), Grønmo, Kjærnsli og Lie (2004), Grønmo & Olsen, 2006, Olsen og Grønmo, 2006).

Det som karakteriserer den nordiske profilen, er nettopp det de finske matematikerne advarte mot i 2005, for ensidig vekt på anvendt matematikk i dagliglivet, og for lite vekt på ren matematikk som algebra. Er det slik at en altfor ensidig vekt på anvendt dagliglivsmatematikk er en viktig årsak til den markerte nedgangen i norske og svenske elevers prestasjoner fra 1995 til 2003, og til den tilsvarende markerte nedgangen i finske elevers prestasjoner fra 1999 til 2011? Resultatene på de ulike fagområdene i matematikk som er presentert i figur 1, og tidligere analyser av hva som kjennetegner en nordisk profil i faget, kan tyde på det.

Forskere har pekt på at endringer i læreplaner i en del land har vært drevet av et ønske om å legge større vekt på dagliglivsmatematikk på bekostning av mer abstrakt matematikk som for eksempel algebra (Mosvold, 2010, Gardiner, 2004). Problemet med dette er at mange elever trenger for eksempel algebra for videreutdanning og profesjoner. For mer om tendensen til å legge mer vekt på dagliglivsmatematikk, se for eksempel De Lange (1996), Kilpatrick, Hoyles, Skovsmose og Valero (2005). I den norske læreplanen fram til 2006, var «Matematikk i dagliglivet» det første av fagets fem målområder, og der sto det også at dette skal være et gjennomgående tema for å gi «faget en sosial og kulturell forankring og skal særlig ivareta det brukerorienterte aspektet» (L97, s. 156). Det er grunn til å problematisere at det «brukerorienterte aspektet» som nevnes i læreplanen, i stor grad ble fortolket som dagliglivsmatematikk. Matematikk som bruksredskap er minst like viktig for mange elever som skal inn i ulike yrker og profesjoner hvor de trenger matematikk. For eksempel gjelder det ingeniørfag, økonomifag, datakunnskap og naturvitenskapelige fag.

Et av problemene ved stor vekt på anvendt matematikk i dagliglivet, og liten vekt på ren matematikk, kan illustreres ved å ta utgangspunkt i en allment akseptert modell for forholdet mellom ren og anvendt matematikk fra Standards i USA (National Council of Teachers of Mathematics, 1989).

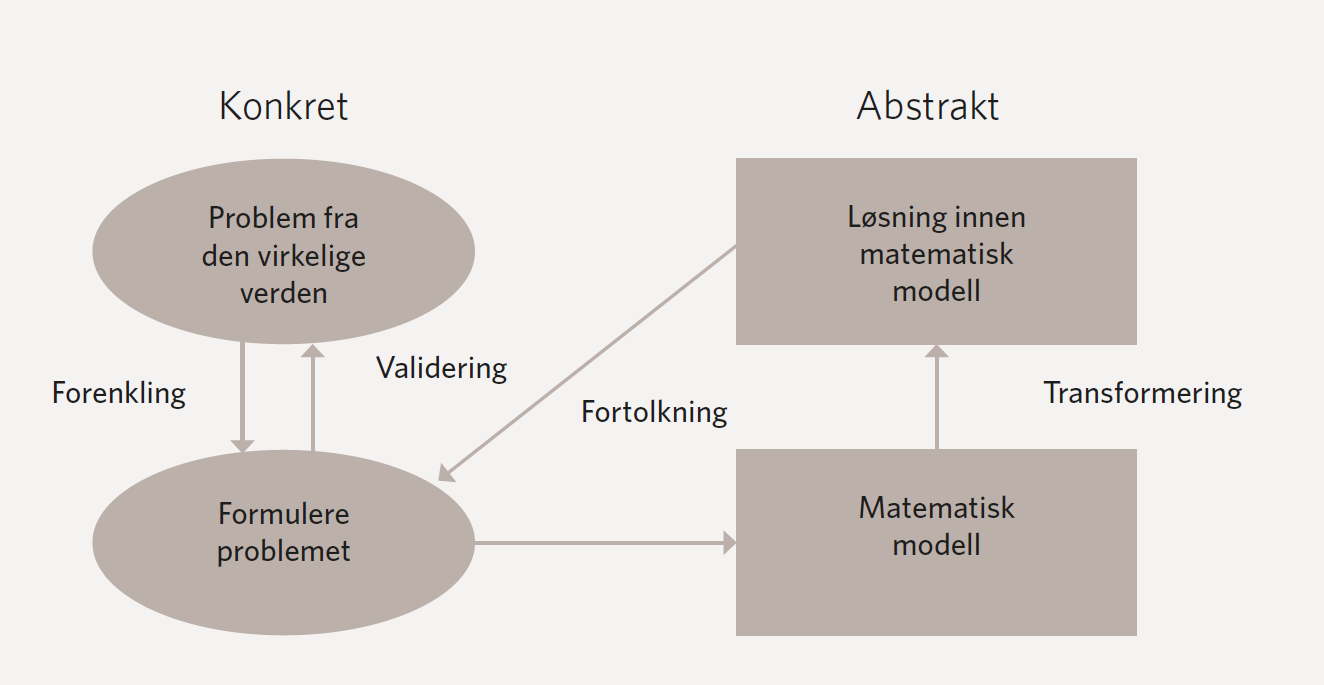
PISA bruker en innholdsmessig lik modell som er litt annerledes utformet (OECD, 2003, p. 38).

Høyre side av figuren viser den matematiske verden, en egen abstrakt verden med veldefinerte symboler og regler. Venstre side forestiller den virkelige, konkrete verden som omgir oss. Ren matematikk, som arbeid med tall og algebra uten å knytte det til problemer fra virkeligheten, vil bare foregå på høyre side på figuren. Man bruker da gjerne betegnelser som matematisk uttrykk om det man arbeider med. Å beregne svaret på et addisjons- eller multiplikasjonsstykke eller å finne ut hva som passer i en algebraisk likning, er eksempler på arbeid innen ren matematikk. I anvendt matematikk tar man utgangspunkt i et problem fra den virkelige verden. Man må da først gjøre en forenkling og formulere problemet klart, så skal dette matematiseres og ende i en matematisk modell. Deretter arbeider man innen den rene matematiske verden med en transformasjon av den matematiske modellen.

Hvis man arbeider med tallsymboler, kan det for eksempel være å foreta en utregning, i algebra kan det være en manipulering med bokstavsymboler. Løsningen man kommer fram til, må være riktig i forhold til de regler som gjelder innen den matematiske verden. Så skal løsningen relateres tilbake til den virkelige verden gjennom en fortolkning av hva dette innebærer i forhold til det formulerte problemet. Til slutt skal rimeligheten av svaret valideres i forhold til det opprinnelige problemet. Anvendelse av matematikk forutsetter derfor både at man kan orientere seg med en rimelig sikkerhet i den rene matematiske verden, og at man med utgangspunkt i en virkelig problemstilling kan matematisere og sette opp en modell som man arbeider med, for til slutt å relatere svaret tilbake til problemet i den virkelige verden. Anvendt matematikk er derfor i sin natur kompleks, og forutsetter gode kunnskaper i ren matematikk.

Arbeid innen ren matematikk som utregninger, omforming og manipulering med matematiske symboler har tradisjonelt hatt en sterk posisjon i skolematematikk. I dette matematiske universet er matematikk en sikker, presis og eksakt vitenskap, hvor teorier og teser kan bevises eller motbevises. I det øyeblikk vi forbinder matematikk med virkeligheten, er ikke matematikk mer presis enn andre typer vitenskap. Enhver anvendelse er forbundet med usikkerhet. Albert Einstein har uttalt at

As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality (Humboldt 2004).

Med økt vekt på anvendelse av matematikk kan det synes som om betydningen av å lære ren matematikk, og å forstå at ren matematikk er en eksakt og sikker vitenskap, i noen grad har forsvunnet fra skolematematikken (Gardiner 2004). Formuleringer som «bare en manipulering med symboler» er blitt brukt om matematikk som «bare» opererer på figurens høyre side. Arbeid innen ren matematikk forutsetter i høyeste grad refleksjon og forståelse, men da innen den matematiske verden. Dette kan for eksempel være refleksjon rundt sammenhengen mellom addisjon og multiplikasjon eller forståelse av brøk og desimaltall som ulike representasjonsformer. Eller det kan være refleksjon og forståelse av ulike representasjonsformer for funksjoner, som en algebraisk likning, en grafisk framstilling, en tabell eller en beskrivende tekst. Å forstå og gi mening til ren matematikk er i seg selv en stor utfordring. Det gjelder på områdene tall og tallregning, som nok er den delen av matematikken som anvendes mest i dagliglivet. Og det gjelder på et område som algebra, som mange elever trenger for videreutdanning og profesjoner.

Det synes uproblematisk å akseptere at et viktig mål for undervisningen i skolen er at elevene skal kunne anvende matematikk, både i dagligliv og i yrkesliv. Det problematiske er hvis dette oppfattes som et alternativ til tradisjonell matematikkundervisning (Gardiner, 2004). Stiller vi spørsmålet om hva som skal være innholdet i en undervisning for å fremme anvendelse av matematikk på problemer i dagliglivet, eller i videreutdanning og senere yrker, er det ikke sikkert at vi ender opp med så mye nytt (ibid., 2004). For å kunne anvende matematikk må man ha en rimelig god kompetanse med grunnleggende faglige fakta, ferdigheter og begreper i faget. Uten dette grunnlaget har man lite å anvende. Den faglige basisen kommer vi ikke utenom, selv om vi vet at mange må slite for å skaffe seg denne.

Den rene abstrakte matematikken som det er viktigst at elevene tilegner seg, er på områdene tall og algebra, det vi kan kalle motoren i matematikken. Gode kunnskaper i tall og tallregning trenger alle, men en stor del av befolkningen trenger også gode grunnleggende kunnskaper i algebra. Det er det de trenger i mange videreutdanninger og profesjoner, for å bli ingeniører eller økonomer, eller innen datakunnskap, naturvitenskap og matematikk. Matematikk for alle har vært et populært slagord i Norge, som i mange andre land. Men å fortolke det som den matematikken alle trenger i dagliglivet, er en snever fortolkning. En mer rimelig fortolkning synes å være at i grunnskolen skal alle få grunnleggende kunnskaper i den typen matematikk de vil trenge, enten i dagligliv eller i videre utdanning eller yrkesliv. Da kommer man ikke utenom grunnleggende kunnskaper i algebra.

Basisferdigheter i algebra

For elevene i grunnskolen ser det ut til at det særlig er det vi kan kalle basisferdigheter i algebra som har blitt forsømt. Det har vært mange ulike tiltak og kampanjer for å rekruttere elever til realfaglige utdanninger og profesjoner i Norge, men hvis ikke skolen legger opp til å gi elevene den basiskunnskapen de trenger for å gjennomføre slike studier, er dette nesten å lure elevene. Vi vet at hovedårsaken til frafall i mange studier, som ingeniørutdanninger, er at elevene mangler grunnleggende ferdigheter i algebra (NOKUT, 2008). Det er et samfunnsansvar å legge til rette for at elevene får denne typen kunnskap i skolen. Dette er viktig både for den enkelte elev og for samfunnet som trenger personer i denne typen yrker.

Det ser ut til at grunnskolen både i Norge, Sverige og Finland legger for stor vekt på anvendt matematikk i dagliglivet, og ikke tar på alvor ansvaret for å gi elevene de basisferdighetene i algebra som mange av dem vil trenge for videre utdanning og yrker.