Leseforståelse og matematikk

*Denne artikkelen bygger på følgende vitenskapelige produksjoner: (Nortvedt, 2009, 2010, 2011a)

Matematikk er et fag mange elever opplever som skremmende og mange har erfart nederlag når de skal løse oppgaver innenfor faget. Når elever sliter med matematikken, kan dette også ha med andre ferdigheter å gjøre enn det vi vanligvis tenker på som matematikk. Elevene leser også i matematikktimene, for eksempel når de løser tekstoppgaver. Men hva er egentlig en tekstoppgave?

Vi kan grovt dele matematikkoppgavene elevene møter i opplæringssituasjoner inn i to grupper: Oppstilte oppgaver der regnemåten er gitt og tekstoppgaver der elevene selv med utgangspunkt i teksten må finne frem til hvordan oppgaven kan løses. I skolens matematikkundervisning brukes tekstoppgaver med flere ulike formål. Dels brukes disse oppgavene for å øve på innøvde regneteknikker, dels for å øve på problemløsing og modellering og dels for å utforske matematiske sammenhenger når nytt stoff skal innlæres (Nortvedt, 2012). Uavhengig av hvilket av de tre formålene eller bruksområdene en lærer har når han eller hun gir elevene tekstoppgaver, må elevene lese og forstå teksten i oppgaven før den kan løses. Elevene trekker veksler på både matematisk kompetanse og generelle lesestrategier når de leser tekstoppgaver.

Å forstå en oppgave vil si at eleven gjennom lesingen danner seg en mental modell av det matematiske problemet som ligger innbakt i teksten. Denne mentale modellen inneholder elevens matematiske modell som eleven bruker når han eller hun løser oppgaven (Nortvedt, 2008). Elevens mentale matematiske modell kan inneholde den intenderte oppgave, men dersom eleven ikke har lykkes med å forstå teksten, vil elevens modell inneholde feil.

Oppgaver som inneholder skjult eller irrelevant informasjon, kan for eksempel være utfordrende. Deretter må eleven forme en plan, bevisst eller ubevisst, for hvordan oppgaven kan løses før han/hun gjennomfører de beregninger som er nødvendige (Verschaffel, De Corte, & Greer, 2000). Helt til slutt bør eleven vurdere om svaret som han/hun har kommet frem til er rimelig, ut fra de beregningene som er gjort og ut fra situasjonen som beskrives i teksten.

Ofte observeres det at elever ikke vurderer svar eller at elever aksepterer meningsløse svar (Nortvedt, 2010; Verschaffel et al., 2000). Når elever ser bort fra realistisk informasjon eller begrensninger som det er opplyst om i oppgaveteksten, kan dette ha sammenheng med hva elevene oppfatter som hensikten med skolematematikken (Inoue, 2005; Palm, 2008). Kanskje tenker mange elever at realistiske vurderinger som bygger på egne erfaringer er ugyldige i matematikkundervisningen.

Studien

To studier av sammenhenger mellom leseforståelse og løsing av tekstoppgaver ble gjennomført i 2007 på en slik måte at elever som ligner hverandre, kan identifiseres i de to studiene. Studie 1 var en storskalastudie der resultater fra nasjonale prøver i lesing og regning for et representativt utvalg (N = 1264) ble brukt for å studere sammenhenger mellom lesing og regning for ulike grupper elever. I Studie 2 ble det gjennomført oppgavebaserte intervjuer med totalt 19 elever fra to ulike skoler. Elevene ble bedt om å løse åtte flerstegs tekstoppgaver fra aritmetikkområdet. I tillegg ble resultatene deres fra de nasjonale prøvene samlet inn.

Studie 1

I de nasjonale prøvene er lesing delt inn i tre aspekter: 1) finne informasjon i tekster, 2) tolke og 3) reflektere over innholdet i tekster. I den nasjonale prøven i regning måles elevenes kompetanse innenfor områdene tall, måling og statistikk. For denne studien ble det identifisert tre grupper av oppgaver blant oppgavene som ble gitt innenfor området tall:

• tekstoppgaver som kan løses i ett steg (ettstegsoppgaver)
• tekstoppgaver som kan løses med to eller flere operasjoner (flerstegsoppgaver)
• oppstilte oppgaver som krever en viss regneteknisk beherskelse som for eksempel å kunne utføre subtraksjon med desimaltall (verktøykassa).

For hver elev ble resultatene på leseprøven koblet med resultatene på regneprøven.

Studie 2

Det oppgavebaserte intervjuet ble gjennomført med én og én elev på elevens skole og innenfor elevenes skoletid. Nitten elever med ulik grad av mestring i matematikk, fra å ha store problemer med matematikk til å ligge godt foran jevnaldrende med hensyn til matematisk kompetanse, ble valgt ut ved hjelp av klassenes matematikklærer og ved hjelp av observasjon eller på bakgrunn av resultater fra nasjonale prøver. De åtte oppgavene elevene skulle løse, ble trykket på A4-ark og samlet i et hefte med én oppgave per side. Elevene noterte svar og regnestykker i heftet. Oppgavene var valgt ut slik at alle elevene møtte utfordrende oppgaver der de opplevde å stå fast. Når elevene sto fast, fikk de hint og støtte fra intervjueren. Intervjuer grep ikke inn for å korrigere feil elevene gjorde i oppgaveløsingen.

Intervjuet ble tatt opp på lydbånd, og heftene ble samlet inn. Elevene ble bedt om å tenke høyt når de arbeidet med oppgavene. De valgte selv om de ville løse oppgavene på papir eller ved hoderegning, men de fikk ikke bruke kalkulator. Intervjuene ga innsikt i hvilke vansker elevene møtte både med å forstå og med å løse de åtte tekstoppgavene.

Analyser

Det er i hovedsak gjennomført ulike statistiske analyser med dataene fra Studie 1 som sammenligning av fordeling og gjennomsnitt, i tillegg til å studere korrelasjoner og rangorden. Mer kvalitative studier av svarmønstre ble også foretatt. I Studie 2 ble elevenes forståelse (matematisk modell) av hver oppgave analysert ved å lytte til hvordan eleven løste oppgaven samt ved å studere elevenes notater. Elevenes feil ble analysert for å studere om årsaken til feil var forståelsen av oppgaven, manglende regnetekniske ferdigheter, (manglende) begrepsforståelse, eller manglende tallfakta. Noen feil var også tilfeldige feil som å skrive av feil tall. Dialogene mellom elev og intervjuer ble analysert for å se på turtaking, nivå på støtte, og hva støtten førte til av matematisk aktivitet.

Resultater fra Studie 1 – nasjonale prøver

I figur 1 nedenfor gjengis resultatene på leseprøven og regneprøven for hver elev som deltok i Studie 1.

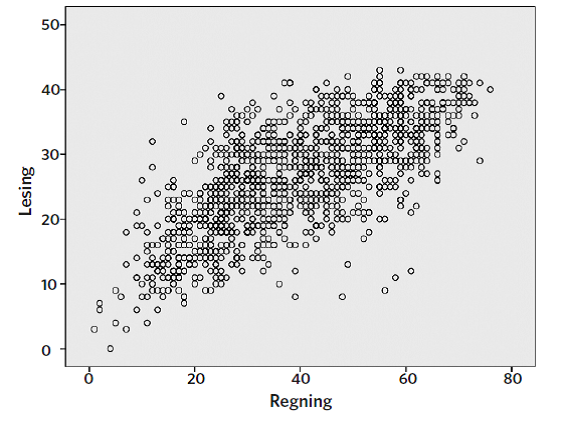
I gjennomsnitt fikk elevene 39,4 poeng av 76 (SD = 15,9), det vil si 52 %, på regneprøven og 26,6 poeng av 42 (SD = 8,2), det vil si 62 %, på leseprøven. Mens guttene skåret signifikant bedre enn jentene på den nasjonale prøven i regning, skåret jentene signifikant bedre enn guttene i lesing, se tabell 1.

Tabell 1. Resultater på nasjonale prøver i lesing og regning for gutter og jenter

Gruppe	Gutter	Jenter
Nasjonal prøve i regning 2007	40,95 (SD=16,7)	37,86 (SD=14,9)
Nasjonal prøve i lesing 2007	25,63 (SD=8,1)	27,6 (SD=82)

Fra figur 1 kan det observeres at det er sterk sammenheng mellom lesing og regning. Tendensen er at dersom eleven var svak i lesing, var eleven også mest sannsynlig svak i regning. Sterke lesere var mest sannsynlig sterke regnere. Dersom man ser hele elevgruppen under ett, kan det observeres at leseforståelse korrelerte høyt med regneferdigheter generelt (r = .859, p = .01) og med flerstegsoppgaver spesielt (r = .631, p = .01). Leseforståelse kan forklare 44 % av variansen i elevenes skåre på flerstegsoppgaver F(1, 1262) = 836,950, p < .001. Tilsvarende funn er gjort i mange internasjonale studier (se for eksempel Roe & Taube, 2006; Vilenius-Tuohimaa, Aunola, & Nurmi, 2008). Det antas at den høye korrelasjonen mellom ferdigheter i lesing og regning skyldes en «usynlig» tredje faktor: en generell evne til problemløsing. Både det å lese ukjent tekst og det å løse en tekstoppgave kan sees på som problemløsing.

Dersom lesing deles opp i de tre leseaspektene finne, tolke og reflektere, korrelerte finne høyest med flerstegs tekstoppgaver. Denne observasjonen kan kanskje forklares med at elevene må finne informasjon i alle tekstoppgaver, men ikke alle oppgaver krever at elevene må tolke og reflektere over innholdet i tekstene. Noen oppgaveformater er typiske eller stereotype, og mange elever vil kjenne dem igjen. Imidlertid viste analysene i Studie 2 at elevene ofte arbeidet med tekstene på et overflatenivå (Nortvedt, 2011b). Det vil si at de da raskt leste gjennom teksten uten å reflektere over sammenhenger i teksten, eller at de leste nøkkelord som signalord. Dette vil vi komme tilbake til.

Noen elever hadde imidlertid et annet mønster enn det som var hovedtendensen. Disse elevene lyktes bedre på den ene prøven enn den andre. Dersom man deler elevene inn i fire grupper ut fra om skåret over eller under middels på hver av de to nasjonale prøvene, fremkommer mønsteret som er gjengitt i tabell 2 nedenfor.

Tabell 2. Fordeling i grupper etter resultater på nasjonale prøver i lesing og regning

Gruppe		Gutter	Jenter	Alle
Under middels regning	%	38,8	39,3	39,1
Under middels lesing	n	245	249	494
Under middels regning	%	6.0	16.7	11.4
Over middels lesing	n	38	106	144
Over middels regning	%	17.1	7.3	12.2
Under middels lesing	n	108	46	154
Over middels regning	%	38.0	36.7	37.3
Over middels lesing	n	240	232	427
	%	100	100	100
	N	631	633	1264

Note: % beregnet for hver kolonne

De fleste elevene (76 %) skåret enten under middels eller over middels på begge prøvene. I begge disse gruppene var det like store andeler jenter og gutter. Den siste firedelen av elevene viste et annet mønster. De skåret over middels på en prøve og under middels på den andre prøven, og her fremkommer et helt annet mønster med hensyn til andelen jenter og gutter i hver gruppe: Signifikant flere gutter skåret over middels i regning og under middels i lesing, mens signifikant flere jenter skåret under middels i lesing og over middels i regning, χ² (df = 3) = 57,237, p < .001.

Gruppen med over middels resultater i regning og under middels resultater i lesing er spesielt interessant. Mange av disse elevene måtte sannsynligvis kompensere for dårlige leseferdigheter når de løste regneprøven. En studie av resultatene deres viste at de gjorde flere feil på grunn av mistolkning av nøkkelord (som vi kommer tilbake til), men samtidig også i større grad enn elever med gode ferdigheter i både lesing og regning, kjente igjen stereotype oppgaver (Nortvedt, 2011a).

Resultater fra Studie 2 – oppgavebaserte intervjuer

Analysen av de oppgavebaserte intervjuene viste at mange av elevene leste oppgavetekstene overflatisk (Nortvedt, 2010). De fokuserte i større grad på at de skulle regne, det vil si løse oppgaven, enn på å forstå hva oppgaven handlet om. Dette er i tråd med annen forskning på problemløsing (se for eksempel Schoenfelds forskning på studenter, 1992). Når elevene leste oppgavene, reduserte de ofte problemet som skulle løses til noe som lå innenfor egen matematisk kompetanse slik som Abraham i eksempelet nedenfor.

Figur 2. Oppgave 8 fra det oppgavebaserte intervjuet.

Tor, Terje og Eva tjente til sammen 31200 kroner på å gå med reklame. Tor skulle ha 3400 kroner mindre enn Terje, og Eva skulle ha 1600 kroner mer enn Terje.
Hvor mye fikk hver av dem utbetalt?

Figur 3. Transkript av Abrahams arbeid med oppgave 8.

Abraham: (leser oppgaven høyt). OK. Tre delt på (uklart, mumler).
En titusen hver (skriver 10 000 kr). Eh. Pluss en firehunder hver (skriver 400 under 10 000).
Så hver fikk 10 400. (pause) kroner.

Oppgave 8 var en krevende oppgave for elever på 8. trinn. Den kan løses på mange ulike måter. De fleste elevene løste oppgaven ved å prøve og feile, men det var også elever som tegnet penger som de «delte ut». Abrahams forenkling av oppgaven resulterte i en matematisk modell som inneholdt et annet problem enn det som står i oppgaveteksten. Tilsvarende forenklinger ble gjort av mange av de 19 elevene på en eller flere oppgaver. De elevene som gjorde slike feil, hadde alle under middels resultater på den nasjonale prøven i regning. Mange strevde også mye med å gjennomføre de nødvendige beregningene fordi de ikke mestret de fire regningsartene. Disse elevene hadde varierende ferdigheter i lesing. Mens noen hadde svært svake resultater i lesing, var andre dyktige lesere.

Ofte var forenklingen et resultat av at nøkkelord som «hver», «til sammen» eller «mer enn» ble brukt som operasjonsord. Disse ordene forteller ofte hvilken operasjon som skal gjennomføres i ettstegsoppgaver der for eksempel ordet «hver» kan fortelle at noe skal fordeles likt på et antall personer. Når nøkkelordene opptrer i flerstegsoppgaver, forteller de snarere om relasjoner mellom mengder og personer. Hvis elevene leser dem som operasjonsord, fører dette til feil i den matematiske modellen, dermed blir resultatet av oppgaveløsingen også feil.

Avsluttende kommentarer

Denne studien viser klare sammenhenger mellom leseforståelse og regneferdigheter samtidig som noen elever viser avvikende mønstre. Det er viktig å arbeide bevisst med lesing i matematikk, særlig med elever med manglende leseferdigheter. For denne gruppen kan det være klokt å arbeide mye med hvordan nøkkelord brukes eller ikke brukes som operasjonsord i matematikktekster. Det kan også være en fordel for disse elevene å bygge seg opp et repertoar av oppgaveformater de kjenner igjen, formater som kan opptre som stereotyper. Mest sannsynlig vil det å arbeide bevisst med disse to aspektene ved å lese og forstå matematikkoppgaver være gunstig for mange flere elever, kanskje alle.

Det å lete bevisst etter nøkkelordene kan være en god strategi dersom eleven reflekterer over om nøkkelordet refererer til en direkte handling, det vil si løsningsmetode, eller om det refererer til relasjoner mellom personer og mengder. Slik bevissthet krever nok mye innsats og trening sammen med klassekamerater og lærer i å lese og tolke teksten i tekstoppgavene. På tilsvarende vis kan man kanskje arbeide med forenkling. Forenkling er en god strategi når oppgaven forenkles til en oppgave med samme matematiske struktur, men som er enklere å løse. Når man som Abraham reduserer oppgaven fra en flerstegstil en ettstegsoppgave, er forenkling en svært uheldig strategi. I og med at elevene da ofte forenkler til noe som ligger innenfor deres egen matematiske kompetanse, kan det være vanskelig for dem å se at det er det de gjør. Igjen vil det være nødvendig å arbeide med analyse av oppgaveteksten i samarbeid med lærer.