Fra å kjenne igjen til å beskrive egenskaper: Om kanter og hjørner

Den følgende samtalen foregår i en 2. klasse tidlig på våren. Elevene ser på og diskuterer definisjoner de har skrevet etter å ha sortert forskjellige mangekanter. «Dette er en 4-kant fordi den har 4 kanter» var en definisjon som flere av elevene hadde kommet fram til (se figur 1). Det viste seg imidlertid at elevene hadde ulik forståelse av hva begrepet kant egentlig innebærer.

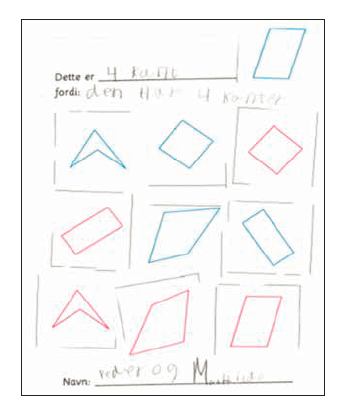
Oda: På mandag jobba dere som matematikere, dere sorterte. Jeg gikk rundt og så på, og det er noe jeg vil høre mer om. Alle gruppene hadde laget seg en haug og sagt at det her er firkanter, for eksempel Rune og Nadia, her er deres ark (fig. 1 kommer opp på smartboarden). De har skrevet «dette er firkant fordi den har fire kanter», og så har de limt på alle figurene som de mener er firkanter. Alle gruppene hadde skrevet det. Kan en av dere fortelle hvordan dere tenkte når dere skrev at den hadde fire kanter. Kan du komme og vise, Rune?

Rune kommer fram og peker på de fire hjørnene mens han teller til fire.

Oda: Ok, så du telte fire. Hva er det som er en kant da, mener dere to?
Peker: Det er de spissene (peker på hjørnene)

Oda: Og du var enig, Nadia? (hun svarer ja)

Oda: Men det var noen grupper som jeg hørte tenke litt annerledes om det med kanter. Kan du, Gustav, fortelle hva du, Kasper og Frida snakket om?

Gustav: Vi tenkte ikke sånn at 1,2,3,4 (peker på hjørnene) men 1,2,3,4 (peker på sidekantene)

Oda: Er det noen som ser forskjellen på det som Nadia og Rune tenkte og det som Gustav, Kasper og Frida tenkte?

Nina: Åja, strekene.

Oda: Hva er forskjellen da, Nina?

Nina: At de telte med strekene og Rune telte med spissene

Oda: Ja, Gustav han sa 1,2,3,4 (peker på sidekantene) mens Rune og Nadia de hadde tenkt sånn, 1,2,3,4 (peker på hjørnene). Hmm.

Oda: Så vi var egentlig litt uenig her om hva en kant egentlig er, noen hadde snakket om kant på én måte (peker på hjørnene) og det var de her, og noen hadde snakket om kant på en annen måte og det var de her (peker på sidekantene). Når matematikerne har sittet slik og snakket sammen så må de bli enige om én ting, de må finne en felles forklaring på hva en firkant er. Så det første jeg tenkte vi må gjøre nå er at vi må finne ut av det her med kant som vi var litt uenige om.

Dagen før samtalen har elevene sortert figurene avbildet i figur 2 i grupper. Oppgaven var å sortere dem ut fra hvilke de mente hørte sammen, og da var det opp til elevene selv å bestemme kriteriene for «å høre sammen». De sorterte først individuelt (én fikk ark med røde figurer, den andre fikk ark med identiske blå figurer) og deretter sammenlignet de med arbeidspartneren.

De fleste parene hadde med gruppene firkanter, femkanter og sekskanter. Ett par hadde skilt ut kvadrat og rektangel som egne grupper, mens ett par hadde ei gruppe kalt tokant (figuren med bue, lengst til høyre i rad 2).

Etter at de hadde blitt enige om navn på figurene i de ulike gruppene, fikk de i oppgave å skrive en definisjon for de forskjellige gruppene og lime på eksempler. Det er resultatet av dette arbeidet figur 1 viser et eksempel på. Vi kommer tilbake til aktivitetene i klasserommet senere i artikkelen.

LaUDiM – et kompetanseprosjekt

Forfatterne av denne artikkelen er deltagere i kompetanseprosjektet LaUDiM (Language Use and Development in the Mathematics Classroom), et fireårig intervensjonsprosjekt som er støttet av Norges forskningsråd gjennom FINNUT-programmet. Kompetanseprosjektet er begrunnet ut fra identifiserte behov i praksisfeltet og skal styrke brukernes medvirkning i praksisrettet kunnskapsutvikling.

Prosjektet er et samarbeid mellom NTNU og to skoler som begge ønsket å utvikle matematikkundervisningen. Episoden som er beskrevet, er hentet fra prosjektets første år.

Kompetanseprosjektet er også et virkemiddel som skal bidra til praksisrettet forskerutdanning og langsiktig kompetanseoppbygging i norske forskningsmiljøer innenfor faglige temaer av stor betydning. Videre er slike prosjekt ment å utvikle kunnskapsgrunnlaget for profesjonsutdanningene, i dette tilfellet lærerutdanningen.

Hovedmålet med LaUDiM-prosjektet er å få større kunnskap om læringsmiljøets betydning for utvikling av de yngste elevenes matematiske tenkning og forståelse, samt deres evne til å framstille matematikk både muntlig og skriftlig. Dette innebærer også evnen til å diskutere matematikk og til å argumentere for og begrunne hvorfor noe er riktig eller eventuelt ikke er riktig.

Et annet mål er å utvikle kunnskap om hvordan lærere kan legge til rette for et miljø som støtter og stimulerer elevenes utvikling av helhetlig matematisk kompetanse og som sikrer at de læringsmålene som settes, blir nådd.

LaUDiM-prosjektet blir utviklet i nært samarbeid mellom forskere ved universitetet og lærere ved de to skolene. Lærere og forskere planlegger og setter mål for undervisningen i fellesskap. En viktig datakilde for forskningen er videoopptak av undervisning og samtaler mellom lærere og elever, og elevene imellom. Elevers skriftlige arbeider er også viktig datamateriale.

Videoopptakene blir diskutert og analysert av forskere og lærere i fellesskap ut fra fastsatte kriterier for målene for undervisningen. Disse diskusjonene blir også filmet og analysert for blant annet å utvikle kunnskap om video som redskap i læreres læring.

Hva er en firkant?

Følgende definisjon vil av de fleste matematikere bli akseptert som definisjon av en firkant:

En firkant er en lukket, plan figur som består av fire punkter (der ikke tre ligger på samme linje) og fire rette linjestykker som forbinder de fire punktene.

Ethvert matematisk begrep har noen egenskaper som et matematisk objekt må ha for at objektet skal falle inn under det gitte begrepet. Dette er egenskaper som er gitt i definisjonen eller som følger som en konsekvens av definisjonen.

For begrepet firkant er slike egenskaper for eksempel at den er en lukket figur med fire hjørner og fire kanter, som utgjøres av rette linjestykker. Videre følger det av dette at summen av de indre vinklene er 360 grader. Slike egenskaper kaller vi kritiske egenskaper. Dette er egenskaper som alle eksempler på et gitt begrep må ha.

Dessuten vil ethvert eksempel på et begrep ha en rekke andre egenskaper som er spesielle for nettopp dette eksemplet. Disse kaller vi ikke-kritiske egenskaper (Hershkowitz, 1990, s. 81). For firkanter kan slike egenskaper for eksempel være at alle vinklene er 90 grader (rektangel) eller at alle sidene er like lange (rombe eller kvadrat).

En litt mer subtil ikke-kritisk egenskap er det at alle vinkler er mindre enn 180 grader. Mange barn vil tenke på dette som en kritisk egenskap, noe som fører til at figuren nederst til høyre i figur 2 av mange ikke regnes som en firkant. Mange vil også i starten tenke på firkant som synonymt med kvadrat.

Å kunne identifisere og snakke om komponenter av en geometrisk figur (f.eks. kanter og hjørner) er en evne som utvikles over tid. Geometriske figurer gjenkjennes først gjennom sin helhetlige form, ikke ut fra sine enkelte komponenter (van Hiele, 1986). Derfor kan man oppleve at små barn vil betrakte figuren nederst til høyre i figur 2 som en trekant fordi selve omrisset av den kan minne om en trekant. Og det er hjørnene som kanskje er mest iøynefallende ved en mangekant, og derfor er det kanskje mest naturlig å telle disse, slik mange av elevene i klassen gjorde.

For at elevene skal få et rikest mulig innhold i begrepet firkant er det viktig at de møter eksempler på firkanter som har stor variasjon av ikkekritiske egenskaper. Dermed kan man kanskje unngå at visse ikke-kritiske egenskaper oppfattes som kritiske.

De fleste lærebøker starter imidlertid med å presentere kun svært spesielle firkanter, med sterke og ensartede ikke-kritiske egenskaper, slik som rektangler og kvadrater. Hvis dette er de eneste eksemplene barna møter i starten, er det stor fare for at begrepet firkant blir for sterkt knyttet til disse spesielle firkantene.

Språklige utfordringer knyttet til dette matematiske innholdet

Siden mangekanter på norsk navngis ved bruk av dagligspråk, en firkant er en figur med fire kanter, og mangekanter med flere kanter følger det samme mønsteret (femkant, sekskant), vil man umiddelbart tro at det ikke er særlige utfordringer knyttet til å lære disse begrepene.

I engelsk er situasjonen en helt annen, da mangekanter fra femkant og oppover navngis ved hjelp av greske ord (pentagon, hexagon, …), som for engelske barn ikke knyttes til noe som hører dagligspråket til. For disse blir det rent memorert kunnskap å vite hva som er en «pentagon» eller en «hexagon ».

Et annet aspekt er at det ikke spiller noen rolle for klassifiseringen om man teller hjørnene eller kantene, det er jo like mange av hver. Derfor kan det være noe tilfeldig om man i et språk fokuserer på kantene eller på hjørnene når man gir navn til mangekanter. På norsk fokuserer man altså på kantene mens man på svensk fokuserer på hjørnene (fyrhörning), og tilsvarende på tysk (Viereck). Og så ser vi altså i vårt eksempel at det ikke er felles forståelse blant barna om hva som er kanter og hva som er hjørner.

Ordet hjørne i seg selv synes å være en språklig utfordring. Dette er et ord fra dagligspråket, man snakker om hushjørne og gatehjørne, og man kan sitte i hjørnet i et rom. Samtidig er det et matematisk begrep, og da representerer det et punkt, punktet der to sidekanter møtes. Så mens det i matematikk er et punkt, altså noe som ikke har utstrekning, er det i dagligspråket et mer romlig begrep, særlig i uttrykket «å sitte i hjørnet».

Men man kan også «stå å henge på gatehjørnet», og da har det også noe romlig over seg, et sted der man kan oppholde seg. På engelsk ville begrepet fra dagligspråket være ‘corner’, mens det matematikkfaglige begrepet er ‘vertex’. Dette er et ord som ikke finnes i dagligspråket. På norsk brukes altså samme ord i dagligspråket som i matematikkspråket.

Ordet kant har i dagligspråket en betydning i retning av et skille mellom noe, en overgang – man kan falle utfor kanten. Eller det er noe som er skarpt – man kan slå seg på bordkanten. Vi har sett at barna for eksempel omtaler hjørnene som ‘spissene’ og kantene som ‘strekene’ når de blir oppfordret til å bruke ord på komponentene i figuren, så ordet ‘kant’ er heller ikke noe som de uoppfordret bruker om disse figurene.

Å lytte til elevene – en forberedelse til helklassesamtalen

Tilbake til klasserommet. Mens elevene jobbet med å sortere figurene i figur 2, gikk Oda rundt og hørte på diskusjonene. På denne måten får hun innsikt i hvilken forståelse elevene har. Hun fanger opp hvordan elever bruker begreper og hvordan de uttrykker seg. Det gir et godt grunnlag for hva hun må fokusere på i helklassesamtalen.

I dette tilfellet ble Oda veldig overrasket over å oppdage at de fleste elevene brukte begrepet kant feil, og at begrepet hjørne omtrent ikke ble brukt. Til tross for at temaet ikke var nytt for dem, var det en stor andel av elevene som ikke brukte begrepene i tråd med allment aksepterte definisjoner.

Dette ville Oda ikke ha oppdaget hvis hun bare hadde sett på de ferdige arbeidene fordi de aller fleste hadde skrevet at «dette er en firkant fordi den har fire kanter», og tilsvarende for de andre mangekantene. Disse definisjonene er, ut fra ordene som brukes, riktige, men skriftbildet viser ikke hva elevene faktisk legger i de ordene de bruker. Oda hadde fanget opp at noen snakket om hjørner, men ingen hadde tatt det med i sine definisjoner. Hun tar det opp i helklassesamtalen:

Oda: Men så hørte jeg noen som brukte et annet ord underveis her, hvilket ord brukte dere, Trine?

Trine: Hjørne.

Oda: Hjørne brukte dere. Hva er det da?

Trine: Vi skrev det ikke, vi skrev kanter, for vi vet ikke egentlig hva hjørner er.

Oda: Ja, jeg hørte noen flere som snakket om hjørner, og det virket som det var flere enn Trine som ikke visste helt hva det betyr.

Gjennom samtalen i klassen kom det fram at elevene brukte flere forskjellige ord om hjørne, både hjørne, kant og spisser ble brukt. Noen skilte mellom de utvendige og de innvendige hjørnene ved å kalle de utvendige for spisser og de innvendige for hjørner. Oda summerer opp: «Hjørne er et viktig ord og kant er et viktig ord. Det vi er uenige om, er hva som er hva».

For å komme nærmere en felles forståelse tar Oda fram et bilde av en ballbinge. Hun ber elevene tenke seg at de står i midten av den og spør hvor de vil gå hvis de skal stille seg inntil kanten. Videre tar hun fram et ark og spør elevene hva de ville gjort om hun bad dem tegne en strek langs kanten av arket. Elevene peker og forklarer, men er fortsatt uenige om hva de forskjellige begrepene betyr.

Til slutt bestemte Oda seg for å fortelle hva matematikerne har bestemt at hjørner og kanter er. Videre skrev klassen en ny felles definisjon av hva en firkant er. Definisjonen hadde med det de hadde oppdaga og blitt enige om:

Dette er en firkant fordi: Den har fire kanter. Den har fire hjørner. Kantene henger sammen.

Sammenligner man denne definisjonen med den matematiske definisjonen av en firkant presentert tidligere, kan man se at den har med de samme elementene, selv om den er uttrykt på «barns vis».

Hva har vi lært?

I prosjektet erfarte vi, da vi begynte å planlegge sammen, at vi veldig raskt begynte å lage konkrete aktiviteter og oppgaver, det elevene skulle jobbe med. Da vi så på videoopptakene fra de første øktene, erfarte vi at vi ikke hadde vært tydelige nok på hva målkunnskapen skulle være. Undervisningen ble ikke tilstrekkelig fokusert, og det gjorde at aktivitetene ikke bidro til at elevene arbeidet med det vi ønsket.

I undervisningen om geometriske figurer, som vi har presentert her, lyktes vi langt bedre med dette. Etter å ha erfart betydningen av å gå grundig inn i det matematiske innholdet, brukte vi ekstra tid på å bestemme målkunnskapen, hva er det viktig at elevene lærer, og hvilke erfaringer trenger de?

I diskusjonen i prosjektgruppa påpekte Oda at utfordringen året før var at elevene trodde at en firkant er enten et kvadrat eller et rektangel. For at elevene skal bli klar over hva en firkant egentlig er, må vi derfor arbeide mye med firkanter som har stor variasjon av ikke-kritiske egenskaper, og i tillegg se både på andre mangekanter og på figurer som ikke er mangekanter.

Vi observerer at lærebøkene i stor grad starter med å presentere spesielle firkanter, særlig kvadrat og rektangel, i motsetning til å legge vekt på egenskapene som gjelder alle firkanter. Dette kan føre til at elevene ikke lærer viktige egenskaper ved en firkant.

Vi observerer også at oppgavene ofte er utformet slik at misforståelsen knyttet til begrepene hjørner og kanter ikke blir oppdaget hvis ikke læreren er bevisst det. For at elevene skal utvikle en god begrepsforståelse er det viktig at læreren avdekker og avklarer innholdet i disse begrepene og eventuelle misforståelser tidlig.

Valg av arbeidsmetode er ikke likegyldig for elevenes læringsutbytte. Både i pararbeidet og i helklassesamtalen må elevene vise, argumentere, resonnere og bli enige. De jobber som matematikere, sier Oda.

Bruk av språk har betydning for læringsutbyttet – språk og begreper læres gjennom bruk av språk (Vygotskij, 1986). Da elevene i 3. klasse jobbet videre med geometri, var det veldig klart for elevene hva som er kanter og hva som er hjørner. I undervisningsøkta vi har presentert, var alle elevene nødt til å engasjere seg i en samtale – det er ikke alltid tilfellet.

Norske studier indikerer at det er lite tid for dialoger mellom lærere og elever eller mellom elevene (Skorpen, 2006), og at kommentarer fra elevene om matematiske ideer sjelden blir tatt opp av læreren (Bjørkås og Bulien, 2010).

Lærere lærer og utvikler seg på mange måter, gjennom kurs, studier, utviklingsarbeid og gjennom å reflektere over egen og andres undervisning. Lærerne i dette prosjektet framhever læringa som ligger i å først analysere det matematiske innholdet i temaet elevene skal arbeide med og deretter tenke nøye gjennom metoder for å få tak i elevenes forforståelse og eventuelle misforståelser.

I prosjektets andre år innførte vi derfor pre-analyse som en egen fase ei uke før vi planla aktiviteter og oppgaver for nye tema. Dette gjorde vi av to grunner. For det første trengte vi mer tid til denne analysen, og for det andre var det behov for tid mellom denne fasen og planlegging av aktiviteter og oppgaver.

Vi mener dette er vel anvendt tid som forberedelse til et nytt tema fordi det gjør undervisningen mer målrettet og aktivitetene i klasserommet mer meningsfylte for alle elever.