Bevisets stilling i matematikkundervisningen
Det matematiske bevis blir gjerne omtalt som kjernen i matematikken. I ny læreplan kan det matematiske beviset først og fremst finnes igjen i kjerneelementet resonnering og argumentasjon. I grunnskolen blir utfordringen å presentere dette temaet på en slik måte at elevene får en alderstilpasset og anvendbar forståelse av matematiske bevis.
Skoleåret 2020/2021 iverksettes ny læreplan, og det er mange endringer knyttet til fagene og deres kompetansemål. En stor endring er innføringen av kjerneelementer. Utdanningsdirektoratet definerer kjerneelementer slik:
Med kjerneelementer mener vi både det viktigste innholdet, og det elevene må lære for å kunne mestre og bruke faget. Det kan altså være kunnskapsområder, metoder, begreper, tenkemåter og uttrykksformer. (Utdanningsdirektoratet, 2019)
Kjerneelementene i læreplan for matematikk definerer hva matematikk i grunnskolen skal være, og hva som inngår i det å ha matematikkompetanse. Vi kan også si at disse kjerneelementene gjenspeiler hva matematikk er i det norske samfunn, og den matematikkompetansen et samfunn trenger fra menneskene som bor der.
Kjerneelementene i matematikk bør også gjenspeile hva matematikere tenker på som matematikk. Reuben Hersch (1997) sier at:
Matematikk må forstås som menneskelig aktivitet, et sosialt fenomen, del av menneskets kultur, utviklet gjennom historien, og begripelig bare i en sosial kontekst. (s.xi, min oversettelse)
Dette synet er på mange måter identifiserbart i kjerneelementenes og kompetansemålenes utforming.
Majoriteten av (eller kanskje alle) matematikere tenker at bevis er det mest essensielle i matematikk, selv om de kan være uenige om hva man kan karakterisere som et matematisk bevis. Det som ikke er eksplisitt uttrykt i ny læreplan, er forestillingen om at matematiske bevis utgjør kjernen i matematikk. Ordet bevis er ikke nevnt i noen kompetansemål for trinn 1–10. Alan H. Schoenfeld (Skott, Skott, Jess & Hansen, 2018) sier at hvis problemløsning er hjertet i matematikk, så er matematiske bevis sjelen til matematikk. Med et slikt standpunkt kan man hevde at om man ikke underviser i matematiske bevis i klasserommet, så er det ikke matematikk som blir undervist i det hele tatt (Skott m.fl., 2018). Men læreplanen er ikke tydelig på bevisets stilling på trinn 1–10, og det kan derfor være relevant å se på hvilke deler av læreplanen som omhandler matematiske bevis, og hvilken rolle bevis bør ha i undervisningen.
Matematiske bevis – en form for argumentasjon
Et av kjerneelementene i læreplanen er Resonnering og argumentasjon:
Resonnering i matematikk handlar om å kunne følgje, vurdere og forstå matematiske tankerekkjer. Det inneber at elevane skal forstå at matematiske reglar og resultat ikkje er tilfeldige, men har klare grunngivingar. Elevane skal utforme eigne resonnement både for å forstå og for å løyse problem. Argumentasjon i matematikk handlar om at elevane grunngir framgangsmåtar, resonnement og løysingar og beviser at dei er gyldige. (Kunnskapsdepartementet, 2018, s. 15)
Siden dette kjerneelementet involverer beviser, kan vi anta at matematiske bevis blir sett på som en type argumentasjon i ny læreplan. Dette er i tråd med det mange i forskningsfeltet også sier. Nadia Douek (1999) sier at «et matematisk bevis kan betraktes som et spesielt tilfelle av argumentasjon » (s. 129, min oversettelse). Stylianides (2007) sier at bevis er matematiske argumenter med visse egenskaper.
Resonnering og argumentasjon har vært tillagt vekt i utvikling av standarder og læreplaner i andre land også. For eksempel er to av åtte standarder i USA sin Common Core State Standards Initiative (2010) å kunne «argumentere abstrakt og kvantitativt» og «konstruere holdbare argumenter og vurdere andres argumentasjon». Det står at elevene skal «forstå og bruke uttalte antakelser, definisjoner og tidligere etablerte resultater i konstruksjon av egne argumenter» (avsnitt 4, min oversettelse). Dette ligner mye på beskrivelser av hva deduktiv argumentasjon er. Og deduktiv argumentasjon er den argumentasjonsformen som danner grunnlaget for matematiske bevis. I finsk læreplan for matematikk på trinn 7–9 står det under Matematisk tänkande och matematiska metoder at «Eleverna funderar på och bestämmer antalet alternativ. De stärker sin förmåga att motivera och dra slutsatser. De övar att tolka och producera matematisk text. Eleverna får insikt i bevisföringens grunder och övar att avgöra sanningsvärdet för påståendesatser» (Utbildningsstyrelsen, 2019, I1).
At resonnering og argumentasjon har en fremtredende plass i ulike standarder og læreplaner, har flere begrunnelser. Én begrunnelse er at utvikling, forståelse av og det å være kritisk til matematiske resonnementer og argumenter er sentrale elementer i matematisk aktivitet og handling (Skott m.fl., 2018). En annen begrunnelse er at man gjennom resonnering og argumentasjon kan utvikle matematisk forståelse innenfor ulike områder av faget, som for eksempel tall, algebra, måling, statistikk og geometri (Skott m.fl., 2018).
I ny læreplan er altså resonnering og argumentasjon et kjerneelement, men i kompetansemålene for trinn 1–10 blir det å argumentere for nesten bare satt i sammenheng med geometri. Betyr dette at hvis matematiske bevis er en form for argumentasjon, så vil matematiske bevis i størst grad være knyttet til geometri i skolematematikken? Det vil i så fall være en videreføring av en tradisjon som man bør ønske seg bort fra, da bevis er kjernen i alle matematiske kunnskapsområder. For å utvide perspektivet bør kjerneelementet Resonnering og argumentasjon derfor tilegnes også andre prosessbeskrivelser i kompetansemålene som å forklare, beskrive og begrunne.
Produkt og prosess
Vi kan betrakte kjerneelementet Resonnering og argumentasjon både som en prosess og et produkt i klasserommet. Som et produkt skal elevene lære de spesifikke egenskapene som matematisk resonnering og argumentasjon har. For eksempel bør undervisningen gjøre elever i stand til å skille mellom ulike typer matematiske argumenter og hva slags type argumentasjon som blir ansett som matematiske bevis. Det å forstå egenskapene til ulike typer resonnering og argumentasjon betyr at elevene får kompetanse i å følge både lærers og medelevers argumentasjon, og de lærer å utvikle egne argumenter (Skott m.fl., 2018). Resonnering og argumentasjon kan også sees på som en prosess for å lære og forstå det matematiske innholdet i faget. Det betyr at resonnering og argumentasjon i klasserommet må være prosesser som skal forklare og skape forståelse, og ikke være noe som bare skal overbevise noen om at et matematiske argument er riktig eller feil. Undervisningen bør altså forklare elevene hvorfor dette argumentet er riktig eller feil. I så tilfelle bør matematisk forklaring vektlegges i klasserommet, og argumentene som brukes som bevis, bør være forklarende. Da er det mer sannsynlig at elevene oppnår høyere forståelse i faget (Skott m.fl., 2018.). Hanna (2018) ser på dette og hva som skal til for at matematikklærere definerer et bevis som forklarende. Bevis er forklarende når de «formidler nyttig innsikt til en gruppe elever på en hensiktsmessig og pedagogisk riktig måte» (s. 3, min oversettelse).
Matematisk bevis i skolematematikken
Stylianides (2007) har definert matematiske bevis på en måte som gjør dem oppnåelige for elever i grunnskolen. Han definerer matematiske bevis som matematiske argumenter som har tre ulike kriterier:
- De bruker utsagn som er akseptert i klasserommet (sett med aksepterte utsagn) som sanne og tilgjengelige uten ytterligere begrunnelse;
- de benytter seg av former for resonnering og argumentasjon som er gyldige og kjente for elevene; og
- de kommuniseres med uttrykksformer (representasjonsformer) som er passende og kjente for elevene. (Stylianides, 2007, s. 291)
Disse kriteriene kan tilby en felles forståelse for hva matematiske bevis kan være i skolematematikken. Kriteriene kommuniserer også at matematiske bevis i skolen bør ha som mål å skulle forklare og skape matematisk forståelse. Disse kriteriene kan brukes gjennom hele skoleløpet, og forhindre at elever kun bruker empirisk argumentasjon til å etablere matematiske antakelser og påstander (Solem, Alseth, Eriksen & Smestad, 2017). En begrunnelse for at Stylianides (2007) definerer kriterier for bevis i skolematematikken, er at matematisk argumentasjon ikke bør være mindre valid bare fordi elevene er unge. Det bør heller være det motsatte, at elevene gjennom hele skoleløpet opplever og erfarer at det er en forbindelse mellom hvilke argumenter vi aksepterer som matematiske bevis. De bør erfare at det vi underviser i skolen, virkelig er matematikkens hjerte og sjel, for å bruke ordene til Alan H. Schoenfeld (Skott m.fl., 2018).
Elevenes bevisforståelse
Elevene kan utvikle ulik bevisforståelse basert på bevisets stilling i undervisningen. Hvis undervisningen er basert på å presentere matematiske bevis kun for å overbevise om at «slik er det», kan elevene utvikle det Harel & Sowder (1998) kaller autoritær bevisforståelse. Hvis en elev har en autoritær bevisforståelse, vil eleven akseptere et matematisk argument som bevis hvis det blir uttalt fra lærer eller står i læreboka. Typiske utsagn en elev kan bruke da er: «Det står i matteboka» eller «Læreren sa at oddetall pluss oddetall gir et partall». Hvis undervisningen lar elevene bruke argumentasjon gjennom naiv empirisme gjennom å bruke observasjoner og generalisere på bakgrunn av dem, kan eleven utvikle empirisk bevisforståelse. Ved en empirisk bevisforståelse baserer elevene argumentene sine på induktiv resonnering med bakgrunn i empiriske undersøkelser (Harel & Sowder, 1998). Et eksempel på dette er at når elever skal avgjøre påstanden oddetall + oddetall = partall, så kan svaret være: «3 + 5 = 8 og 5 + 7 = 12 og 7 + 9 = 16. Ja, det stemmer.»
Et mål i klasserommet bør være å utvikle analytisk bevisforståelse hos elevene. Denne forståelsen viser seg gjennom argumentasjon som tar utgangspunkt i for eksempel generiske eksempler, moteksempler og systematisk undersøkelse av alle tilfeller (Harel & Sowder, 1998; Stylianides, 2007). Et eksempel på argumentasjon gjennom et generisk eksempel kan være: «Hvis du har to oddetall, for eksempel 3 og 7, så kan vi skrive dem som 2 +1 og 6+1, altså som et partall pluss en. Da har vi 2+1+6+1 = 2+6+2, altså tre partall. Når vi legger sammen partall blir summen alltid et partall, så derfor vil summen av 3 + 7 gi et partall, 10». Eleven bruker et enkelt talleksempel og snakker om dette på en generell måte.
Bevisbasert undervisning
Det er stor forskjell på undervisning der elevene skal finne, generalisere og forklare sammenhenger og mønstre i løsningene sine, og det å reprodusere allerede utviklede bevis. For at et matematisk bevis skal oppleves relevant for elevene, bør løsningene deres være et resultat av utforskende aktivitet (Skott m.fl., 2018).
Reid og Vallejo-Vargas (2017) snakker om at man må bruke en verktøykasse (toolbox) i undervisningen. Denne verktøykassen kan relateres til Stylianides (2007), første kriterium for matematiske bevis. Verktøykassen er nyttig fordi læreren må etablere at det er visse teoremer, definisjoner og antakelser som er tatt for gitt i klasserommet. Denne verktøykassen er avhengig av lærerens elevkunnskap og den matematiske kunnskapen elevene har. Det er flere måter å innføre denne verktøykassen på i klasserommet. Spesielt på lavere trinn kan det være fruktbart å synliggjøre innholdet i verktøykassen gjennom den matematiske argumentasjonen som gjøres. Et eksempel som Reid & Knipping (2010) bruker, er at hvis du ønsker at elevene skal finne vinkelsummen i et polygon, så må elevene vite at vinkler kan måles og adderes. Disse antakelsene må plasseres i verktøykassen. Samtidig kan det være elever i klasserommet som dette ikke er åpenbart for, men der dette åpenbares gjennom den argumentasjonen man bruker for å finne vinkelsummen ipolygoner (Reid & Knipping, 2010).
I bevisbasert undervisning vektlegges bruk av matematiske forklaringer som er basert på deduktiv resonnering og argumentasjon. Det er imidlertid viktig å påpeke at det ikke er feil at elevene bruker både induktiv og deduktiv resonnering når de arbeider med matematikk. Faktisk er det slik at de fleste matematikere skifter mellom induktiv og deduktiv resonnering når de utforsker nye matematiske problemer. Forskere har forsøkt å beskrive denne skiftende resonneringen ved å undersøke matematikere når de står overfor et nytt problem og gjør tenkningen sin synlig ved å tenke høyt og skrive, samtidig som de løser problemet (Arzarello, Micheletti, Olivero, & Robutti, 1998; Mariotti, 2006). Man antar at denne skiftende resonneringen er en del av arbeidet med å utvikle matematisk forståelse. Derfor hører ulike typer resonnering og argumentasjon til i klasserommet.
I bevisbasert undervisning kan elevene ha lov til å ha så mange antakelser som de ønsker. Disse antakelsene bør synliggjøres for alle i klasserommet. Dette er en del av den didaktiske kontrakten som etableres i klasserommet. Hvis disse antakelsene skal kvalifisere seg til matematiske sannheter, må de ha sterk støtte fra deduktive argumenter som er evaluert av læreren (Reid & Vallejo-Vargas, 2017). Dette elementet kan relateres til Stylianides (2007) andre kriterium. Det andre kriteriet er viktig fordi vi trenger en spesifikk type argumentasjon for å validere matematikken og kalle noe et matematisk bevis. Å bestrebe og anerkjenne deduktiv resonnering og argumentasjon i klasserommet vil være å nærme seg matematikkens kjerne også på trinn 1–10.
I den didaktiske kontrakten som etableres i klasserommet, bør det ligge forventning om at vi stiller spørsmål ved hvert argument vi fremlegger. Det betyr at det forventes fra elevene at for hver konklusjon de tar, og hvert svar de får, så skal de spørre hvorfor. I denne kontrakten ligger det også forventning om at hvis elevene fremlegger ukorrekte svar, vil disse bli utforsket og diskutert (Reid & Vallejo-Vargas, 2017).
Ulike representasjonsformer
Selv om matematiske bevis i stor grad har blitt knyttet til kjerneelementet resonnering og argumentasjon i denne teksten, vil det være umulig å beskrive bevis som skal forklare og skape forståelse uten sammenheng med andre kjerneelementer. For at et bevis skal være forklarende, må det bestå av representasjonsformer som er kjent for elevene (Stylianides, 2007). Et eksempel på hvordan vi kan uttrykke oddetall + oddetall = partall, er en visuell representasjon som figur 1.
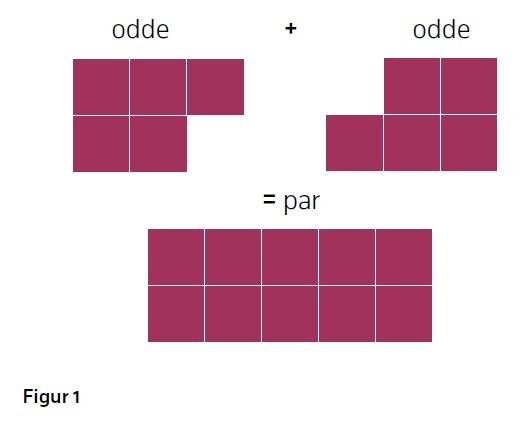
Denne representasjonen kan være mer forklarende enn en algebraisk formell representasjon selv om de begge er basert på deduktiv argumentasjon. Det er viktig å gjøre elevene trygge i å bruke ulike representasjonsformer for å gjøre resonneringen synlig. Dette er også formalisert gjennom et annet kjerneelement: Representasjon og kommunikasjon. Representasjonsformer og kompetanse i å bruke disse i matematikk bør få mer oppmerksomhet. Bruk av deduktiv argumentasjon, og for eksempel visuelle former for bevisgjøring, er avgjørende for at matematiske bevis skal være forklarende og skape relasjonell forståelse i matematikk.
En styrking av bevisets stilling i matematikkundervisningen på trinn 1–10 kan være med på å øke elevenes matematikkompetanse og dermed den matematikkompetanse samfunnet trenger av fremtidens borgere. Den nye læreplanen med sine kjernelementer kan bidra til dette hvis læreren får en forståelse av at matematiske bevis er nært knyttet til kjerneelementet Resonnering og argumentasjon, og til prosessbeskrivelser som: argumentere for, forklare, begrunne og beskrive. Når læreren på trinn 1–10 også har undervisningskompetanse som utvikler elevenes analytiske bevisforståelse, vil undervisningen kunne romme matematikkens hjerte og sjel.
Litteraturhenvisninger
Arzarello, F., Micheletti, C., Olivero, F. & Robutti, O. (1998). A model for analysing the transition to formal proofs in geometry. Innlegg holdt ved the Proceedings of the 22nd Conference of the International Group for the Psychology of Mathematics Education, Stellenbosch, South Africa.
Common Core State Standards Initiative (2010). Mathematics standards. Hentet fra: <http://www.corestandards.org/Math/Practice/>
Hanna, G. (2018). Reflections on proof as explanation. I: A.J. Stylianides & G. Harel (red.), Advances in Mathematics education research on proof and proving. ICME 13 Hamburg: Springer.
Harel, G. & Sowder, L. (1998). Students’ proof schemes: Results from exploratory studies. American Mathematical Society, 7, 234–283.
Hersh, R. (1997). What is mathematics, really? London: Jonathan Cape.
Kunnskapsdepartementet (2018). Kjernelementer i fag. Oslo. Hentet fra: <https://www.regjeringen.no/contentassets/3d659278ae55449f9d8373fff5de4f65/kjerneelementeri-fag-for-utforming-av-lareplaner-for-fag-ilk20-og-lk20s-fastsatt-av-kd.pdf>
Mariotti, M.A. (2006). Proof and proving in mathematics education. I: A. Giutierrez & P. Boero (red.), Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future, 173–204. Rotterdam: Sense.
Nadia, D. (1999). Some remarks about argumentation and mathematical proof and their educational implications. Innlegg holdt ved the European Research in Mathematics Education Osnabrueck.
National Council of Teachers of Mathematics (2014). Principles to actions. Ensuring mathematical success to all. Hentet fra: https://www.nctm.org/uploadedFiles/Standards_and_Positions/PtAExecutive-Summary.pdf>
Reid, D. & Knipping, C. (2010). Proof in mathematics education: research, learning and teaching. Rotterdam: Sense.
Reid, D. & Vallejo-Vargas, E. (2017). Proofbased teaching as a basis for understanding why. Innlegg holdt ved the CERME 10, Dublin, Ireland. Hentet fra: <https://hal.archives-ouvertes.fr/hal-01865651>
Skott, J., Skott, C. K., Jess, K. & Hansen, H.C. (2018). Matematik for lærerstuderende: Delta 2.0 Fagdidaktik, 1.–10. klasse (2. udg.ed.). Frederiksberg: Samfundslitteratur.
Solem, I.H., Alseth, B., Eriksen, E. & Smestad, B. (2017). Tall og tanke: matematikkundervisning på 5. til 7. trinn: 2 (Vol. 2 :). Oslo: Gyldendal akademisk.
Stylianides, A.J. (2007). Proof and Proving in School Mathematics. Journal for Research in Mathematics Education, 38(3), 289–321.
Utbildningsstyrelsen (2019). Grunderna för läroplanen för den grundläggande utbildningen 2014. Kurs 7–9. Hentet fra: <https://eperusteet.opintopolku.fi/#/sv/perusopetus/419550/sisallot/466344?valittu=428782>
Utdanningsdirektoratet (2019). Kjernelementer – fag i grunnskolen og gjennomgående fag i vgo. Hentet fra: <https://www.udir.no/laring-og-trivsel/lareplanverket/fagfornyelsen/kjerneelementer/>