«Det er et verktøy, ikke sant, for oss?» - Erfaringer fra fire gjennomføringer med kartleggingsprøver i regning 2014–2017
I 2014 ble andre generasjon av de statlige kartleggingsprøvene i regning tatt i bruk på 1.–3. trinn i småskolen i Norge. Disse prøvene skal brukes til å identifisere elever som kan ha behov for ekstra oppfølging, og skal i tillegg brukes til vurdering for læring med identifiserte elever. Hva viser kartleggingsprøvene og hvordan jobber lærerne med planlegging og oppfølging av dem?
I 2014 ble andre generasjon av de statlige kartleggingsprøvene i regning tatt i bruk på 1.–3. trinn i småskolen i Norge. Disse prøvene skal brukes til å identifisere elever som kan ha behov for ekstra oppfølging, og skal i tillegg brukes til vurdering for læring med identifiserte elever. Derfor er det mange enkle oppgaver på prøven, slik at lærerne skal få mye informasjon om hva disse elevene mestrer. Kartleggingsprøvene skal normalt ha en levetid på fem år, slik at innholdet i prøvene over tid blir godt kjent for skolene og lærerne. Hva vet vi om norske elevers tallforståelse og regneferdigheter etter fire gjennomføringer, og hvordan bruker lærerne prøvene? Innsamling av elevdata etter hver gjennomføring viser at andelen elever under bekymringsgrensen ikke har sunket i perioden 2014–2017. Elever under bekymringsgrensen viser at de mestrer enkle tellestrategier og at de er i ferd med å utvikle en mental tallinje, men også at de sannsynligvis bruker enkle og kanskje ikke hensiktsmessige regnestrategier. Dybdeintervjuer med sju lærere fra fire skoler viser at de er godt forberedt og påpasselige med å gjennomføre prøvene etter de retningslinjene Utdanningsdirektoratet har fastsatt, men at de strever med å tolke og følge opp resultatene. Enkelte lærere viser også holdninger til prøvene og kartlegging som tilsyne-latende ikke er produktive med tanke på effektiv undervisning. Det antas at målrettet etterutdanning og verktøy som kan hjelpe lærere med å tolke data, vil kunne bidra til en positiv endring der prøveresultater i større grad tas i bruk og at dette på sikt vil føre til at færre elever skårer under bekymringsgrensen.
“This is a tool, isn’t it, for us to use?” Experiences from four implementations of the national mapping tests in numeracy in 2014–2017
In 2014, second generation national mapping tests of numeracy were imple-mented in primary grades 1–3 in Norway. These tests should be used to identify students who might benefit from extra teaching. In addition, test outcomes should be used for assessment for learning. To provide teachers with much information about identified students’ competence, the assessment comprises many easy items. The same mapping tests are normally used for five consecutive years to allow teachers insight into what the tests measure. What do we know about students’ concepts of numbers and calculation strategies after four implementations? How do teachers use insights from the assessments? Analysis of student data collected after each implementation reveals that the number of students identified has not decreased from 2014 to 2017. Students below the cut-off score master simple counting strategies and are in the process of developing a mental number line, but most likely use simple and perhaps unproductive calculation strategies. In-depth interviews with seven teachers from four schools reveal that the teachers are well prepared to implement the assessments, taking care to follow national guidelines developed by the Directorate for Education and Training. However, they struggle to interpret and follow up test outcomes. Some of the teachers reveal beliefs about the assessments and mapping that seemingly are unproductive for effective teaching. Targeted professional devel-opment strategies and tools for teachers to enable them to interpret test data might contribute to developing practices that use test results to a larger extent and in the long term lead to fewer students scoring below the cut-off-score.
Innledning
Likeverdsprinsippet er grunnleggende for norsk skole, og ifølge opplæringsloven skal undervisning innrettes slik at alle elever sikres god opplæring tilpasset deres behov (Lovdata, 2018). Tidligere forskning sammen med nasjonale data fra nasjonale prøver og internasjonale studier gir indikasjoner på at norsk skole kanskje ikke er dyktig nok til å fange opp elever som strever, og at undervisningen sannsynligvis ikke tilpasses den enkelte elev i tilstrekkelig grad. Andelen norske elever som skårer på lavt nivå på nasjonale prøver og internasjonale tester oppfattes som høy (Bergem, Kaarstein & Nilsen, 2016; Grønmo et al., 2012; Utdanningsdirektoratet, 2018). Videre har norske lærere vist en tendens til å vente og se når de opplever at elever strever med å lære seg grunn-leggende ferdigheter (Nordahl & Hausstätter, 2009; van Daal, Solheim, Gabrielsen & Begnum, 2007). Nasjonale data viser også at andel elever som mottar spesialundervisning øker utover i skoleløpet. Dette er ikke et nytt fenomen, men har vært observert i lengre tid (se f.eks. Bonesrønningen, Iversen & Pettersen, 2011; Solli, 2005; Statistisk sentralbyrå, 2011). Norske utdanningsmyndigheter har arbeidet med ulike tiltak for å endre både praksis og holdninger i skolen, og i 2006–2007 ble stortingsmeldingen om tidlig innsats sendt ut (Kunnskapsdepartementet, 2006). I 2008 kom den første kartleggingsprøven i regning rettet mot småtrinnet (Throndsen & Turmo, 2013). Dette tiltaket skulle hjelpe lærere på småtrinnet med å identifisere elever på 2. trinn som kunne trenge ekstra oppfølging. Hensikten med kartleggingsprøver er vanligvis å skaffe informasjon som kan brukes til å tilrettelegge undervisningsaktiviteter for enkeltelever (Ginsburg, 2016). Slike prøver må følges opp av konkrete tiltak for å ha effekt, og det er fordelaktig om kartleggingen er del av mer forpliktende tiltak eller planer (Gersten, Beckmann, Clarke et al., 2009). I Norge brukes samme kartleggingsprøve flere år på rad. Da kan lærere over tid bli godt kjent med innholdet i prøven og kan bruke denne kunnskapen til å tilrettelegge undervisningen. Tanken er at lærerinnsikt gjør det enklere å forebygge svak faglig utvikling. Tilrettelegging vil som regel skje innenfor rammen av fellesskapet, men i enkelte tilfeller kan det være nødvendig med spesialundervisning. Dersom elever ikke klarer å tilegne seg grunnleggende begrepsforståelse – det vil si et godt tallbegrep og strategier for å regne med tall – tidlig i opplæringsløpet, kan dette ha negative konsekvenser for opplæring i matematikkfaget og i andre fag (Scherer, Beswick, DeBois, Healy & Opitz, 2016).
Andre generasjon av de norske kartleggingsprøvene ble tatt i bruk i 2014. Disse prøvene er utviklet for å skille best mellom elever like over og like under en bekymringsgrense (Utdanningsdirektoratet, 2011). Oppgaver og prøver er utviklet ut fra hva nasjonal og internasjonal forskning holder fram som ut-fordringer for lavt presterende elever, knyttet til utvikling av tallbegrep og strategier for å regne med tall. Dersom skoler ikke tilpasser undervisningen på en god måte, kan elevene utvikle det som kalles skoleskapte matematikkvansker. Slike vansker skyldes et misforhold mellom undervisning og elevenes behov og fungering, eller elevers og læreres holdninger til læring og undervisning (Lunde, 2008; Nortvedt, 2017; Scherer et al., 2016).
Hensikten med denne artikkelen er å drøfte erfaringer med fire års gjennomføring av dagens kartleggingsprøver i regning, for å diskutere hvordan prøvene fungerer og om de er et egnet verktøy som kan hjelpe lærere på 1. til 3. trinn med å tilby et likeverdig opplæringstilbud i regning. Elevdata fra fire gjennomføringer og dybdeintervjuer med sju lærere brukes til å drøfte tre problemstillinger:
- Hva viser kartleggingsprøvene at elever med resultater like under bekymringsgrensen mestrer?
- Hvordan arbeider lærere med å forberede, gjennomføre og følge opp kart-leggingsprøvene i regning?
- Hvilke holdninger viser lærere til kartlegging?
Kunnskap om hva elevene like under bekymringsgrensen mestrer, kan gi verdifull innsikt om begreper og ferdigheter som skolene kan nyttiggjøre seg for å iverksette tiltak for å forebygge langsom faglig utvikling. Dermed kan man minske behovet for ekstra hjelp.
Begrepsavklaringer
Termen kartleggingsprøve betegner vanligvis en prøve som brukes til å kartlegge hva elevene kan (Ginsburg, 2016). Ved utforming av kartleggingsprøver i matematikk eller i regning legges det ofte vekt på å kartlegge misoppfatninger (se f.eks. Brekke, 1995; Burkhardt & Schoenfeld, 2018; Ginsburg, 2016). Kartleggingsprøver utformes slik at de kan brukes på hele eller deler av elevgruppen. Prøvene vil med andre ord bestå av oppgaver som er utformet for å måle en større bredde av det konstruktet som måles. Målet med kartleggingsprøvene er vanligvis ikke å skille mellom bestemte grupper av elever, men å kartlegge kunnskaper, ferdigheter, misoppfatninger, strategier osv. hos enkeltelever og i elevgruppen.
I spesialpedagogisk sammenheng brukes ofte screeningtester for å identifi-sere elever som kan ha behov for tiltak (Gersten et al., 2009). En screeningtest er utformet slik at den skal skille sikkert mellom to eller flere grupper av elever. Prøvene utformes slik at det blir mest mulig informasjon om elever like over og like under grensen; man er med andre ord interessert i å utforme prøven slik at det blir så få feilklassifiseringer som mulig.
Termen bekymringsgrense kan på mange måter sammenlignes med en cut-off score. En cut-off score er en grense eller poengsum som bestemmes på screeningtester. Denne poengsummen forteller vanligvis hva som er laveste grense for å ha en viss kompetanse eller ferdighet (Zieky & Perie, 2006).
Kartleggingsprøvene i regning er en hybrid mellom screeningtest og kartleggingsprøve. Prøvene skal skille sikkert mellom elever like over og like under bekymringsgrensen og samtidig gi mye informasjon om identifiserte elever (Utdanningsdirektoratet, 2011). For disse prøvene fungerer bekymringsgrensen som en øvre grense for hvor mange poeng en elev kan ha på prøven og fortsatt bli identifisert som under bekymringsgrensen.
Tidligere forskning
Både i Norge og i andre land strever en del elever med å tilegne seg grunnleggende ferdigheter. Tidligere forskning viser at disse elevene i stor grad bruker rigide og naive strategier ved oppgaveløsing, noe som også er en risikofaktor for senere utvikling av matematikkvansker (Ostad, 2010; Scherer et al., 2016). Elever som bruker slike metoder utvikler svakere begrepsforståelse, og det er en risiko for at elevene utvikler negative holdninger eller vansker med å utføre beregninger og lære matematikk (Geary, 2004; Ostad, 2010; Scherer et al., 2016; Verschaffel, Greer & De Corte, 2007). Når elevene starter på skolen i første klasse, er metoder som fingertelling en vanlig strategi for oppgaveløsing både i praktiske sammenhenger og i matematikktimene. De fleste elever utvikler snart mer fleksible strategier og vil etter hvert beherske skriftlige regnemetoder. Noen elever fortsetter å bruke naive og rigide strategier for fingertelling, såkalte telle-alt-strategier (Ostad, 2001; Ostad & Sørensen, 2007). Disse elevene vil ikke utvikle forståelse for regnemetoder og er spesielt utsatt for langsom progresjon, matematikkvansker eller negative holdninger til matematikk. Selv om metodene elevene bruker er uhensiktsmessige, vil elevene, gitt tilstrekkelig med tid, ofte komme fram til rett svar (Ostad & Sørensen, 2007). Det er derfor utfordrende for lærere å se om elever bruker uhensiktsmessige strategier.
Mestring av regnestrategier er nært forbundet med tallbegrep, og selv om elevene begynner på skolen med «a great deal of informal and intuitive knowledge of mathematics that can serve as a basis for developing understanding of mathematics» (Carpenter, Fennema, Franke, Levi & Empson, 1999, s. 4), er det fortsatt mange elever som opplever utfordringer knyttet til å lære matematikk og grunnleggende ferdigheter i regning på skolen (Verschaffel et al., 2007). Man har lenge visst at ferdigheter med tallregning med små tall (0–9) predikerer ferdigheter i tallregning med flersifrede tall (se f.eks. Carpenter et al., 1999). Videre gir tidligere forskning god innsikt i strategiutvikling innenfor addisjon og subtraksjon, fra telle-alt-strategier via telle-videre-strategier til automatiserte ferdigheter (Geary & Hoard, 2003; Ostad & Askeland, 2008; Ostad & Sørensen, 2007). Samtidig mangler vi kunnskap om hvordan man kan oversette dette til praktiske undervisningsaktiviteter (for en diskusjon se Verschaffel et al., 2007).
Når elevene skal utvikle strategier for å regne med flersifrede tall, utvikler mange misoppfatninger eller rigid strategibruk. Tidligere forskning viser også at elevene bruker standardalgoritmer på svært lite fleksible måter og med liten forståelse (Verschaffel et al., 2007; Wiliam, 2007). Denne utviklingen skyldes blant annet manglende fokus på begrepsforståelse og strategibruk i undervisningen, noe som målrettet undervisning kan motvirke. I rådene som gis av forskere internasjonalt, er det stor optimisme knyttet til hva tidlig innsats kan bidra med når det gjelder utviklingen av grunnleggende regneferdigheter (Gersten et al., 2009; Ginsburg, 2016).
God undervisning handler om flere faktorer, fra holdninger til kunnskap og undervisningsaktiviteter. Ifølge Ginsburg (2016) hører god undervisning sammen med og bygger på god kartlegging, selv om Ginsburg er mest opptatt av vurdering for læring og det daglige arbeidet lærere utfører. Han holder fram at gode verktøy for å kartlegge elevenes kunnskaper og strategier som kan brukes i det daglige arbeidet, er en ønsket løsning for framtiden. I følge Gersten mfl. (2009) finnes det bare moderate bevis for at screening av alle elever fører til bedre resultater. Det trengs noe mer enn bare kartleggingsprøver. Når kartlegging følges opp av intervensjoner som tar tak i de faktiske utfordringene elevene har og med konkrete undervisningsaktiviteter som vektlegger problemløsing i tillegg til begrepsforståelse og strategier, vil kartleggingen ha større effekt og mest sannsynlig gi resultater i form av økt mestring. Mestring er et nøkkelord, og Throndsen og Turmo (2013) fant en positiv relasjon mellom norske læreres vektlegging av mestring og mestringsopplevelse i undervisningen og elevenes resultater på kartleggingsprøvene. Det er viktig at lærere tror at alle elever kan mestre grunnleggende ferdigheter i regning. Tidligere forskning viser at lærere som ikke tror at elevene kan mestre, ofte «holder igjen» faglig og ikke gir elever som strever faglig, like gode muligheter til å mestre mer avanserte begreper og ferdigheter (Scherer et al., 2016). I stedet for å arbeide for gode problemløsingsstrategier og god begrepsforståelse blir kanskje elevene satt til å trene ensidig på enkle rutineferdigheter. I en gjennomgang av forskning på elever med matematikkvansker fant Scherer mfl. (2016) at elever som strever, ofte får mer ensidig undervisning enn andre elever, at aktiviteter er på et lavt kognitivt nivå, og at undervisningen ofte preges av «deficit thinking». Dette står altså i motsetning til rådene om at elever som strever må få utfordringer og gis mulighet til å få arbeide med oppgaver på et, for dem, høyt kognitivt nivå. De må få mulighet til å utvikle gode og robuste begreper og strategirikdom, i tillegg til positive holdninger og mestringsforventninger.
Metode
Denne artikkelen drøfter hva elevresultater fra kartleggingsprøvene i perioden 2014–2017 viser om lavt-presterende elevers grunnleggende ferdigheter i regning. I tillegg drøftes sju læreres holdninger til og erfaringer med å gjennomføre kartlegging og følge opp prøveresultater.
Utvalg av elever
Ved hver gjennomføring trekkes et tilfeldig utvalg av skoler som inviteres til å dele resultatene til én klasse per trinn med forskere på Institutt for lærer-utdanning og skoleforskning (ILS) ved Universitetet i Oslo. Tabell 1 gir en oversikt over størrelsene på utvalgene for perioden 2014–2017.
I 2014 ble 170 skoler trukket ut til deltagelse i følgestudier av kartleggingsprøvene. I de påfølgende årene ble det trukket 60 skoler. Det er frivillig for skolene å delta, og de bes om å delta med én klasse per trinn. Skolene er trukket ut fra Grunnskolens informasjonssystems (GSI) skoleliste. Skoler med færre enn 5 elever på trinnet er ikke tatt med i trekkgrunnlaget. For hver skole er det trukket to reserveskoler. Dersom en skole takket nei til deltagelse, ble første reserveskole kontaktet. Det er ikke skilt mellom primærskoler og reserveskoler i analysene av elevresultater.
Deltagelsen var lavest i 2014, da mellom 70 og 75 % av de utvalgte skolene sendte inn resultater. I de senere gjennomføringene har mellom 80 og 85 % av skolene takket ja til deltagelse og delt elevresultater. Resultatene rapporteres med poeng per oppgave for hver elev. I 2014 rettet mange skoler prøvene sine selv, i 2015–2017 har ILS kodet alle prøveheftene.
Tabell 1. Utvalg av elever i perioden 2014–2017
|
|
2014 |
2015 |
2016 |
2017 |
Totalt |
|
1. trinn |
2280 |
989 |
969 |
906 |
5144 |
|
2. trinn |
2403 |
1102 |
1073 |
890 |
5468 |
|
3. trinn |
2208 |
966 |
983 |
888 |
5045 |
Utvalg av lærere
I 2016 ble det gjennomført semistrukturerte dybdeintervjuer av lærere på fire skoler i to kommuner. Dette er et hensiktsmessig utvalg, basert på at skoler og enkeltlærere har gitt informert samtykke til deltagelse. Sju lærere på til sammen fire skoler samtykte i å bli dybdeintervjuet om hvordan de forbereder seg til og gjennomfører kartleggingsprøvene, samt hvordan de arbeider med å tolke og følge opp prøveresultater. To av lærerne arbeider tett sammen og ble intervjuet i par, de øvrige er intervjuet individuelt. Intervjuene ble gjennomført i et møterom på lærernes skole. Samme intervjuguide ble brukt i alle intervjuene, som ble gjennomført av to personer med tilknytning til prosjektet. Intervjuene varte mellom 45 og 120 minutter.
To lærere på skole A, B og C ble kontaktet via skoleleder. Læreren på skole D ble kontaktet direkte fordi han tidligere hadde henvendt seg til prøvegruppen med mange spørsmål angående kartleggingsprøvene.
Tabell 2. Utvalg av lærere, skole, pseudonym og klassetrinn
|
|
Lærer |
Lærer |
Par/Individuelt |
|
Skole A |
Anna - 2. trinn |
Anita - 1. trinn* |
Individuelt |
|
Skole B |
Bente - 1. trinn |
Brita - 1. trinn |
Par |
|
Skole C |
Carina - 3. trinn |
Camilla - 1. trinn* |
Individuelt |
|
Skole D |
David - 2. trinn |
|
Individuelt |
* Gjennomførte kartleggingsprøver for første gang i 2016
Om kartleggingsprøvene
Kartleggingsprøvene måler grunnleggende ferdigheter i regning i henhold til et nasjonalt rammeverk der regning beskrives som å
bruke matematikk på en rekke livsområder. Å kunne regne innebærer å resonnere og bruke matematiske begreper, fremgangsmåter, fakta og verktøy for å løse problemer og for å beskrive, forklare og forutse hva som skjer. (Utdanningsdirektoratet, udatert a)
Samtidig setter rammeverket for prøvene noen begrensninger: Det skal være minst mulig tekst, slik at elever som strever med å lese kan ta prøvene på like fot med andre elever. Videre avgrenses regning til tallbegrep og regneferdigheter (Utdanningsdirektoratet, 2011). Prøven inneholder oppgaver som måler elevenes kunnskaper om og ferdigheter i telling, forståelse av tallinjen, tallbegrep og ferdigheter i å regne med tall.
Prøvene gjennomføres innenfor en tidsperiode på våren fastsatt av Utdanningsdirektoratet. Skolene er selv ansvarlige for å forberede, gjennomføre og følge opp resultatene i henhold til nasjonale retningslinjer (Utdanningsdirektoratet, udatert b). Resultatene eies av skolen, men skoleeier kan be om innsyn. Kun prøven for 2. trinn er obligatorisk. (Utdanningsdirektoratet, udatert b). De fleste av skolene som er trukket ut i utvalgene har gjennomført prøvene på alle tre trinn selv om prøvene for 1. og 3. trinn er frivillige for skolene.
Prøvene har høy reliabilitet (Chronbachs alfa-verdi mellom 0,92 og 0,94). Bekymringsgrensen ble fastsatt ved første gjennomføring i henhold til ramme-verket utviklet av Utdanningsdirektoratet. Framgangsmåten kan best beskrives som en pragmatisk metode og består i å identifisere den poengsummen som skiller ut de 20 prosentene av elevene som har færrest poeng på prøvene (Utdanningsdirektoratet, udatert b). Denne metoden er mindre sikker enn tradisjonelle og kriteriebaserte standardsettingsmetoder (Zieky & Perie, 2006). Samtidig er alle oppgavene validert med eksterne grupper av eksperter oppnevnt av ILS og av Utdanningsdirektoratet (Nortvedt & Pettersen, 2014).
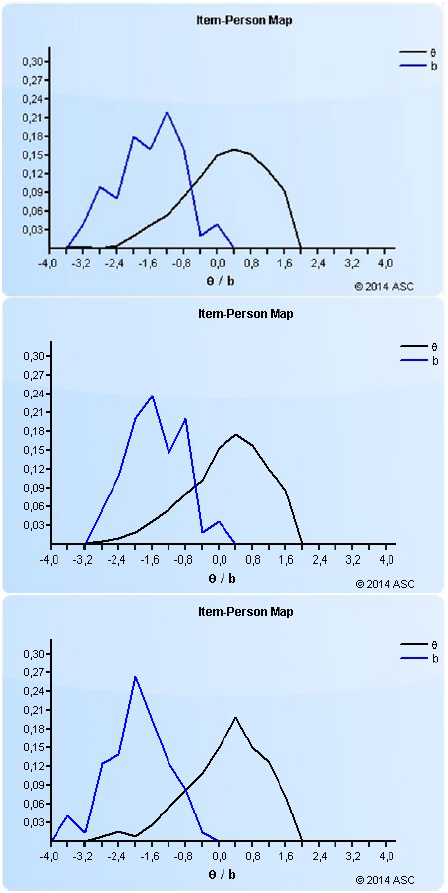
Siden kartleggingsprøvene er en hybrid mellom screening og kartlegging, er det utviklet en god del oppgaver som ligger i nærheten av bekymringsgrensen for å gi mest mulig informasjon i området der bekymringsgrensen skulle settes. Det er også utviklet oppgaver som måler kompetanse på lavere nivåer for å kunne gi informasjon om hva elever under bekymringsgrensen kan. Figur 1 viser relasjonen mellom oppgavene (blå kurve) og elevene (sort kurve) for prøvene for 1., 2. og 3. trinn basert på data fra 2017. Den horisontale aksen viser den felles skalaen som brukes for å angi både oppgavers vanskegrad og elevers dyktighet. En elev med en gitt evne (θ) har femti prosent sannsynlighet for å lykkes med en oppgave med tilsvarende vanskegrad (b). Den vertikale aksen viser frekvens.
Siden prøvene er utviklet for å identifisere elever under en bekymringsgrense, består de av mange enkle oppgaver (Utdanningsdirektoratet, 2011) og har en tilsiktet takeffekt. Mange elever får til alt eller nesten alt på prøven, men samtidig er det ingen oppgaver som kartlegger kompetanse på disse høyere nivåene. Derfor kan prøvene ikke fortelle noe sikkert om hva denne elevgruppen «kan» utover at de kan det kartleggingsprøven måler.
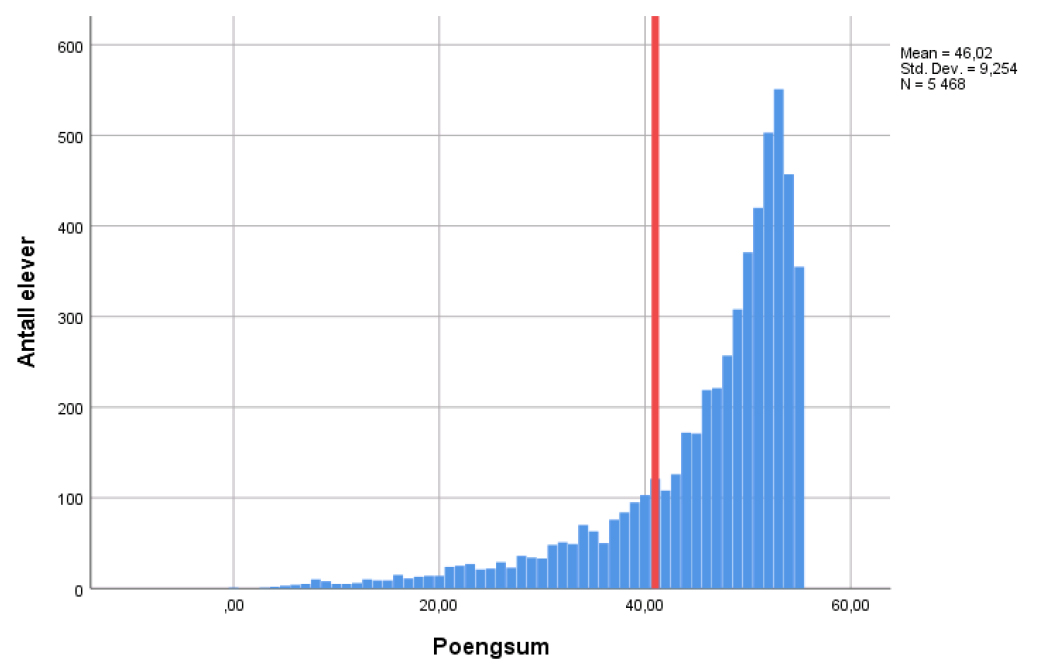
Figur 2 viser de samme fenomenene ut fra elevenes poengsum (råskår) for prøven på 2. trinn for hele perioden 2014–2017. Her er bekymringsgrensen markert med en rød strek. Det kan observeres at en relativt stor andel av elevene som prøven identifiserer i den nedre femdelen av fordelingen, har resultater som ligger like under grensen. Om disse elevene er det mye informasjon fordi de har fått til mellom 67 og 76 % av oppgavene på prøven (37–41 poeng). Disse elevene sies å være «like under bekymringsgrensen». Det er stor spredning i resultatene til elevene som har fått til færrest oppgaver.
Tabell 3 viser hvor stor del av hele utvalget gruppen like under bekymringsgrensen omfatter for de tre prøvene. Tabellen inkluderer også poengsummen som identifiserer bekymringsgrensen.
Tabell 3. Maksimal poengsum og bekymringsgrense for hver prøve, poengintervall for gruppen «elever like under bekymringsgrensen» og andel elever i gruppen
|
Maksimal poengsum |
Bekymrings- grense |
Poengintervall |
Elever like under bekymringsgrensen |
|
|
1. trinn |
50 |
39 |
35-39 |
428 (8,3%) |
|
2. trinn |
55 |
41 |
37-41 |
479 (8,8%) |
|
3. trinn |
72 |
59 |
55-59 |
408 (8,1%) |
Analysemetoder
Det er laget en database per trinn ved at resultater for de fire gjennomføringene er registrert i samme database med elevsvar for hver enkelt oppgave. For å beskrive hva elever like under bekymringsgrensen viser de kan, er det vurdert hvilke oppgaver det er sannsynlig at de vil lykkes med (minst 80 % av elevene i gruppen mestrer) og hva de er i ferd med å mestre (50–80 % av elevene i gruppen mestrer). Data er analysert ved hjelp av deskriptiv statistikk (elev-resultater) samt IRT-metoder (prøvenes fungering).
Dagens kartleggingsprøver skal brukes også i 2019 og 2020; derfor er resultatene ikke rapportert på oppgavenivå, men som beskrivelser av hva elevene typisk mestrer og er i ferd med å lære seg. Beskrivelsene (for alle trinn) legger vekt på telleferdigheter, indikasjoner om indre mental tallinje, tallbegrep og ferdigheter i å regne med tall (addisjon og subtraksjon). Oppgaveeksempler i teksten er fiktive eksempler, men illustrerer sentrale aspekter ved oppgavene som er analysert.
Lærerintervjuene ble transkribert før de ble analysert ved hjelp av meningsfortetting (Yin, 2003; Kvale & Brinkmann, 2009). Det er fokusert på to temaer: 1) planlegge og gjennomføre, og 2) analysere og følge opp. Videre har analysen hatt til hensikt å identifisere hva lærerne ser som hensikten med kartleggingsprøvene, hva de tenker at prøven måler og hvordan de oppfatter elever under bekymringsgrensen. Dette sees som uttrykk for lærernes holdninger til kartlegging. – Bente og Brita er intervjuet sammen og forteller om felles praksis. De er derfor behandlet som en enhet i analysen av lærerintervjuer.
Resultater
I resultatdelen beskrives prøveresultatene for elevene og resultater fra lærer-intervjuene hver for seg. Elevresultatene diskuteres på gruppenivå.
Andel elever under bekymringsgrensen er stabil
Kartleggingsprøvene er utviklet for å fange opp 20 prosent av elevene på hvert trinn. Tabell 4 viser andel elever under bekymringsgrensen ved hver gjennom-føring i perioden 2014–2017. Samme grense brukes i alle gjennomføringer, og fordi prøvens innhold er kjent for skolene, antas det at andelen elever under bekymringsgrensen normalt vil synke over tid. Dels fordi lærere tilpasser undervisningen til prøven og bevisst eller ubevisst trener på prøveinnholdet, dels fordi lærere vil kunne bruke innsikter fra prøvene mer forebyggende etter hvert som de blir bedre kjent med hvilke utfordringer elever har. Det framgår av tabell 4 at vi foreløpig ikke ser tegn til noen slik utvikling. Tvert imot kan det se ut som om andelene med elever under bekymringsgrensen har økt. Her må det tas forbehold om at det kan være systematikk i hvilke skoler som ikke samtykker til å dele data, og at bekymringsgrensen i 2014 kanskje ble satt noe høyt. Resultatene kan imidlertid tas som en indikasjon på at andelen elever under bekymringsgrensen ikke avtar slik som antatt.
Tabell 4. Andel elever under bekymringsgrensen 2014–2017
| 2014 | 2015 | 2016 | 2017 | |
| 1. trinn | 19% | 24% | 24% | 25% |
| 2. trinn | 20% | 25% | 25% | 23% |
| 3. trinn | 19% | 20% | 21% | 22% |
Hva viser kartleggingsprøvene at elever under bekymringsgrensen mestrer?
Elevdata for hvert trinn er analysert for å identifisere hva kartleggingsprøvene viser at elever like under bekymringsgrensen kan.
1. trinn
For prøven på 1. trinn utgjør gruppen like under bekymringsgrensen (35–39 poeng) 428 elever. Analysen viser at disse elevene lykkes med oppgaver som krever at de kan telle med én-til-én korrespondanse og telle oppover i intervallet 1–15, for eksempel 11, 12, 13, også fra et vilkårlig tall. I prøven er det brukt tall i området 0–20, og kanskje kan elevene teller vesentlig lengre og for eksempel over tiere, men dette måles ikke.
Videre viser analysene at elevene kan plassere små tall på rett plass på en strukturert tallinje. Tegninger i enkelte prøvehefter tyder på at noen elever ikke bruker strukturen på tallinjen, men teller fra 0 eller 1 slik som vist i figur 3. Dette elevsvaret viser også hvordan elevene teller med én oppover tallinjen. Slike svar kan tyde på at eleven er i ferd med å utvikle en indre mental tallinje.
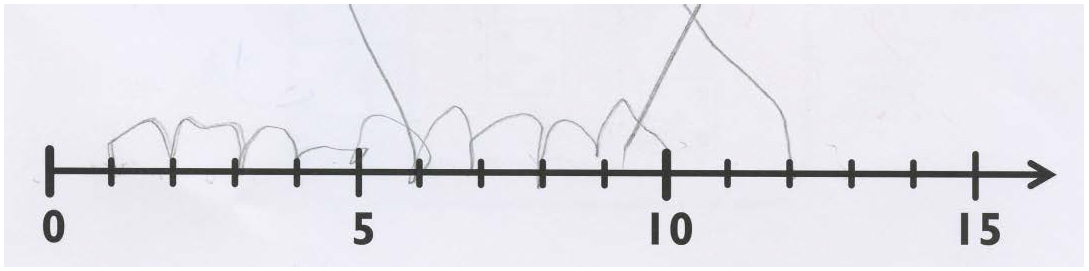
De fleste elevene like under bekymringsgrensen viser at de kan sortere tall mindre enn 12 i riktig rekkefølge. Videre kan de telle opp og sammenligne små mengder, for eksempel gruppert som 5 + 1 + 1 sammenlignet med 1 + 1 + 1 + 1 + 1 + 1. I sum tyder analysene på at elevene er i ferd med å utvikle forståelse av både størrelse på og rekkefølgen av tall. Videre viser analysen at de kan løse oppgaver som inneholder begreper som «nabotall» og «mest». Elevene kan også løse enkle addisjonsoppgaver, både oppstilte oppgaver og oppgaver i kontekst, når summen er mindre enn 10. Dette er små mengder som det er mulig å telle på fingrene, og det er usikkert om elevene løser oppgavene med tellestrategier eller om de kjenner igjen enkle tallfakta. Analysene tyder på at de også er i ferd med å utvide ferdighetene sine til å telle nedover og til å subtrahere to tall når subtrahenden er mindre enn 10. Disse resultatene kan bety at elevene like under bekymringsgrensen er i ferd med å beherske tallområdet mellom 10 og 20.
2. trinn
Mens det i prøven for 1. trinn i stor grad ble brukt tall i områdene 0–10 og 0–20, brukes det tall helt opp til 100 på enkelte oppgaver i prøven for 2. trinn. Samtidig er det også mange oppgaver der elevene bare skal håndtere tall i området 0–20. Valget av tallområde vil føre til at elever som ikke har utviklet forståelse for posisjonssystemet, vil streve med mange av oppgavene i prøven.
Analyser av besvarelsene til de 479 elevene som er like under bekymrings-grensen (37–41 poeng), viser at de sannsynligvis er sikre tellere når de kan telle med én, men at de er i ferd med å lære seg å telle med 2, 5 og 10, for eksempel 20, 22, 24, 26. Svarmønstre viser videre at de kan bruke telleferdighetene sine i oppgaver der de skal telle opp små grupper med konkreter, ofte i form av mynter med valør 20, 10, 5 og 1. Elevene lykkes for eksempel godt med å sammenligne tre grupper med konkreter eller tre tall for å avgjøre hvilken gruppe / hvilket tall som har størst verdi, og de klarer i stor grad å sortere tosifrede tall etter rekkefølge. Mange av elevene like under bekymringsgrensen ble ikke helt ferdige med den siste oppgaven hvor de skal sortere tall etter størrelse, noe som tyder på at de bruker lengre tid på å sammenligne tallene.
Elever som ikke helt mestrer skriftlige konvensjoner eller posisjonssystemet, kan noen ganger skrive tall «baklengs», det vil si bytte om på rekkefølgen av enere og tiere (37 skrives som 73). Selv om elevene på 2. trinn har blitt sikrere på tallinjen og kan bruke kunnskap om rekkefølge på tall, er de sannsynligvis fortsatt i ferd med å lære seg at et tosifret tall er bygget opp av tiere og enere. Forståelse av posisjonssystemet er et sentralt læringsmål på småtrinnet. Svarmønstre tyder på at elevene er i ferd med å forstå at 22 er 2 tiere og 2 enere, og de kan i noen grad bruke denne kunnskapen i oppgaveløsing.
Videre viser analysene at flere elever like under bekymringsgrensen lykkes bedre med å telle opp strukturerte mengder sammenlignet med å dele opp slike mengder. Elevene kjenner kanskje begrepet halvpart, men å fordele en mengde som består av en «stor» mynt og noen enere/kronestykker er utfordrende for elevene. Videre viser analysene at elevene er i ferd med å utvikle strategier for å regne med tall. De fleste i gruppen klarer å addere et ensifret tall til et tosifret, når det ikke innebærer veksling. De klarer også å telle opp små strukturerte mengder, og er i ferd med å lære seg å telle opp større mengder som for eksempel 20 + 10 + 10 + 5 + 1 + 1. Videre viser elevene gjennom sine svar på kontekstualiserte oppgaver at de kan finne opplysninger i illustrasjoner og bruke dem i addisjonsoppgaver. Subtraksjon er fortsatt utfordrende, både oppstilte oppgaver og oppgaver i kontekst. Enkelte elever viser misoppfatninger som sannsynligvis har sammenheng med at de teller for å regne. Et eksempel på dette er når elever tror at rett svar på regnestykker som 14 – 13 er 0; kanskje fordi det ikke er noe tall mellom 14 og 13 når vi teller ned.
3. trinn
Det er til sammen 408 elever som skårer like under bekymringsgrensen (55–59 poeng) på prøven for 3. trinn. Disse elevene har løst omtrent 80 % av oppgavene korrekt. Elevene på 3. trinn er også mest sikre når de skal telle med én, men de viser samtidig at de kan telle oppover med 2, 5 og 10, noe som gir indikasjoner på at elevene behersker strukturen i tallrekka i større grad enn de yngre elevene.
De kan også telle eller summere opp strukturerte grupper, som for eksempel 100 + 100 + 100 + 10 + 10 + 5 + 1. Det er flere indikasjoner på at elevene har etablert en indre mental tallinje og er i ferd med å få et mer utviklet tallbegrep. De kan for eksempel sortere to- og tresifrede tall etter størrelse og til en viss grad bruke strukturene på en tallinje som starter fra 0 (0–50), mens en tallinje som starter fra et vilkårlig tall representerer større utfordringer; det samme gjør tallinjer som har grovere inndeling. Videre viser elevene like under bekymringsgrensen at de kan skrive tall som hundrere, tiere og enere (f.eks. 253 = 200 + 50 + 3).
Analyse av svarmønstre gir indikasjoner på at elevene kan trenge videre støtte og målrettet undervisning som hjelper dem til å utvikle effektive strategier for tallregning. Elevene viser at de kan addere tosifrede tall når operasjonen ikke involverer tierovergang eller veksling. Videre indikerer analysen at elevene er i ferd med å lære seg prinsippene for overganger i addisjonssammenheng, dog ikke i kontekster der de må bruke tallforståelse og strategier for å subtrahere. Det er også tegn som tyder på at elevene har tilegnet seg mer tallfakta (f.eks. addisjons- og multiplikasjonskombinasjoner), og samtidig viser elevene at de bare er i ferd med å ta i bruk slik kunnskap til oppgaveløsing.
Lærernes arbeid med kartleggingsprøvene
De sju lærerintervjuene er analysert for å identifisere hvordan lærerne arbeider med å forberede og gjennomføre kartleggingsprøvene. Hva er enkelt eller mer utfordrende? Hvordan samarbeider de på skolene? Videre fokuseres det på lærernes arbeid med å rette, tolke og følge opp prøvene. Hva opplever de som utfordrende? Tidkrevende? Hvilke strategier har lærerne for å tilrettelegge for elever under bekymringsgrensen og hvilke tiltak iverksetter de? I hele analysen er det også fokus på å identifisere holdninger lærerne viser til kartleggingsprøvene, til elever under bekymringsgrensen og til det å skulle kartlegge.
Forberedelse og gjennomføring
Det varierer fra skole til skole hvordan lærerne mottar informasjon om kartleggingsprøvene. Da intervjuene ble gjennomført i 2016, var det flere av lærerne som fortalte at de mottok informasjon om prøven og gjennomføring fra en av skolelederne ved egen skole. Veiledningen er todelt, der en del av veiledningen ligger åpent tilgjengelig på nettsidene til Utdanningsdirektoratet, mens den delen som inneholder instruks til gjennomføring og informasjon om oppgavene i prøven, krever pålogging. Mens noen lærere fikk begge dokumentene, mottok andre kun instruksen.
De lærerne som hadde tidligere erfaring med gjennomføring av kartleggingsprøver, syntes det var enkelt å sette seg inn i veiledningsmateriellet. Anna fortalte at hun «liker å sitte med [veiledningen] i ro og mak og streke under det som er viktig, sånn i gult, eller ikke sant, eller sånn for meg selv i margen, så det er min forarbeidstid, ja». De to lærerne som gjennomførte for første gang, var derimot overveldet over hvor mye informasjon det var, og strevde med å holde oversikt. Mens Anita gikk til mer erfarne kolleger for hjelp og støtte, hadde Camilla konsentrert seg om å lese instruksen til gjennomføring grundig.
På de fire skolene fortalte lærerne at de samarbeidet med andre lærere på samme trinn om å planlegge gjennomføringen. Skolenes tilrettelegging har karakter av normering og gir indikasjoner om at kartleggingsprøvene har vært i bruk tilstrekkelig lenge til at skolene har utviklet interne (skrevne eller uskrevne) retningslinjer for prøvegjennomføring. Lærerne var opptatt av at elevene skal ha like vilkår under prøven. På skole C gikk 3. trinn lengst i å standardisere; her gjennomførte Carina prøven med de tre klassene på trinnet. I to av klassene fikk hun hjelp av en lærer til å observere elevene mens de arbeidet. De sju lærerne vektla betydningen av å skape like vilkår for alle elever på egen skole. På alle skolene var det lagt til rette for ulike ordninger for å sikre god gjennomføring, som gjennomføring med spesialpedagog eller i liten gruppe. Carina gjennomførte kartleggingen med hele klasser, mens lærerne på skole A, B og D brukte ressurser trinnet hadde, til å dele opp klassene i mindre grupper. Ulike praksiser ble brukt for å dele opp klasser i grupper.
Noen av de lærerne i utvalget som kan karakteriseres som erfarne, gjennomførte kartleggingsprøven effektivt ved å bruke lite undervisningstid til dette. Bente og Brita prioriterte derimot å bruke mye tid. De fortalte at de brukte fire skoledager på å gjennomføre prøven med små grupper under kontrollerte forhold. Da kunne de observere elevene. De la også inn ekstra pauser for å unngå at elevene ble slitne og ukonsentrerte. Anita og Camilla som gjennomførte for første gang, opplevde å streve med det praktiske. Camilla fortalte at situasjonen opplevdes som kaotisk. Hun strevde med å holde på konsentrasjonen til elevene, og opplevde at elevene ikke arbeidet på samme side som henne eller at de ikke fikk med seg instruksjonene hun ga. Hun valgte derfor å gjennomføre prøven på nytt med enkelte elever. Carinas gjennomføring med flere klasser på 3. trinn på samme skole står som en kontrast til dette. Her ble et eget rom på skolen satt av til gjennomføring og selv om hun da gjennomførte med andre elever enn sine egne, opplevde hun at hun mestret å observere elevene under prøvens gang.
Skolene brukte assistenter til prøvegjennomføring på ulike vis, til å holde oppsyn med de elevene som skulle gjennomføre prøven på et annet tidspunkt, til å assistere elever som strevde med å holde konsentrasjon, til å observere bestemte elever eller til å passe tiden under gjennomføringen.
Alle lærerne hadde forberedt elevene sine på prøven. Anita, Brita og Bente fortalte at de også hadde øvd med elevene. Disse tre underviste elever på 1. trinn som skulle ha kartleggingsprøve for første gang. Mens Anita brukte gamle prøver og laget egne oppgaver med samme format som oppgavene i prøven, brukte Brita og Bente eksempeloppgavene på hjemmesiden til Utdannings-direktoratet og trente elevene på å ta imot instruks og arbeide på tid: «og så lagde vi noen andre oppgaver bare for å kjenne på hvor lang tid ett minutt var, hvor mye man rakk å gjøre på ett minutt, bare bli kjente med det… med tiden».
Analysere og følge opp
De sju lærerne sa alle at det var enkelt å rette kartleggingsprøvene, men å tolke og følge opp resultatene var mer utfordrende. Ved prøvetidspunktet (april) kjente de elevene godt, og kunnskap om elevene ble i stor grad brukt når de tolket resultatene, noe dialogen nedenfor mellom Bente og Brita illustrerer:
Bente: tenker at det første, så er det for oss å analysere litt hva som er årsaken til at de har havna der de har havna. For det er noe vi ser at det ...
Brita: Det har vi hatt mange tanker om
Bente: Det er ikke nødvendigvis alltid de er helt reelle de svara, det er jo prøve-situasjonen, har mye å si, konsentrasjonen ...
Lærernes holdninger til prøvene kom til uttrykk når de fortalte om prøveresultatene. Utsagn i intervjuene kan tyde på at de ønsket at alle elever skal få til alt. Selv om de var klar over at prøven var på tid, for å avsløre elever som brukte uhensiktsmessige strategier, kommenterte de fleste av lærerne at elever ikke hadde fått til ting de egentlig kan, eller de hadde fått til mer om de hadde hatt mer tid til å løse oppgavene. Det er også utfordrende for lærerne når elever skåret like under bekymringsgrensen. Utsagn i intervjuene indikerer at lærerne tenkte at det var en spesifikk side i prøven eller type oppgave som var årsaken. Utsagn som «han hadde fått det til med veiledning fra meg», «det er ukjente formater, så derfor må vi øve på formatene på forhånd» eller «de kan det jo egentlig, bare de får nok tid» forteller om holdninger til vurdering og læring som ikke nødvendigvis er produktive. Det var også utfordrende for lærerne at prøven ikke målte kompetansemål i læreplanen. Videre snakket alle om flinke eller sterke elever som får til mye og svake elever som er under bekymringsgrensen. David opplevde dette som et stort dilemma, og følte at han måtte konsentrere seg om å undervise det som måles på kartleggingsprøven. Et fellestrekk for de sju lærerne var at de lette etter feil, de ønsket å identifisere det eleven ikke kunne, som de måtte øve mer på. Dette tyder på at de hadde et tradisjonelt syn på kartlegging, og at det å bruke prøven som grunnlag for vurdering for læring, er et ambisiøst mål. Den eneste av lærerne som snakket om vurdering var Anna, som snakket om hvordan hun bruker partnervurdering i etterarbeidet.
Noen lærere fortalte at de delte resultater og drøftet dem med kolleger. Bente og Brita, som samarbeidet tett, tolket resultatene sammen. De diskuterte hver enkelt side i prøven for hver enkelt elev. Ikke alle var like opptatt av nyansene i prøven, og for dem kunne retting bestå i å (for eksempel Anita). Noen rettet i heftet først, før de registrerte data (Anna) eller «sparte» på resultatene på andre måter, som David som hadde laget seg et regneark. Dette brukte han til å identifisere områder elevene trengte å arbeide mer med.
I følge de sju lærerne foregikk oppfølging i hovedsak innenfor rammene av den daglige undervisningen i klassen. Lærerne brukte organiseringsform, som grupper eller læringspartner eller stasjonsundervisning, til å skape rom for å gi ekstra oppmerksomhet og oppfølging av elever under bekymringsgrensen. De fleste kommenterte ikke hvor mange elever under bekymringsgrensen de hadde, men Anna og Carina, som hadde henholdsvis fire og to elever, fortalte at det er overkommelig å integrere oppfølging i daglig undervisning. I klassen til Camilla var halvparten av elevene under bekymringsgrensen, og det er uklart hvordan hun tenkte å følge opp. David var heller ikke veldig tydelig på hvordan opp-følging av elever under bekymringsgrensen skulle skje, han var mer opptatt av å følge opp områder der klassen som helhet viste svakheter. Selv om Bente og Brita fikk gjort noe oppfølging før sommeren, fortalte de at de i hovedsak «planlegger å følge opp til høsten».
Alle lærerne fortalte at på deres skole hadde de gjennomført foreldresamtaler tidligere på vinteren, og at de derfor allerede hadde snakket med foreldre til elever som strevde med grunnleggende ferdigheter. Det var få som hadde hatt nye foreldresamtaler etter gjennomføringen av prøvene. De fleste hadde sendt noe skriftlig hjem, ringt foreldrene eller snakket med foreldrene i forbindelse med henting av barn på skolen. Ifølge informantene visste de allerede at elevene trengte ekstra oppfølging, og at prøvene først og fremst gir utfyllende informasjon i tillegg til å bekrefte inntrykk de allerede har. Brita sa dette tydeligst, når hun omtalte kartleggingsprøven som et «verktøy for oss», det vil si for lærerne, og mente at resultatene først og fremst skulle brukes internt på skolen.
Diskusjon
Analysen av elevresultatene og lærerintervjuene gir indikasjoner på at det fire år etter innføringen av nye kartleggingsprøver sannsynligvis er utfordrende for skolene å nyttiggjøre seg informasjonen fra prøvene. Resultatene på alle tre trinn viser at elevene like under bekymringsgrensen teller med én og de har noe kjennskap til tallinjen. Elever på 3. trinn kan også telle oppover med 2, 5 og 10. Elever på 3. trinn viser kjennskap til strukturerte tallinjer, og mens elever på 1. trinn kan løse addisjonsoppgaver med sum mindre enn 10, kan elever på 2. og 3. trinn løse addisjonsoppgaver som ikke krever veksling.
For å ha en god faglig utvikling trenger elever å utvikle godt tallbegrep tidlig i skoleløpet (Geary, 2004; Geary & Hoard, 2003; Ostad, 2010). Det er for eksempel helt sentralt å forstå prinsippene som ligger til grunn for posisjons-systemet for å forstå veksling/tierovergang og metoder for å regne med flersifrede tall (Verschaffel et al., 2007). Når elever etter tre års undervisning fortsatt strever med å addere tall som 15 + 7 som krever at de forstår tierovergang, indikerer dette at norsk skole kan bli flinkere til å følge opp de elevene som har lavest prestasjoner på kartleggingsprøvene. På alle trinn gir prøvene innsikt i aspekter ved tallbegrep og regneferdigheter som elevene har tilegnet seg. Samtidig er det kanskje enklere for lærere å legge mest vekt på hva elevene ikke får til. Elever like under bekymringsgrensen trenger å arbeide videre med å tilegne seg strukturen på tallinjen. De trenger også å arbeide mye med tall slik at de kan utvikle bedre forståelse for posisjonssystemet med enere, tiere og hundrere. Videre trenger de å få tid og mulighet til å videreutvikle tellestrategier til strategier for å regne med tall og til å arbeide med enkle problemløsingsoppgaver.
De sju lærerne fortalte at de samarbeidet med kolleger og skapte felles retningslinjer for gjennomføring av kartleggingsprøvene innad på trinnet. Her kan det være viktig å involvere skoleledelsen så det ikke utvikles ulike praksiser eller normer på tvers av trinn på samme skole, slik intervjuene tyder på at det er på skole C.
Lærere må se prøver og vurdering i sammenheng med egen undervisning og kunne omforme prøveresultater til undervisningsaktiviteter. De må også tenke at nettopp dette er hensikten med kartlegging (Ginsburg, 2016). Utfordringene de sju lærerne har, kan ha sammenheng med de holdningene de viser til kartlegging, til elever under bekymringsgrensen og til matematikkundervisning. Ifølge lærerne vet de allerede før prøvene at elevene strever. Utsagn i intervjuene kan tyde på at lærerne finner det vanskelig å bruke informasjonen de får fra prøvene, og alle klarer kanskje ikke å se dem som en del av sin egen vurderingspraksis. Enkelte av lærerne i studien viste misoppfatninger om prøver, at prøver bør utformes slik at alle elevene får til alt. Når elever ikke får til alt, er det fordi lærerne ikke har anledning til å tilrettelegge (nok). Lærere som tenker at elever egentlig kan mer dersom de bare får tilstrekkelig tid, skiller ikke godt nok mellom produktive og rigide strategier. Ifølge Ostad (2010) og Scherer mfl. (2016) er slik kunnskap nødvendig for å kunne støtte god strategiutvikling hos elevene. Lærere som gir uttrykk for at oppgaveformater må være kjent for elevene, indikerer at de tenker på læring som å reprodusere kunnskap. Tidligere forskning viser at det er en risiko for at «svake» elever tilbys tradisjonell undervisning som består i trening og drill (Scherer et al., 2016). Dette forsterkes av fokus på feil snarere enn på hva elevene mestrer, og står i motsetning til hva forskning holder fram som gode strategier for å arbeide med elever som strever (Scherer et al., 2016; Verschaffel et al., 2007). Videre gir intervjuene indikasjoner på at noen av lærerne tenker at enkelte elever ikke kan lære like mye som andre, for eksempel når de bruker uttrykksformer som «svake elever». Dette kan være tegn på det Scherer mfl. (2016) betegner som «deficit thinking».
I følge Gersten mfl. (2009) er effekten av kartlegging avhengig av kvaliteten på tiltak. Intervjuene gir lite informasjon om hvorfor det er vanskelig for lærerne å tolke og følge opp prøvedataene. Lærerne forteller heller ikke om konkrete tiltak de har gjennomført med egne elever. Kanskje viser resultatene at veiledningsmateriellet ikke gir lærerne nok støtte til arbeidet med å følge opp elevene. Det er også mulig at noen av de sju lærerne ikke har lest materiellet på grunn av tidspress, at informasjonsmengden har vært for stor, eller at de ikke visste at de selv kunne laste ned materiellet. Samtidig tyder intervjuene på at lærere som leste alt materiellet, opplevde det som meningsfullt. Lærerne opplevde også god støtte i samarbeid med andre lærere på egen skole, men uerfarne lærere trenger kanskje mer støtte enn «kun» samarbeid.
Ginsburg (2016) mener det er nødvendig med etterutdanning og målrettet skolering for å hjelpe lærerne til å nyttiggjøre seg informasjon fra kartleggings-prøver og andre former for formativ vurdering. Kanskje trengs også verktøy for å «oversette» fra resultater til tiltak. David, for eksempel, hadde forsøkt å lage sitt eget system for å analysere resultater.
Avsluttende kommentarer
Når resultatene brukes på gruppenivå slik som av David, vil de i liten grad legge til rette for differensiering. Dette kan være en hovedutfordring. Tabell 4 viser at andel elever under bekymringsgrensen ikke har sunket som antatt. Disse resultatene tyder på at skolene ikke i tilstrekkelig grad klarer å bruke kartleggingsprøvene til å løfte enkeltelever faglig. Oppgavene i kartleggingsprøvene er laget med utgangspunkt i internasjonal forskning og måler begreper og ferdigheter som elever i begynneropplæringen typisk er i ferd med å lære seg, og som mange strever med. Utfordringer på ett trinn ligner utfordringer på de andre trinnene. Det er få elever som er inkludert i analysene i denne artikkelen, men selv om det knytter seg usikkerhet til prøveresultatene fordi det har vært frafall i utvalget, bekrefter resultatene fra kartleggingsprøvene funn i internasjonal forskning.
Lærere og skoler skal bruke resultatene og planlegge gode tiltak for elever under bekymringsgrensen. Lykkes de ikke, risikerer de at utfordringene til elevene utvikles til skoleskapte vansker. Veldig kort oppsummert trenger mange elever at det legges større vekt på å telle fleksibelt. De må også få arbeide med aktiviteter som hjelper dem å danne et robust tallbegrep. I klasserommet må elevene få utfordringer tilpasset sitt nivå, og de må få arbeide mot flere mål – både bedre begrepsforståelse og bedre strategier. Elever må få muligheter til å gå fra å bruke naive og rigide telle-alt-strategier til mer fleksible strategier for å håndtere tall. Dette er ikke tiltak som er nevnt i lærerintervjuene.
Noen av utfordringene de sju lærerne opplevde, kan ha sammenheng med holdningene de viste til kartlegging og til elever. Det er utfordrende for lærere å endre holdninger, men samtidig viser litteraturgjennomgangen gjort av Scherer mfl. (2016) at produktive lærerholdninger er nøkkelen til god undervisning for elever som strever.
Sju lærere fra fire skoler ble dybdeintervjuet. Resultater fra disse intervjuene kan ikke generaliseres til norske lærere, men intervjuene forteller likevel noe viktig: Det var enkelt for de sju lærerne å sette seg inn i retningslinjene for gjennomføring. For erfarne lærere var det også enkelt å gjennomføre prøvene. Utfordringene lærerne hadde var knyttet til å tolke og vurdere prøvene, til å se hva elevene kunne og til å bestemme hva de skulle legge vekt på i videre undervisning. Kanskje er dette utbredt. Det kan i så fall bidra til å forklare hvorfor andel elever under bekymringsgrensen ikke har sunket i perioden 2014–2017.
Litteraturhenvisninger
Bergem, O. K., Kaarstein, H. & Nilsen, T. (2016). TIMSS 2015: Vi kan lykkes i realfag. Oslo: Universitetsforlaget.
Bonesrønningen, H., Iversen, J. M. V. & Pettersen, I. (2011). Antall enkeltvedtak i grunnskolen øker – til fordel for elever som ikke mottar spesialundervisning. I N. P. Sandbu (red.), Utdanning 2011 – veien til arbeidslivet (s. 101–120). Oslo: NIFU.
Brekke, G. (1995). Introduksjon til diagnostisk undervisning. Oslo: Nasjonalt læremiddelsenter.
Burkhardt, H. & Schoenfeld, A. (2018). Assessment in the service of learning: challenges and opportunities or Plus ça Change, Plus c’est la même Chose. ZDM, 50(4), 571–585. doi: https://doi.org/10.1007/s11858-018-0937-1
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L. & Empson, S. B. (1999). Children's mathematics. Cognitively guided instruction. Portsmouth, NH: NCTM.
Geary, D. C. (2004). Mathematics and learning disabilities. Journal of Learning Disabilities, 37(1), 4–15.
Geary, D. C. & Hoard, M. C. (2003). Learning disabilities in basic mathematics: Difficulties in memory and cognition. I J. M. Royer (red.), Mathematical Cognition (s. 93–116). USA: Information Age Publisher Inc.
Gersten, R., Beckmann, S., Clarke, B. et al. (2009). Assisting Students Struggling with Mathematics: Response to Intervention (RtI) for Elementary and Middle Schools. What Works Clearinghouse: U.S. Department of Education & Institute of Educational Sciences.
Ginsburg, H. P. (2016). Helping early childhood educators to understand and assess young children’s mathematical minds. ZDM, 48(7), 941–946. doi: https://doi.org/10.1007/s11858-016-0807-7
Grønmo, L. S., Onstad, T., Nilsen, T., Hole, A., Aslaksen, H. & Borge, I. C. (2012). Framgang, men langt fram. Norske elevers prestasjoner i matematikk og naturfag i TIMSS 2011. Oslo: Akademika forlag.
Kunnskapsdepartementet (2006). St.meld. nr. 16 (2006–2007). … og ingen sto igjen – Tidlig innsats for livslang læring. Lastet ned 16. juli 2018 fra https://www.regjeringen.no/no/dokumenter/stmeld- nr-16-2006-2007-/id441395/
Kvale, S. & Brinkmann, S. (2009). InterViews: Learning the Craft of Qualitative Research Interviewing. London: Sage
Lovdata (2018). Lov om grunnskolen og den vidaregåande opplæringa (opplæringslova). Lastet ned 16. juli 2018 fra https://lovdata.no/dokument/NL/lov/1998-07-17-61.
Lunde, O. (2008). Matematikkvansker. I A.-L. Rygvold & T. Odgen (red.), Innføring i spesialpedagogikk (s. 94–132). Oslo: Gyldendal Akademisk.
Nordahl, T. & Hausstätter, R. S. (2009). Spesialundervisningens forutsetninger, innsats og resultater. Hamar: Høgskolen i Lillehammer.
Nortvedt, G. A. (2017). Matematikkvansker – en vanske å regne med. I A.-L. Rygvold & T. Ogden (red.), Innføring i spesialpedagogikk (s. 66–88). Oslo: Gyldendal Akademiske.
Nortvedt, G. A. & Pettersen, A. (2014). Første gjennomføring av nye kartleggingsprøver i regning for 1.–3. trinn, 2014. Upublisert rapport. Oslo: EKVA/ILS/UIO.
Ostad, S. A. (2001). Matematikkvansker i et longitudinelt perspektiv. Paper-presentasjon på det 1. nordiske forskerseminaret om matematikkvansker, Kristiansand, Norge.
Ostad, S. A. (2010). Matematikkvansker. En forskningsbasert tilnærming. Oslo: Unipub.
Ostad, S. A. & Askeland, M. (2008). Sound-based number facts training in a private speech internalization perspective: Evidence for effectiveness of an intervention in grade 3. Journal of Research in Childhood Education, 23(1), 109–124.
Ostad, S. A. & Sørensen, P. M. (2007). Private speech and strategy-use patterns: Bidirectional comparisons of children with and without mathematical difficulties in a developmental perspective. Journal of Learning Disabilities, 40(1), 2–14.
Scherer, P., Beswick, K., DeBois, L., Healy, L. & Opitz, E. M. (2016). Assistance of students with mathematical learning difficulties – How can research support practice? – A summary. ZDM, 48(5), 633–649. doi: https://doi.org/10.1007/978-3-319-62597-3_16
Solli, K. A. (2005). Kunnskapsstatus om spesialundervisning i Norge. Oslo: Utdanningsdirektoratet.
Statistisk sentralbyrå (2011). Education statistics. Pupils in primary and lower secondary school. Final figures, 1 October 2011. From http://www.ssb.no/english/subjects/04/02/20/utgrs_en/
Throndsen, I. & Turmo, A. (2013). Primary mathematics teachers’ goal orientations and student achievement. Instructional Science, 41(2), 307–322. doi: https://doi.org/10.1007/s11251-012-9229-2
Utdanningsdirektoratet (udatert a). Rammeverk for grunnleggende ferdigheter. Nettside, lest 16. juli 2018. https://www.udir.no/laring-og-trivsel/lareplanverket/grunnleggende- ferdigheter/rammeverk-for-grunnleggende-ferdigheter/
Utdanningsdirektoratet (udatert b). Kartleggingsprøver. Lastet ned 16. juli 2018 fra https://www.udir.no/eksamen-og-prover/prover/kartlegging-gs/
Utdanningsdirektoratet (2011). Rammeverk for kartleggingsprøver på barnetrinnet. Oslo: Utdanningsdirektoratet.
Utanningsdirektoratet (2018). Utdanningsspeilet. Oslo: Utdanningsdirektoratet.
van Daal, V., Solheim, R. G., Gabrielsen, N. N. & Begnum, A. C. (2007). Norske elevers leseinnsats og leseferdigheter. Resultater fra fjerde og femte trinn i den internasjonale studien PIRLS 2006. Stavanger: Lesesenteret.
Verschaffel, L., Greer, B. & De Corte, E. (2007). Whole number concepts and operations. I F. K. J. Lester (red.), Second handbook of research on mathematics teaching and learning (Vol. 2, s. 557–628). Charlotte, NC: Information Age.
Wiliam, D. (2007). Keeping learning on track. I F. K. J. Lester (red.), Second handbook of research on mathematics teaching and learning (s. 1053–1098). Charlotte, NC: Information Age.
Yin, R. (2003). Case Study Research: Design and Methods. Sage.
Zieky, M. & Perie, M. (2006). A primer on setting cut scores on tests of educational achievement. Educational Testing Service. Hentet fra https://www.ets.org/Media/Research/pdf/Cut_Scores_Primer.pdf