Bevisrelaterte kompetanser i læreplanen LK20 for matematikk i grunnskolen

Innledning

Arbeid med bevis er en sentral del av matematisk arbeid og flere forskere innen matematikkdidaktikk hevder at bevis også må ha en sentral rolle i skolematematikken (se f.eks. Hanna, 1995; Ball, Hoyles, Jahnke & Movshovitz-Hadar, 2002 Stylianides, 2007). I de siste tiårene har flere land tatt inn arbeid med bevis i sine læreplaner og i sine anbefalinger for undervisning i matematikk. Et eksempel er USA der det fremheves at resonnering og bevis skal være en integrert del av all matematikkundervisning:

Reasoning and proof are not special activities reserved for special times or special topics in the curriculum but should be a natural, ongoing part of classroom discussions, no matter what topic is being studied. (NCTM, 2000, s. 342)

Denne trenden gjenspeiles også i den norske læreplanen LK20 i matematikk, som gjelder fra august 2020 (Kunnskapsdepartementet, 2019), der Resonnering og argumentasjon er et av kjerneelementene i matematikkfaget. Kjerneelementer definerer aspekter ved faget som bør gå igjen i arbeid med ulike matematiske temaer, og som elevene må lære for å kunne mestre faget. Argumentasjon i matematikk er beskrevet i kjerneelementet til å handle om at elevene «grunngir framgangsmåtar, resonnement og løysingar og beviser at desse er gyldige» (Kunnskapsdepartementet, 2019, vår utheving). Slik legger også den norske læreplanen opp til at arbeid med resonnering og bevis er integrert i all matematikkundervisning.

Ordene resonnering, argumentasjon og bevis kommer ofte sammen. I denne studien bruker vi begreper hentet fra Jeannotte og Kieran (2017) som er utviklet gjennom en omfattende litteraturstudie. I deres modell er matematisk resonnering et overordnet begrep som omfatter ulike typer prosesser, deriblant å argumentere og å bevise. Både det å argumentere og det å bevise handler om å validere en matematisk påstand, altså finne ut om den er sann eller ikke. En argumentasjon trenger ikke å være matematisk gyldig, den kan for eksempel innebære at man prøver ut påstanden på ulike eksempler og på den måten blir noe mer overbevist om at den er sann. Det å bevise innebærer derimot større grad av deduktiv struktur og stringens enn det å argumentere. Et bevis skal være matematisk gyldig. Man kan si at bevis er argumentasjon som oppfyller noen ekstra krav. Ofte tenker vi på matematiske bevis som formelle og abstrakte, gjerne med algebraiske symboler, og noe vi arbeider med først på ungdomstrinnet og helst enda senere i skolegangen, men det trenger ikke å være slik. Bevis kan være uttrykt på ulike måter og i skolen skal uttrykksmåten tilpasses elevgruppen (Ball & Bass, 2003).

Det er ulike argumenter for hvorfor en skal inkludere arbeid med bevis i skolefaget matematikk. Studier viser at elever tidlig i skolegangen, og også i barnehagen, kan tenke omkring matematiske sammenhenger, og kan argumentere for sine tankeganger når de oppfordres og støttes i slikt arbeid (se f.eks. Ball & Bass, 2003; Cooper & Warren, 2011). Et argument for vektlegging av bevis i skolen er filosofisk: pensum og undervisning i ethvert skolefag bør respektere naturen til det respektive disiplinfaget (Schwab, 1978; Ball & Bass, 2003), være inspirert av det og bruke det på en intellektuell sunn og ærlig måte (Bruner, 1960; Ball, 1993; Lampert, 2001). Et annet argument er pedagogisk: at arbeid med bevis kan støtte meningsskaping og læring i matematikk. At arbeid med resonnering og bevis er nødvendig for dyp læring av matematikk, finner vi eksplisitt uttrykt hos flere forskere (se f.eks. Ball & Bass, 2003; Hanna, 1990). For Hanna og Barbeau (2010) har bevis en rolle som bærere av matematisk kunnskap. Gjennom bevis får elevene kunnskap om nye metoder, verktøy, strategier og begreper som de kan benytte i andre kontekster, spesielt i arbeid med modellering og problemløsing. Stylianides (2016) peker på at arbeid med bevis gir elevene mulighet til å se på arbeid med matematikk som det å skape mening, og slik bli aktive deltakere i egen konstruksjon av kunnskap. Nunokawa (2010) viser til at utforsking, forståelse, forklaringer og bevis henger sammen. Utforsking leder ofte til at elever legger merke til en mulig sammenheng mellom matematiske begreper eller prosedyrer. Slike mulige sammenhenger må da forklares og bevises, noe som igjen fører til økt forståelse for matematiske sammenhenger og begreper. Videre genererer forklaringer og bevis nye begreper og objekter som kan utforskes, så det går en vei fra gode forklaringer og bevis til videre utforsking.

Læreplaner i fag spesifiserer hva som er viktig for elever å lære i skolen, og gjennom det gir de føringer for utforming av læremidler, undervisning og vurdering, og også føringer for læreres profesjonelle utvikling. Tran, Reys, Teuscher, Dingman og Kasmer (2016) hevder at kunnskap om hvordan matematiske temaer blir introdusert og representert, er nødvendig for en fullstendig analyse og forståelse av læreplaner. Gjennom fremheving av Resonnering og argumentasjon som et kjerneelement i matematikk og videre kobling til bevis i definisjon av argumentasjon i LK20, kan man si at læreplanen legger grunnlag for at elever i grunnskolen skal utvikle kompetanser knyttet til arbeid med bevis. En systematisk analyse er likevel nødvendig for å få et bilde av hvordan kompetanser relatert til bevis er ment å utvikles gjennom trinnene. En slik analyse vil kunne bidra i læreres og lærebokforfatteres arbeid med implementering av læreplanen i praksis. Videre vil en systematisk analyse være viktig bakgrunn for senere forskning knyttet til arbeid med bevis i undervisning, læremidler og læringsressurser som tar utgangspunkt i LK20. Forskningsspørsmålet vårt i denne artikkelen er derfor:

Hvordan legger læreplanen LK20 i matematikk opp til utvikling av elevers kompetanser relatert til arbeid med bevis gjennom grunnskolen?

For å identifisere kompetanser som er relatert til bevis i læreplanen, bruker vi et analytisk rammeverk som Hemmi, Lepik og Viholainen (2013) har utviklet for et tilsvarende formål. Rammeverket består av seks ulike kategorier av det de kaller proof-related competences. Kategoriene er utviklet med utgangspunkt i litteraturstudier knyttet til bevis, og i sitt arbeid viser Hemmi et al. (2013) at rammeverket kan brukes til å kategorisere formuleringer i en læreplan og identifisere bevisrelaterte kompetanser som fremheves i læreplanen. Modellen av matematisk resonnering utviklet av Jeannotte og Kieran (2017) omfatter ulike typer prosesser, deriblant å bevise. Vi bruker modellen til å belyse betydningen de ulike bevisrelaterte kompetansene i rammeverket til Hemmi et al. (2013) kan ha for elevers muligheter til å utvikle kompetanse til arbeid med bevis gjennom grunnskolen.

Teoretisk rammeverk

Det er flere rammeverk som er utviklet for å analysere elevers oppfatninger av bevis (f.eks. Balacheff, 1988), arbeid med bevis i skolen (f.eks. Ball & Bass, 2003) eller måten bevis behandles på i lærebøker (f.eks. Stylianides, 2009). Hemmi et al. (2013) har, med utgangspunkt i en litteraturgjennomgang, utviklet en kategorisering av bevisrelaterte kompetanser som kan brukes til å analysere hvordan læreplaner legger opp til kompetanse til å arbeide med bevis, og vi kjenner ikke andre rammeverk som er utviklet til det formålet. Som Hemmi et al. (2013) viser i sin studie, er rammeverket hensiktsmessig for identifisering av viktige aspekter av bevis i læreplaner.

I sitt arbeid tar Hemmi et al. (2013) utgangspunkt i en definisjon av bevis som er utviklet av Stylianides (2007). Han definerer bevis som et matematisk argument, det vil si en kjede av utsagn for eller imot en matematisk påstand, som oppfyller følgende krav:

I. den bruker utsagn som er sanne og fra før kjent og akseptert for en gitt elevgruppe (aksepterte sannheter)

II. den bruker former for resonnering som er matematisk gyldige og kjente / innen rekkevidde for en gitt elevgruppe

III. den er uttrykt ved bruk av hensiktsmessige representasjoner som er kjente / innen rekkevidde for en gitt elevgruppe
(Stylianides, 2007, s. 291–292, vår oversetting)

Eksempler på aksepterte sannheter er definisjoner, aksiomer, matematiske resultater som er bevist tidligere, etablerte prosedyrer og regler. Gyldige former for resonnering innebærer blant annet bruk av logiske slutninger, korrekt bruk av definisjoner eller konstruksjon av et moteksempel for å vise at den gitte påstanden er usann. Argumentet kan være representert ved hjelp av vanlig språk, illustrasjoner, tabeller og symboler (for eksempel algebraisk). Definisjonen til Stylianides (2007) er utformet slik at den tar hensyn både til disiplinfaget og til skolefaget og er slik intellektuelt ærlig. Resonnementet skal være deduktivt og dermed matematisk gyldig. Likevel åpner definisjonen for at beviset er uttrykt på andre måter enn formelle matematiske bevis, og at det bygger på definisjoner og resultater som er kjent i det felleskapet beviset utvikles i.

Den første kategorien i rammeverket til Hemmi et al. (2013), «Proof», viser til formuleringer i læreplaner som eksplisitt nevner bevis, å bevise og deduktiv resonnering. Inkludert her er også formuleringer som peker på elevers arbeid med noen spesielle (typer av) bevis og formuleringer som refererer til elevers metakunnskap om bevis.

Hemmi et al. (2013) peker på at argumentasjon trekkes frem i mange studier som et viktig ledd i utvikling av kompetanse til å arbeide med bevis. Argumentasjon trenger ikke nødvendigvis å være deduktiv og matematisk gyldig, men den har en viktig funksjon ved at den søker etter en forklaring og forståelse. Ifølge Hanna og Barbeau (2010) er forklaring, forståelse og overbevisning blant de viktigste funksjonene av bevis, og de er også relatert til argumentasjon. Derfor kan argumentasjon ses som et viktig utgangspunkt for arbeid med bevis. Kategori to i rammeverket til Hemmi et al. (2013), «Arg», omfatter formuleringer i læreplaner som refererer til argumentering, begrunnelse og validering av egen og andre elevers resonnering og løsninger. Hemmi et al. (2013) argumenter for at også formuleringer som viser til forklaringer, vurdering og evaluering bør være med i denne kategorien da det er begreper som ofte brukes i skolen og innebærer utvikling av matematiske argumenter.

I sin studie viser Hemmi et al. (2013) til undersøkelser (f.eks. Selden & Selden, 1995) som peker på at elever har vansker med å forstå behovet for bevis. Bruk av utforskende aktiviteter som en inngang til bevis har vist seg å være nyttig i så måte (Heinze & Reiss, 2004; de Villiers, 2010). Når elever selv søker etter mønster og sammenhenger og på grunnlag av slike søk fremsetter en hypotese, har de gjerne større behov for å undersøke hvorfor mønsteret/sammenhengen oppstår enn hvis hypotesen er ferdig presentert og de blir bedt om å bevise den. Hemmi et al. (2013) inkluderer derfor kompetansen knyttet til utforsking som en bevisrelatert kategori, «Invest». Den inneholder formuleringer som viser til ulike utforskingsaktiviteter, slike som søk etter regelmessigheter, generalisering, formulering av hypoteser og argumentasjon for at de stemmer.

I arbeid med bevis er det ikke åpenbart hvordan man går frem, og det er viktig å utnytte tidligere kunnskap og sammenhenger mellom ulike begreper og prosedyrer (Maher, 2009). Bruk av ulike representasjoner og veksling mellom dem etter behov fremmes i studier som viktig i alt matematisk arbeid, og også i arbeid med bevis. Kategorien «Struct» til Hemmi et al. (2013) bygger på studier som peker på dette, og inneholder formuleringer i læreplaner knyttet til elevenes utvikling og forståelse av matematiske strukturer og sammenhenger samt bruk av ulike representasjoner.

Hemmi et al. (2013) trekker også frem studier som peker på betydningen av elevers kompetanse til å definere matematiske objekter, forstå betydningen av definisjoner i matematikk og bruke definisjoner i matematisk resonnering og bevis (Heinze & Kwak, 2002; Ball & Bass, 2003; se også Levenson, 2012). Den femte kategorien, «Defn», viser til formuleringer i læreplaner som er knyttet til utvikling av forståelse av definisjoner og deres rolle i matematikk.

Videre peker Hemmi et al. (2013) på at elevers kompetanse til å utvikle logiske tankerekker, formulere kjeder av utsagn på en presis måte og utlede dem fra hverandre, er svært viktig i arbeid med bevis (se også Ball et al., 2002. Den siste kategorien i rammeverket er «Log», og den inneholder formuleringer i læreplaner som viser til de logiske og formelle sidene ved matematikk.

Vi bruker kategoriene til Hemmi et al. (2013) i vår analyse av den norske læreplanen LK20. For å tydeliggjøre betydningen de ulike bevisrelaterte kompetansene kan ha for arbeid med bevis, ser vi bevis i sammenheng med matematisk resonnering, siden bevis er en sentral del av matematisk resonnering. I figur 1 prøver vi å illustrere relasjonene som diskuteres videre i teksten.

Jeannotte og Kieran (2017) har gjennomført en grundig og omfattende gjennomgang av forskingslitteratur om matematisk resonnering (MR), og de har identifisert to ulike aspekt ved MR, et strukturelt aspekt og et prosess-aspekt. Det strukturelle aspektet er et statisk aspekt som er knyttet til ulike former for resonnering i matematikk. De mest kjente formene er deduksjon, induksjon og abduksjon. Det strukturelle aspektet er i liten grad relevant for vår undersøkelse (utover det at det bare er deduksjon som er en gyldig form for resonnering i bevis), og det vil ikke bli omtalt mer her. Ser en på MR gjennom prosess-aspektet, skiller Jeannotte og Kieran (2017) mellom to ulike kategorier av prosesser som er relevante for vår studie – én knyttet til leting etter likheter og ulikheter, og én knyttet til validering. Det er fem prosesser som er relatert til søk etter likheter og ulikheter: identifisering av mønster, sammenligning, generalisering, klassifisering og hypotesesetting. Det er en del forskjeller mellom de ulike prosessene (se mer i Jeannotte & Kieran, 2017), men felles for dem er at de fører til utledning av påstander om matematiske objekter som kan være sanne eller usanne.

 

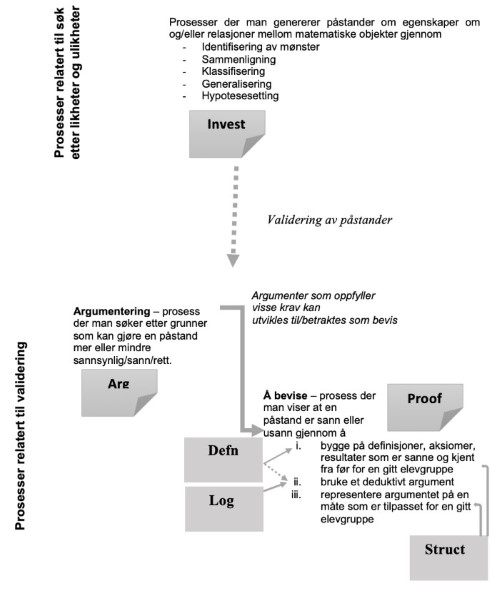
Invest-kategorien til Hemmi et al. (2013) kan sies å sammenfalle i stor grad med prosesser relatert til søk etter likheter og ulikheter, som beskrevet av Jeannotte og Kieran (2017). Gjennom søk etter likheter og ulikheter kommer man frem til en matematisk påstand (for eksempel at «alle tall i 6-gangen er med i 3-gangen» eller at «alle trekanter har en sidekant som er lengst») som kan virke mer eller mindre sannsynlig/sann. Hvis sannheten av påstanden ikke er helt åpenbar for det gitte felleskapet (slik for eksempel «det finnes mange tall som er større enn 5» kan tenkes å være for elever på barnetrinnet), så bør påstanden valideres i videre arbeid.

I rammeverket til Jeannotte og Kieran (2017) omfatter validering prosesser som har som formål å endre sannhetsverdien (epistemisk verdi) til en matematisk påstand, altså finne ut om den er sann eller usann. Det er tre prosesser knyttet til validering: å argumentere (justification), å bevise (proving) og å bevise formelt (formal proving). De tre prosessene er definert med økende grad av deduktiv struktur og stringens. Det innebærer at noen argumenter er bevis, og at noen bevis er formelle bevis. Formelle bevis er kun relevante for disiplinfaget matematikk og ikke relevant for vår studie. Argumentasjon, slik den er definert i MR-rammeverket, innebærer ikke nødvendigvis matematisk gyldighet. For eksempel er «jeg har prøvd mange eksempler fra 6-gangen og alle er også i 3-gangen» et argument som gjør påstanden mer sannsynlig, men ikke nødvendigvis sann siden argumentet er empirisk (se f.eks. Balacheff, 1988 for mer om empirisk argumentasjon). Arg-kategorien til Hemmi et al. (2013) omfatter ulike handlinger som søker å sannsynliggjøre at en påstand er sann, uten at argumentet som utvikles nødvendigvis er matematisk gyldig. Slik sett sammenfaller Arg-kategorien med Jeannotte og Kieran (2017) sin beskrivelse av argumentasjon.

Jeannotte og Kierans (2017) definisjon av bevis drar veksler på Stylianides (2007) sin definisjon. Denne definisjonen brukes også av Hemmi et al. (2013) som utgangspunkt for Proof-kategorien. For at en argumentasjon skal være et bevis, må resonnementet være deduktivt, bygge på definisjoner og resultater som er sanne, og være representert på en hensiktsmessig måte, samtidig som det må være tilpasset en gitt elevgruppe (Stylianides, 2007).

Kunnskap om definisjoner (Defn-kategorien) bidrar direkte til arbeid med bevis. Slik kunnskap inneholder tidligere aksepterte sannheter (punkt (i) i definisjonen av bevis) som kan tas i bruk i utvikling av bevis. For eksempel vil kunnskap om at tall i 6-gangen defineres som multiplumer av 6, altså tall på formen 6n (n et heltall) – eller, mer tilpasset barnetrinnet, tall som kan ordnes i 6 like høye tårn med klosser – gi en måte å starte beviset for påstanden om 3- og 6- gangen. Tydelig bruk av definisjoner vil også bidra til at argumentet som utvikles er logisk oppbygd og deduktivt.

Kunnskap om matematiske sammenhenger og strukturer (Struct-kategorien) bidrar også direkte til arbeid med bevis. Slik kunnskap inneholder tidligere aksepterte sannheter (punkt (i) i definisjon av bevis) som kan tas i bruk i utvikling av bevis. For eksempel kan kunnskap om assosiativ lov for multiplikasjon av hele tall brukes direkte for å bevise at alle tall i 6-gangen også er i 3-gangen (for eksempel ved at siden 6 = 3∙2, så får vi at 6n = (3∙2)n = 3(2n)). Struct-kategorien inneholder også kompetansen til å bruke ulike representasjoner og veksle mellom dem, noe som er viktig for å kunne uttrykke bevis på en hensiktsmessig måte (punkt (iii) i definisjonen). Med utgangspunkt i definisjon av 6-gangen som tall som kan ordnes i 6 like høye tårn med klosser (og tilsvarende for 3-gangen), kan et bevis basere seg på en illustrasjon der to og to tårn slås sammen til tre like høye tårn, som illustrerer et tall i 3-gangen.

For at en argumentasjon skal kunne betraktes som bevis, må resonnementet være deduktivt. Kunnskap om logiske og formelle sider ved matematikk, det Hemmi et al. (2013) samler i Log-kategorien, vil bidra til kompetansen til å utforme deduktive argumenter, som er nødvendig i arbeid med bevis (punkt (ii) i definisjonen).

Vi mener at betydningen av de ulike beviskompetansene identifisert av Hemmi et al. (2013) for arbeid med bevis kommer tydelig frem ved å se bevis som et aspekt av matematisk resonnering slik Jeannotte og Kieran (2017) beskriver det. Relasjonene mellom de ulike kompetansene og deres betydning for elevers utvikling av kompetanse til arbeid med bevis er viktige for vår studie, og vi vil diskutere resultater av vår analyse med utgangspunkt i denne sammenflettingen av bevisrelaterte kompetanser om matematisk resonnering.

Metode

Datamaterialet vårt er læreplan for matematikk som er gjeldende i norsk grunnskole, trinn 1–10, fra 1. august 2020 (Kunnskapsdepartementet, 2019). Læreplanen er organisert i to deler: Om faget og Kompetansemål og vurdering. Den første delen gjelder på tvers av trinn og inneholder en beskrivelse av fagrelevans og sentrale verdier, kjerneelementer i faget som skal fremmes, tverrfaglige temaer som skal tas opp i faget, og ferdigheter som defineres som grunnleggende i faget. I den andre delen, Kompetansemål og vurdering, er det gitt en liste med mål for opplæringen etter hvert trinn (unntatt 1. trinn) og en beskrivelse av hva som skal vektlegges i vurderingen. Som tidligere nevnt, ser vi i denne studien nærmere på den trinnspesifikke delen.

Dataanalysen vår besto av to steg. Først delte vi opp læreplanen i ni enheter: en del som omhandler 1.–2. trinn (gitt i kompetansemål og vurdering 2. trinn), en del som omhandler 3. trinn (gitt i kompetansemål og vurdering 3. trinn), og så videre til 10. trinn. For hver enhet analyserte vi formuleringer, (del)setning for (del)setning, og vurderte om innholdet kunne relateres til innholdet i de seks kategoriene for bevisrelaterte kompetanser i rammeverket til Hemmi et al. (2013). I så fall ble utdraget plassert under den gitte kategorien. Vår analysemetode er det som er kjent som indirekte sammenligningstilnærming (indirect comparison approach) siden vi bruker et predefinert rammeverk i vår koding (Tran et al., 2016). En og samme formulering fra LK20 kunne bli kategorisert i flere kategorier. For eksempel vil en formulering som «utforske og forklare samanhengar mellom brøkar, desimaltal og prosent og bruke det i hovudrekning» inngå i Investkategorien siden det pekes på utforsking, og i Struct-kategorien siden den omhandler sammenhenger.

I vurdering om ulike formuleringer i LK20 er relatert til kategoriene til Hemmi et al. (2013), har vi vært nødt til å gjøre en del valg i noen kategorier. Nedenfor presenterer vi og begrunner valgene:

- Arg: I tillegg til formuleringer som handler om å argumentere, har vi tatt med formuleringer som går på å forklare, begrunne, resonnere og vurdere (slik det er beskrevet i rammeverket) inn i Arg-kategorien. Det var likevel ingen automatikk i kategorisering etter de gitte verbene, og hver formulering ble vurdert utfra innholdet. For eksempel ble ikke «vurdere budsjett» tatt med i Arg-kategorien siden det ikke er snakk om vurdering/begrunnelse av matematisk gyldighet av noe. Også formuleringer som går på å «forklare likningssett» og lignende har vi vurdert å handle om å si hva et begrep går ut på, og ikke argumentasjon. Slike formuleringer er derfor ikke med i Arg-kategorien.

- Invest: Mange formuleringer i LK20 viser til at noe skal utforskes. Begrepet «utforsking i matematikk» er definert under kjerneelementet «Utforsking og problemløysing» som «Utforsking i matematikk handlar om at elevane leiter etter mønster, finn samanhengar og diskuterer seg fram til ei felles forståing». Definisjonen har felles trekk med beskrivelsen av Invest-kategorien, og formuleringene som går på å utforske er blitt tatt med i denne kategorien. Likevel, slik utforsking i matematikk er definert i LK20, er det ikke gitt at mønster og sammenhenger elever kommer frem til, bør valideres. En del formuleringer i LK20 går på at man skal utforske og forklare/argumentere. Slike formuleringer er tatt med i Invest-kategorien, og forklare/argumenteredelen av formuleringen ble tatt med i Arg-kategorien i tillegg. I tillegg til «utforske», er formuleringer som går på å beskrive/kjenne igjen mønster/ sammenhenger/egenskaper og utvikle/beskrive strategier tatt med i denne kategorien, i samsvar med rammeverket til Hemmi et al. (2013).

- Struct: Ifølge rammeverket skal formuleringer som omhandler matematiske sammenhenger og strukturer inngå i denne kategorien. Kategorien handler om kunnskaper elevene kan ta i bruk under arbeid med bevis. I denne kategorien har vi tatt med formuleringer som omhandler matematiske sammenhenger og relasjoner, som mellom begreper, strategier og ulike matematiske tema, i tillegg til formuleringer som går på ulike representasjoner.

- Defn: I en del formuleringer i LK20 står det at man skal forklare et begrep (for eksempel forklare kongruens). Vi har vurdert det slik at det å forklare et begrep kan innebære at man kommer med en (muligens uformell) definisjon, og vi har derfor tatt med slike formuleringer i Defn-kategorien. Bruke matematiske begreper, slik det nevnes i LK20, kan handle om bare å bruke noen ord, men å gjøre det innebærer en viss forståelse for hva ordet/begrepet går ut på. Formuleringen om å teste matematiske begreper fra LK20 kan innebære å undersøke hva en definisjon gjør, hvor dens grenser går. Derfor har vi kategorisert formuleringer som dreier seg om å bruke og teste matematiske begreper som tilhørende i Defn-kategorien.

Noen av kategoriene viste seg å inneholde mange samsvarende utdrag og formuleringer fra de ulike trinnene i læreplanen, og for å få en mer helhetlig oversikt gikk vi et steg videre, nemlig til en oppsummering av resultatene innen hver bevisrelatert kategori for trinn 1–4, trinn 5–6 og trinn 8–10 (den mye brukte inndelingen i norsk grunnskole i barnetrinn, mellomtrinn og ungdomstrinn). De ulike formuleringene ble oppsummert med egne ord, men slik at verbene som ble brukt opprinnelig i LK20 er beholdt. Resultatene er presentert i tabell 1.

Resultater

Tabell 1 viser en oppsummering av formuleringer i LK20 innen hver kategori av bevisrelaterte kompetanser for trinn 1–4, trinn 5–6 og trinn 8–10. Noen av formuleringene i tabellen er generelle grunnet vår oppsummering på tvers av trinn, slik som «Utforske egenskaper av tall og regneoperasjoner» på trinn 1–4 som stammer fra ulike mer spesifikke formuleringer i LK20. Andre ganger er formuleringer generelle fordi de er generelle i LK20, som for eksempel at elevene «testar og bruker matematiske omgrep og forklarer og argumenterer for eigne løysingar». I vår drøfting innen hver kategori kommenterer vi nærmere forholdet mellom generelle og spesifikke formuleringer innen de ulike kategoriene.

Tabell 1. Oppsummering av formuleringer i LK20 (trinn 1–4, 5–7 og 8–10) som hører inn under de ulike kategoriene i rammeverket til Hemmi et al. (2013).

Trinn 1–4
Arg	Forklare og argumentere for egne tenkemåter; argumentere for sortering av geometriske figurer etter egenskaper; begrunne valg av målenheter; forklare sammenhenger mellom regneoperasjoner.
Invest	Utforske egenskaper av tall og regneoperasjoner; utforske og forklare sammenhenger mellom regneoperasjoner; utforske og bruke ulike regnestrategier; utforske og beskrive egenskaper ved geometriske figurer; beskrive mønster i telling, lek og spill.
Struct	Ordne tall, mengder og geometriske former etter egenskaper; representere tall og regneoperasjoner på ulike vis; utforske og forklare sammenhenger mellom regneoperasjoner; beskrive strukturer i lek og spill.
Defn	Teste og ta i bruk matematiske begreper.
Trinn 5–7
Arg	Forklare egne tenkemåter; forklare sammenhenger mellom brøk, desimaltall og prosent; vurdere om løsninger av ligninger og ulikheter er gyldige; begrunne valget av statistisk fremstilling; argumentere for sammenheng mellom radius, diameter og omkrets i sirkler; resonnere over og argumentere for løsninger og matematiske sammenhenger.
Invest	Utforske rasjonale og negative tall og utvikle/utforske regnestrategier med dem; utforske og forklare sammenhenger mellom brøk, desimaltall og prosent; utforske geometriske figurer, areal og omkrets og ulike strategier for beregning av disse; utforske og argumentere for sammenheng mellom radius, diameter og omkrets i sirkler; utforske statistiske data og sentralmål; utforske og reflektere over begreper, representasjoner og strategier i arbeid med ligninger/ulikheter; utforske og reflektere over matematiske sammenhenger.
Struct	Forklare sammenhenger mellom brøk, desimaltall og prosent, og mellom sannsynlighet og brøk; sammenligne regnestrategier for hele og rasjonale tall; representere rasjonale tall og negative tall på ulike vis; utforske, reflektere over og argumentere for matematiske sammenhenger.
Defn	Forklare begrepet ligningsløsning; «beskrive eigenskapar ved og minimumsdefinisjonar av to- og tredimensjonale figurar» og forklare egenskaper til geometriske figurer; kommunisere og argumentere med matematiske begrep.
Log	Løse ligninger/ulikheter gjennom logisk resonnement.
Trinn 8–10
Arg	Argumentere for fremgangsmåter (egne og andres) og resultater, argumentere for ulike sammenhenger i geometri (som f.eks. «mellom sidelengdene i trekantar» og for formler av areal og volum), for statistiske resultater og sammenhenger, for fremgangsmåter og resultater i modellering; forklare struktur og utvikling i geometriske mønster og i tallmønster.
Invest	Utforske matematiske egenskaper og sammenhenger som primtallsfaktorisering, algebraiske regneregler, geometriske sammenhenger, statistiske fremstillinger; beskrive og generalisere mønstre algebraisk; utforske og argumentere for ulike sammenhenger i geometri; utforske og sammenligne egenskaper ved ulike funksjoner; utforske og argumentere for analyser av datasett; utforske matematiske egenskaper og sammenhenger ved å bruke programmering; utforske og generalisere matematiske sammenhenger og strukturer gjennom algebra og andre representasjoner.
Struct	Representere ligninger, ligningssett og funksjoner på ulike vis og se sammenhenger mellom ulike representasjoner; se sammenhenger i funksjoner og algebra; argumentere for sammenhenger i statistikk og mellom statistikk og annen matematikk; utforske og generalisere matematiske sammenhenger og strukturer.
Defn	«Forklare likningar», og forklare «likningssett knytte til praktiske situasjonar», funksjoner, variabel/konstant (i regneuttrykk), begreper som formlikhet og kongruens, og «omgrepa endring per eining og gjennomsnittsfart».

I beskrivelsen av kjerneelementet Resonnering og argumentasjon i den generelle delen av LK20 står det at «Argumentasjon i matematikk handlar om at elevane grunngir framgangsmåtar, resonnement og løysingar og beviser at desse er gyldige». Vi finner ingen formuleringer i kompetansemålene eller underveisvurdering knyttet til enkelttrinn i grunnskolen som viser direkte til bevis eller det å bevise. Det er mulig å tenke at det å bevise er innbakt i begrepet argumentasjon slik det brukes i LK20, noe definisjonen av argumentasjon i LK20 kan peke på. Likevel nevnes altså hverken bevis eller det å bevise eksplisitt i noen formulering i læreplanen som omhandler spesifikke trinn i grunnskolen.

Som tabell 1 viser, finner vi formuleringer som går på argumentasjon og andre prosesser som inngår i argumentasjon, som forklaringer, på alle trinn. For eksempel er det å argumentere for (egne) løsninger en del av underveisvurderingen på alle trinn. En generell formulering om at elevene skal argumentere for matematiske sammenhenger går også igjen i delen som beskriver underveisvurdering på ulike trinn. Vi finner også at kompetansemålene for sjette, åttende, niende og tiende trinn inneholder mål for argumentasjon for konkrete matematiske sammenhenger og/eller fremgangsmåter. For eksempel på 6. trinn er det et mål at elevene skal kunne «måle radius, diameter og omkrins i sirklar og utforske og argumentere for samanhengen» og på 9. trinn at elevene skal «utforske og argumentere for formlar for areal og volum av tredimensjonale figurar». Før 6. trinn nevnes argumentasjon konkret bare på 2. trinn der det står at elevene skal «argumentere for måtar å sortere dei [geometriske figurar] på etter eigenskapar». Derimot finnes det på alle trinn kompetansemål som handler om at eleven skal kunne forklare tenkemåter og sammenhenger. Generelle formuleringer om argumentasjon for løsninger og sammenhenger, i tillegg til formuleringer om konkrete sammenhenger som skal forklares eller argumenteres for, kan gi mulighet til arbeid med argumentasjon gjennom hele grunnskolen.

Det er mange formuleringer i LK20 som går på at elevene skal utforske. Et ordtellingsprogram viser at «utforske» er det ordet i læreplanen med størst frekvens (58 ganger). Utforsking og problemløysing er definert som et kjerneelement i LK20, og det gjenspeiles i mange kompetansemål på alle trinn som går på at elever skal utforske konkrete matematiske sammenhenger og egenskaper til matematiske objekter. Utforsking er definert i den generelle delen av LK20 som «Utforsking i matematikk handlar om at elevane leiter etter mønster, finn samanhengar og diskuterer seg fram til ei felles forståing». Det er ikke klart utfra definisjonen om utforsking innebærer at man bør finne ut hvorfor mønstrene/ sammenhengene er slik de er, altså validere dem. Noen ganger kommer verbet «utforske» alene i LK20, som i «utforske multiplikasjon ved teljing», andre ganger sammen med et annet verb, ofte «utforske og beskrive» eller «utforske og bruke». Formuleringene som går på at noe skal utforskes og forklares / argumenteres for brukes også (i 11 tilfeller av de 58 der utforske brukes). I slike tilfeller er det dermed presisert at mønster og sammenhenger man finner skal valideres. Likevel er det som oftest ikke sagt tydelig om sammenhenger skal valideres. Da er det opp til læreren å bestemme om utforsking stopper ved at man har kommet frem til en påstand om hvordan en sammenheng kan være, eller om man skal fortsette med å finne ut om påstanden stemmer / ikke stemmer og hvorfor.

Vi finner formuleringer på alle trinn som går på sammenhenger og relasjoner mellom ulike begreper og/eller områder i matematikk, og som da inngår i Struct-kategorien. Eksempler er formuleringer som går på «samanhengar mellom addisjon og subtraksjon» og «samanhengar i og mellom statistikk og annan matematikk». Bruk av ulike representasjoner og veksling mellom dem er definert som en del av et kjerneelement i matematikk, og formuleringene knyttet til det går igjen i læreplanen og er med i Struct-kategorien. Ordet (matematisk) «struktur» er derimot lite brukt og ikke definert i LK20. Som oftest brukes det i forbindelse med figur- og tallmønster, eller i generelle formuleringer som «matematiske samanhengar og strukturar». Vår analyse peker på at LK20 legger opp til at det skal arbeides med ulike sammenhenger, relasjoner og representasjoner i matematikk, noe som er viktig for elevers utvikling av bevisrelatert kompetanse.

Vi finner kun én formulering i LK20 som eksplisitt viser til det å utarbeide eller ta i bruk definisjoner: etter 6. trinn skal elevene kunne «beskrive eigenskapar ved og minimumsdefinisjonar av to- og tredimensjonale figurar». Det finnes generelle formuleringer som går på å bruke/teste matematiske begreper i delen om underveisvurdering for ulike trinn. Videre er det kompetansemål på flere trinn som sier at elevene skal kunne forklare et gitt begrep. Dette er kompetansemål som kan innebære at elever blir kjent med konkrete definisjoner i undervisningen, og at de får kjennskap til betydning og bruk av definisjoner i arbeid med matematikk. Samtidig, siden definisjonsbegrepet ikke er gjort eksplisitt, er det opp til lærebokforfattere og lærere i hvilken grad det å bruke/teste/forklare begreper vil bli knyttet til arbeid med definisjoner.

Det er bare én formulering i LK20 der ordet logikk/logisk brukes: i et av kompetansemålene etter 5. trinn står det at elevene skal «løyse likningar og ulik- skapar gjennom logiske resonnement». Vi finner heller ikke noen formuleringer som kan tenkes relatert til Log-kategorien i rammeverket til Hemmi et al. (2013) uten at ordene logikk eller logisk er brukt eksplisitt.

Diskusjon

I denne studien har vi analysert den nye læreplanen i matematikk i Norge for å finne ut hvordan læreplanen LK20 i matematikk legger opp til utvikling av elevers kompetanser relatert til arbeid med bevis gjennom grunnskolen. Med utgangspunkt i vår analyse av læreplanen, vil vi nå drøfte muligheter for utvikling av elevers kompetanser relatert til arbeid med bevis. Her trekker vi frem betydningen de ulike bevisrelaterte kompetansene kan ha for arbeid med bevis. Dette har vi tydeliggjort i figur 1 der vi setter bevis i sammenheng med matematisk resonnering.

Som tidligere diskutert kan man betrakte matematisk resonnering som bestående av to typer prosesser (Jeannotte & Kieran, 2017): prosesser som går på søk etter likheter og ulikheter og som resulterer i formulering av en påstand om matematiske objekter, og prosesser knyttet til validering av matematiske påstander som handler om å finne ut om den gitte påstanden er sann eller usann. Den nye læreplanen har en klar forventning om at elevene skal arbeide med matematisk resonnering. LK20 inneholder formuleringer på alle trinn som omhandler prosesser knyttet til søk etter likheter og ulikheter. Det betyr at læreplanen gir muligheter til å arbeid med dette aspektet ved matematisk resonnering: gjennom identifisering av mønster, generalisering, sammenligning og lignende prosesser skal elever fremsette matematiske påstander. Slike påstander som ikke er åpenbare for det gitte fellesskapet bør i matematikk videre valideres gjennom argumentasjon eller (formelle) bevis. Selv om LK20 fremhever at elevene skal engasjeres i prosesser knyttet til søk etter likheter og ulikheter, er det i de fleste tilfeller som omhandler konkrete matematiske sammenhenger, ikke gjort eksplisitt i læreplanen om det man kommer frem til bør valideres.

LK20 inneholder generelle formuleringer om at det skal argumenteres for løsninger og sammenhenger, noe som gir mulighet til lærere å kunne fortsette prosesser med søk etter likheter og ulikheter frem mot validering. I tillegg er det en del formuleringer som peker på konkrete sammenhenger som skal forklares eller argumenteres for. Dermed gir LK20 mange muligheter til arbeid med argumentasjon. Argumentasjon og bevis er, slik Jeannotte og Kieran (2017) bruker begrepene, definert med økende grad av deduktiv struktur og stringens, noe som innebærer at ikke all argumentasjon kan betraktes som bevis, den må oppfylle noen krav. Ifølge definisjonen av argumentasjon i LK20, «handlar [argumentasjon] om at elevane grunngir framgangsmåtar, resonnement og løysingar og beviser at desse er gyldige». Slik sett kan det tolkes at all argumentasjon som nevnes i LK20 skal være bevis, selv om begrepet bevis nevnes bare i denne ene formuleringen i LK20. For at argumentasjon skal kunne betraktes som bevis innebærer det at argumentet er deduktivt og at det er tydelig hva det bygger på (aksepterte sannheter) (Jeannotte & Kieran, 2017). For å utvikle deduktiv tenking er det nødvendig at elever får muligheter til å arbeide med logikk og formelle aspekter i matematikk. Våre funn (Log-kategorien i tabell 1) viser at slike muligheter i liten grad er gjort eksplisitte i den nye læreplanen. Når det gjelder elevers arbeid med matematiske definisjoner (Defn-kategorien), finner vi at LK20 inneholder formuleringer som kan omhandle det. Likevel er formuleringene i Defn-kategorien nokså uformelle og handler ikke eksplisitt om forståelsen for rollen til definisjoner (men heller bruk av matematiske begreper), noe som kan medføre manglende muligheter for elever til å utvikle kompetansen knyttet til måten man bruker definisjoner i bygging av et deduktivt argument.

Kompetansen knyttet til å ta i bruk ulike sammenhenger, relasjoner og representasjoner (tilhørende i Struct-kategorien) er også en viktig del av bevisrelaterte kompetanser slik Hemmi et al. (2013) diskuterer. Den bidrar til bredere grunnlag som kan brukes som utgangspunkt i utforming av et bevis, altså som aksepterte sannheter. Evnen til å ta i bruk og veksle mellom representasjoner vil også være viktig for å kunne presentere bevis på en matematisk gyldig måte som er tilpasset til en gitt elevgruppe. Som tabell 1 viser, gir LK20 muligheter til arbeid med ulike sammenhenger, relasjoner og representasjoner, noe som kan støtte opp om arbeid med bevis.

Vi konkluderer med at LK20 gir muligheter for at elevene skal arbeide med å søke etter likheter og ulikheter slik Jeannotte og Kieran (2017) definerer disse prosessene, og dermed komme frem til påstander om relasjoner mellom og egenskaper til matematiske objekter. Ved at det stadig brukes generelle formuleringer om at elevene skal argumentere for tankegang, fremgangsmåter og sammenhenger, åpnes det for at undervisningen kan gå videre i resonneringsprosessen til arbeid med å validere påstandene som er blitt konstruert. Ifølge læreplanen skal elevene arbeide med ulike representasjoner og sammenhenger som kan være nyttige i arbeid med validering. På den andre siden peker manglende fremheving av bevis og det å bevise, manglende fokus på logikk og formelle aspekter av matematikk, og manglende fremheving av rollen av matematiske definisjoner på at læreplanen ikke legger til rette for at argumentasjon det jobbes med, utvikles til bevis. Som tidligere diskutert definerer LK20 argumentasjon i matematikk til å være at det «handlar om at elevane grunngir framgangsmåtar, resonnement og løysingar og beviser at desse er gyldige» (vår utheving), og slik sett gis det mulighet for å jobbe med bevis gjennom hele grunnskolen. Likevel kan manglene knyttet til kategoriene Proof, Defn og Log gjøre det vanskelig.

Selv om LK20 åpner for muligheter for at elever skal utvikle flere bevisrelaterte kompetanser gjennom grunnskolen (Invest, Arg og Struct), ser vi at mye er overlatt til lærebokforfattere og lærere. Utforsking der man søker etter mønster og sammenhenger og kommer frem til en beskrivelse av det man ser, uten å prøve videre å finne ut hvorfor og når sammenhenger oppstår eller er gyldige, kan virke negativt inn på elevers beviskompetanse og det å se på arbeid med matematikk som å skape mening. Flere forskere har pekt på de problemene elever har i overgangen fra grunnutdanning til videregående utdanning der de plutselig må bevise matematiske utsagn, en aktivitet som er fremmed for dem (se f.eks. Ball et al., 2002).

Vi får håpe at mulighetene den nye læreplanen gir til å arbeide med matematisk resonnering og bevis blir tatt vare på av lærebokforfattere og lærere.

Avslutning

Det som står i en læreplan, kan tolkes og realiseres i undervisning på mange ulike måter. For å si noe om elevers muligheter for å lære er det alltid viktigere å analysere hva som skjer i klasser enn hva som står i en læreplan. Likevel legger læreplaner premisser for læreres undervisningsarbeid, utvikling av læremidler, og skolenes og lærerutdanningenes utforming av profesjonell utvikling. Derfor er det viktig å analysere muligheter og utfordringer for elevers læring og kompetanseutvikling som kan ligge i en læreplan. I denne studien har vi identifisert hvordan matematiske kompetanser relatert til arbeid med bevis fremkommer i læreplanen LK20 for norsk grunnskole. I videre studier kan det være viktig å finne ut hvordan arbeidet med de bevisrelaterte kompetansene spilles ut i lærebøker og i skolen.

I tillegg til analysen av læreplanen ser vi på vår bruk av Jeannotte og Kierans (2017) modell av matematisk resonnering i kombinasjon med kategoriseringen av bevisrelaterte kompetanser til Hemmi et al. (2013) som viktige bidrag til forskningsfeltet. Ved å se de to rammeverkene i sammenheng (som illustrert i figur 1) kommer betydningen de ulike bevisrelaterte kompetansene kan ha for arbeid med bevis, tydelig frem. Denne tydeliggjøringen av betydningen av de ulike bevisrelaterte kompetansene kan bidra til større bevisstgjøring av både forskere, lærere og lærerutdannere omkring betydningen av arbeid med ulike aktiviteter og aspekter ved bevis.