Undervisningskvalitet og elevenes læring
I TIMSS 2015-studien ble det tatt et norsk initiativ for å utvide elevspørreskjemaet med spørsmål relatert til undervisningskvalitet i matematikktimene. Analyser av disse dataene viser at viktige aspekter ved undervisningskvalitet har positiv sammenheng med elevenes læringsresultater.
Forskning viser at kvaliteten på lærerens undervisning er den viktigste enkeltfaktoren for å styrke elevers læringsutbytte (Klette, 2013). Men hva kjennetegner egentlig «god undervisning»? Hvordan kan dette begrepet avgrenses og måles på en meningsfull måte og samtidig relateres til elevenes læring? Selv om undervisningskvalitet er blitt definert på ulike måter innenfor pedagogisk og didaktisk forskning, er det bred enighet om at begrepet har flere aspekter eller dimensjoner. I TIMSS 2015 måles undervisningskvalitet ut fra følgende fire dimensjoner:
- klasseledelse
- støttende lærer
- tydelige intensjoner
- kognitive utfordringer
Særlig forskningsarbeidene til Klieme et al. (2009) og Baumert et al. (2010) har vært viktige i arbeidet med å utvikle disse fire dimensjonene. I punktene under gis det en kort forklaring på hvordan de kan forstås.
Klasseledelse handler om lærerens evne til å skape et klasseromsmiljø med god orden og effektiv tidsbruk. Denne dimensjonen har i tidligere studier vist seg enklest å måle.
Støttende lærer innebærer at læreren gir ekstra hjelp når dette er nødvendig, evner å lytte til elevene, respekterer deres spørsmål og oppfatninger, oppmuntrer elevene og gir dem emosjonell støtte.
Tydelige intensjoner er relatert til lærerens evne til å tydeliggjøre læringsmål, knytte ny kunnskap til det elevene allerede kan, og gi en kort oppsummering ved avslutningen av arbeidsøkten.
Kognitive utfordringer er relatert til elevoppgavenes utforming, kvaliteten på klasseromsdiskusjonene, nivået på det faglige innholdet som gjennomgås i timene, og til undervisningsaktiviteter hvor elevene skal evaluere, integrere eller anvende kunnskap for å løse gitte problemer. Kognitive utfordringer har vist seg spesielt vanskelig å måle på generell basis, uten å knytte det opp mot et spesifikt fag. Også det sistnevnte byr imidlertid på utfordringer.
Alle aspekter ved undervisningskvalitet måles ikke gjennom disse fire dimensjonene. Det å modellere, gi elever konstruktive tilbakemeldinger og lede klasseromsdiskusjoner på en god og inkluderende måte er for eksempel viktige elementer i en dyktig lærers undervisningsrepertoar. Men dimensjonene som brukes i TIMSS 2015-studien, dekker likevel mange viktige aspekter av begrepet undervisningskvalitet.
Måling av undervisningskvalitet i TIMSS
TIMSS-elevene rapporterer om sin egen matematikklærers undervisningskvalitet gjennom å svare på spørsmål i et elevspørreskjema, og man innhenter data fra alle elevene i klassen. Dataene blir så aggregert til klassenivå, og sammenhengen mellom undervisningskvalitet og for eksempel prestasjoner blir analysert på både elev- og klassenivå samtidig. Dette gir muligheter for å kontrollere for forskjeller mellom elevenes svar, og man oppnår et mer robust mål for undervisningskvalitet.
I de norske elevspørreskjemaene for TIMSS 2015, det vil si både for barnetrinnet og ungdoms-trinnet, var det fra fem til sju spørsmål knyttet til hver av de fire dimensjonene av undervisningskvalitet. Disse spørsmålene er teoribaserte og utprøvd i tidligere studier (Klieme et al, 2009; Baumert et al. 2010).
Hva elevene svarer
I figur 1 presenteres gjennomsnittsverdiene for begge trinn på enkeltspørsmålene som inngår i dimensjonen klasseledelse. Svaralternativene var: Hver time (3); De fleste timer (2); Noen timer (1); Aldri eller nesten aldri (0). Skalaen som er brukt, er altså firedelt, med verdiene 0, 1, 2 og 3, slik som det her er angitt i parentesene. Dersom elevene hadde fordelt seg likt på de fire svaralternativene, ville gjennomsnittsverdien blitt 1,5.
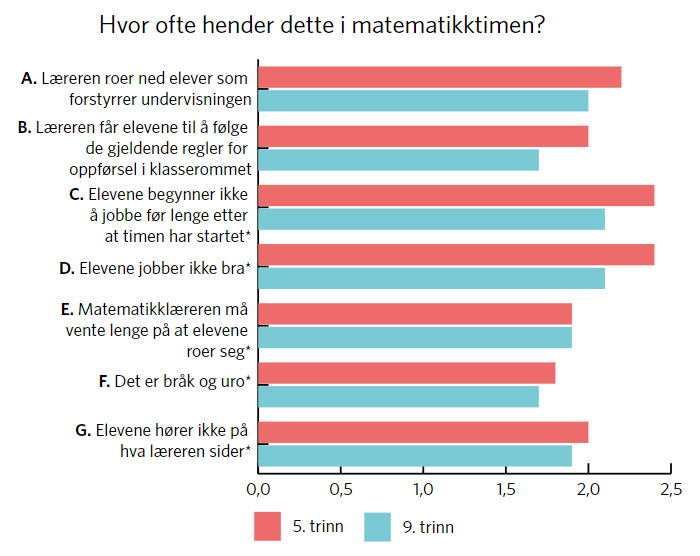
Som det går fram av figur 1, tenderer 5.-trinnselever mot å gi noe mer positive svar enn 9.-trinnselever, men dette anses først og fremst å være relatert til holdningsforskjeller til skole, betinget av alder. Gjennomsnittsverdiene for alle spørsmålene er høyere enn 1,5, noe som viser at elevene generelt rapporterer positivt om matematikklærerens klasseromsledelse.
Figur 2 viser gjennomsnittsverdiene for spørsmålene som inngår i dimensjonen støttende lærer. Svaralternativene var de samme som for klasseledelse. Gjennomsnittsverdiene er jevnt over høye.
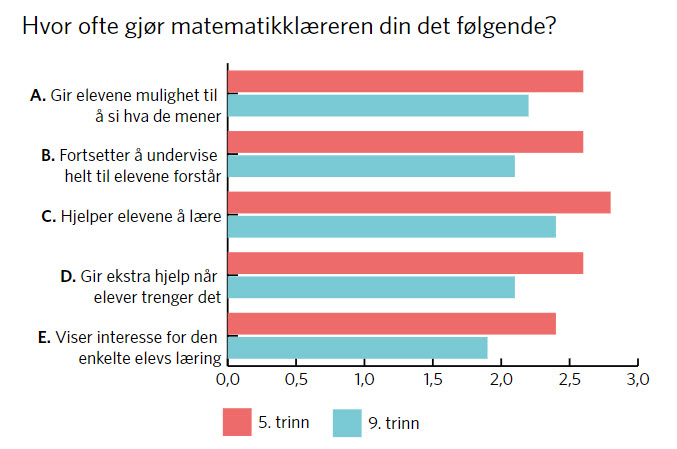
Elevene på begge trinn vurderer altså matematikk-læreren sin svært positivt på denne dimensjonen.
I figur 3 presenteres gjennomsnittsverdier for spørsmålene som inngår i dimensjonen tydelige intensjoner. Elevene fikk de samme svaralternativene. Her er det litt større forskjeller mellom gjennomsnittene for enkeltspørsmålene. Gjennomsnittet for oppsummeringer er lavest.
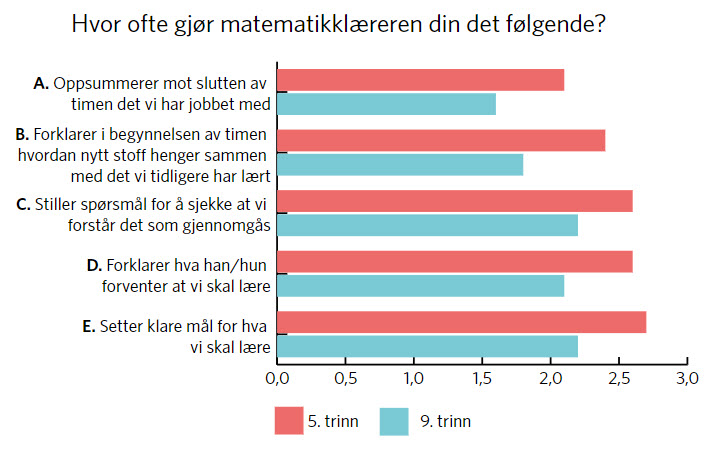
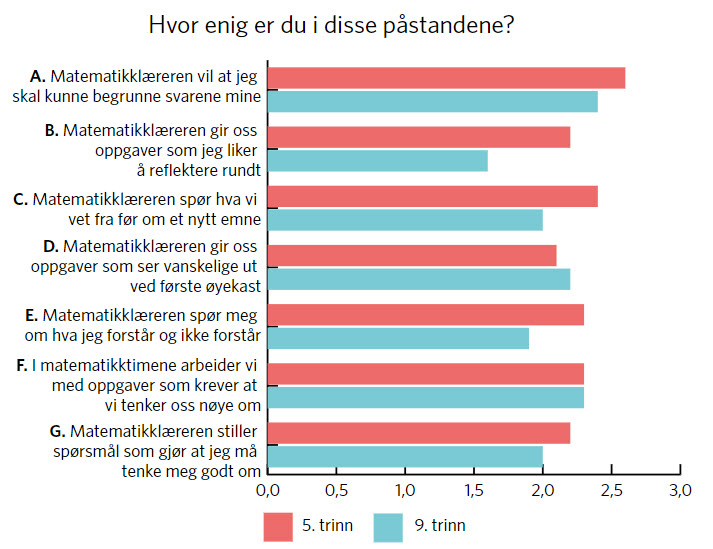
Figur 4 viser gjennomsnittsverdier for spørsmålene som utgjør dimensjonen kognitive utfordringer. Her var svaralternativene: Svært enig (3); Litt enig (2); Litt uenig (1); Svært uenig (0). På flere av spørsmålene er det små forskjeller i gjennomsnittsverdier mellom de to trinnene. Det å måtte begrunne svarene sine er ett av disse (spørsmål A), og dette spørsmålet har høyest gjennomsnittsverdi på begge trinn. Gjennomsnittsverdiene for spørsmålene knyttet til oppgavenes vanskelighetsgrad, og til det «å tenke seg nøye/godt om» (spørsmål F og G), er også relativt like. Den aller største forskjellen i gjennomsnittsverdier mellom trinnene er på spørsmål B, som er nært relatert til holdninger til matematikk. Dette harmonerer godt med tidligere forskning som viser at elever på barnetrinnet har mer positive holdninger til matematikk enn elever på ungdomstrinnet (Vella, 2011).
«Undervisningskvalitet» og læringsutbytte
Hva er så sammenhengen mellom undervisningskvalitet og læringsutbytte? Kan man med bakgrunn i analyser av TIMSS 2015-data hevde at god undervisningskvalitet har positiv sammenheng med elevenes læringsutbytte, slik dette måles i TIMSS?
I våre analyser måles altså samlevariabelen undervisningskvalitet gjennom de fire dimensjonene: klasseledelse, støttende lærer, klare intensjoner og kognitive utfordringer. Videre undersøkes sammenhengen mellom .
Analysene viser at undervisningskvalitet har en positiv og signifikant (p< 0,05) sammenheng med prestasjoner på 5. trinn. Regresjonskoeffisienten er 0,35, noe som kan betegnes som en middels stor koeffisient. Tilsvarende analyser for 9. trinn gir et . Dette indikerer at det er en signifikant og positiv sammenheng mellom undervisningskvalitet og prestasjoner på disse trinnene.
TIMSS sammenlignet med norske klasseromsundersøkelser
Analyser av data fra TIMSS 2015 viser at undervisningskvalitet har en positiv og signifikant sammenheng med elevprestasjoner i matematikk, både på 5. trinn og 9. trinn. Det vil si at i klasser hvor lærerens undervisning holder høy kvalitet, tenderer elevenes læringsutbytte til å være høyere enn i klasser hvor undervisningen er av lavere kvalitet. Disse funnene er i tråd med tidligere forskning, hvor lignende sammenhenger er påvist.
TIMSS er den eneste av de internasjonale storskalaundersøkelsene som har data på klassenivå, og samtidig mål på elevers prestasjoner. Det er en styrke ved TIMSS-studien at man har muligheten til å se på sammenhenger mellom undervisning og læringsresultater (Nilsen & Gustafsson, 2016). Når TIMSS dessuten har representative utvalg av elever, kan man generalisere funn til hele populasjonen som utvalget er trukket fra. I mindre case-studier eller klasseromsstudier vil dette ikke kunne gjøres, siden disse ikke opererer med representative utvalg. Slike studier har derimot sin styrke i direkte observasjoner av aktivitetene i klasserommet. Dette kan forskere gjøre ved selv å være til stede i klasserommet, ved å analysere videoopptak av undervisning eller ved å kombinere disse to observasjonsmåtene. En fordel er at man da kan benytte egne kategorier i analysene av undervisning og læring. Det er uansett svært interessant å undersøke om funnene som nå er presentert fra TIMSS 2015-studien, samsvarer med funn fra norske video- og klasseromsstudier.
Fra norske video- og klasseromsstudier (Klette, Blikstad-Balas & Roe, 2017; Streitlien, 2009; Skorpen, 2006) rapporteres det at undervisningen i matematikk kjennetegnes ved at det:
- er gode elev–lærerrelasjoner
- er god ledelse og orden i klasserommet
- brukes mye tid til helklasseundervisning, og at denne skjer i dialog med elevene
- brukes mye tid til individuell oppgaveløsing med oppgaver hentet fra læreboka
- brukes relativt lite tid til å arbeide med kognitivt utfordrende oppgaver og problemstillinger
- legges relativt liten vekt på introduksjoner og oppsummeringer av aktiviteter
Ikke alle disse punktene dekkes av elevspørreskjemaet i TIMSS. Men norske klasseromsstudier viser altså at lærere har en god hånd med klasseromsledelse, og at det er svært gode elev–lærerrelasjoner. For dimensjonene god klasseromsledelse og støttende lærer synes det derfor å være stor overensstemmelse mellom TIMSS-elevenes vurderinger og klasseromsforskernes rapportering. Hva så med de to andre dimensjonene: klare intensjoner og kognitive utfordringer? Det kan ved første øyekast synes som om det her er betydelige uoverensstemmelser, ettersom TIMSS-elevene her gir mer positive vurderinger enn klasseromsforskerne. Ser man nærmere på enkeltspørsmålene som elevene besvarer i TIMSS, finner man imidlertid at elevene for dimensjonen tydelige intensjoner rapporterer minst positivt på spørsmålene knyttet til introduksjoner og oppsummering av fagstoff (spørsmål A og B i figur 3). Nettopp mangel på systematisk bruk av introduksjoner og oppsummeringer i matematikktimene har vært et tema som klasseromsforskere på bakgrunn av sine observasjoner har drøftet i flere publikasjoner (Klette et al., 2008; Skorpen, 2006).
Når det gjelder dimensjonen kognitive utfordringer, har det i oppsummeringer av funn fra klasseromsstudier blitt pekt på at kognitivt utfordrende oppgaver i matematikk blir for lite brukt (Kunnskapsdepartementet, 2015). Dette har blant annet blitt knyttet til lærebokas dominerende posisjon og liten bruk av det som ofte betegnes som «rike oppgaver» eller «problemløsningsoppgaver» (Kunnskapsdepartementet, 2015). Disse funnene støttes av forskning publisert fra video-/klasseromsstudien LISA (Klette, Blikstad-Balas & Roe, 2017). Her rapporterer forskerne om at de blant annet observerer mindre bruk av kognitivt utfordrende aktiviteter i de norske klasserommene enn i de finske (Klette, Roe & Luoto 2017). Det kan umiddelbart synes som om funnene innenfor denne dimensjonen harmonerer dårlig med det tilsvarende positive bildet som tegnes av elevene i TIMSS 2015-studien. Hva kan dette skyldes?
Spørsmålene som benyttes for å måle kognitive utfordringer i elevspørreskjemaet i TIMSS, er naturlig nok tilpasset de aktuelle aldersgruppene og kan derfor ikke direkte sammenliknes med klasseromsforskernes eller fagdidaktikeres kategorier på dette feltet. Det ville for eksempel ikke gi mening å spørre elevene om hvorvidt de arbeidet mye med «rike oppgaver» eller «problemløsningsoppgaver», da dette er en type fagterminologi som hovedsakelig benyttes av forskere. Når elevene gir uttrykk for at de opplever matematikk som kognitivt utfordrende, er dette knyttet til at mange elever faktisk må tenke seg godt om for å løse oppgavene de møter i matematikktimene. Spørsmålene i TIMSS som elevene besvarer, måler altså litt andre aspekter av faglige og kognitive utfordringer enn det som omtales av klasseromsforskerne. Samtidig illustrerer dette at vi trenger både kvantitative og kvalitative data for å øke vår forståelse av prosesser i klasserommet og for å kunne peke på hvilke faktorer som henger sammen med god læring. I Ludvigsen-rapporten (NOU 2015: 8) fremheves det at læringsmiljøer som fremmer læring, kjennetegnes av at elevene får utfordringer som er tilpasset deres faglige nivå, og som gjør at de stadig må strekke seg og bruke sin faglige kompetanse i møte med nye problem-stillinger. En utfordring for kvantitative studier vil være å utvikle spørsmål som også kan måle slike aspekter. Dette ville bidra til å øke validiteten til variabelen «kognitive utfordringer».
På tross av visse forskjeller i begrepsbruk, synes funn fra analysene av undervisningskvalitet i TIMSS å harmonere relativt godt med klasseromsforskernes direkte observasjoner. Dette styrker validiteten til de resultatene som her er presentert. Og disse resultatene peker altså entydig mot at god undervisningskvalitet har positiv sammenheng med elevenes læringsutbytte i matematikk. Hva innebærer så de funnene som her er presentert, for norsk skole og for hvordan man bør tenke rundt undervisning? God klasseromsledelse, klare faglige intensjoner, det å utfordre elevene kognitivt og å opptre støttende overfor elevene er allerede tematisert innenfor lærerutdanning og etter- og videreutdanning av lærere. Håpet er derfor at de analyser og funn som her er presentert, vil stimulere til videre diskusjoner om hvordan man kan strukturere undervisningen og aktivitetene i matematikklasserommet, slik at elevenes læringsutbytte styrkes.
Litteraturhenvisninger
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., et al. (2010). Teachers’ Mathematical Knowledge, Cognitive Activation in the Classroom, and Student Progress. American Educational Research Journal, 47(1), 133–180.
Bergem, O.K., Nilsen, T. & Scherer, R. (2016). Undervisningskvalitet i matematikk. I: O.K. Bergem, H. Kaarstein & T. Nilsen (red). Vi kan lykkes i realfag. Resultater og analyser fra TIMSS 2015. Oslo: Universitetsforlaget.
KD (2015). REALFAG. Relevante – Engasjerende – Attraktive – Lærerike. Rapport fra Ekspertgruppa for realfagene. Oslo: Kunnskapsdepartementet. Lastet ned fra: https://www.regjeringen.no/no/dokumenter/Rapport-fra-ekspertgruppa-for-relafagene/id2343488/
Klette, K. (2013). Hva vet vi om god undervisning? Rapport fra klasseroms-forskningen. I: R.J. Krumsvik & R. Säljö (red.), Praktisk-pedagogisk utdanning: en antologi, 173–201. Bergen: Fagbokforlaget.
Klette, K., Lie, S., Ødegaard, M., Anmarkrud, Ø., Arnesen, N. & Bergem, O. (2008). Rapport om forskningsprosjektet PISA+ (Pluss: Prosjekt om Lærings- og Undervisnings-Strategier i Skole). Oslo: Norges forskningsråd.
Klette, K., Blikstad-Balas, M. & Roe, A. (2017). Linking Instruction and Student Achievement-Research design for a new generation of classroom studies. Acta Didactica, Vol. 11(3). Art. 10. Lastet ned fra: https://www.journals.uio.no/index.php/adno/article/view/4729/4905
Klette, K., Roe, A. & Luoto, J.M. (2017) Comparing Instructional Practices and Student Participation in Finland, Norway and Sweden. Konferanseinnlegg presentert på EARLI, Tampere, Finland, 29 aug.–1. sept. 2017.
Klieme, E., Pauli, C., & Reusser, K. (2009). The Pythagoras Study: Investigating effects of teaching and learning in Swiss and German mathematics classrooms. I: T. Janik & T. Seidel (red.), The power of video studies in investigating teaching and learning in the classroom (137–160). New York: Waxmann Publicing Co.
NOU (2015: 8). Fremtidens skole. Fornyelse av fag og kompetanser. Norges offentlige utredninger.
Nilsen, T., & Gustafsson, J.-E. (red.). (2016). Teacher quality, instructional quality and student outcome. Relationships across countries, cohorts and time. (Vol. 2): Springer.
Nilsen, T. & Kaarstein, H. (2016). TIMSS og statistiske metoder. I: O.K. Bergem, H. Kaarstein & T. Nilsen (red). Vi kan lykkes i realfag. Resultater og analyser fra TIMSS 2015. Oslo: Universitetsforlaget.
Streitlien, Å. (2009). Hvem får ordet og hvem har svaret? Om elevmedvirkning i matematikkundervisningen. Oslo: Universitetsforlaget.
Skorpen, L.B. (2006). Kunnskapstypar og arbeidsformer i matematikk i begynnaropplæringa. I: P. Haug (red.), Begynnaropplæring og tilpassa opplæring – Kva skjer i klasserommet? Bergen: Caspar Forlag.
Vella, D. (2011). Student’s attitudes towards mathematics and its relationship to achievement, gender and age. Lastet ned fra: <https://www.um.edu.mt/library/oar//handle/123456789/3742>