Aspekter ved tallforståelse

Utvikling av tallforståelse framheves i mange studier som svært viktig for elevenes læring av matematikk. Men det er ikke åpenbart hva tallforståelse innebærer. Case (1998) beskriver tallforståelse slik:

Number sense is difficult to define but easy to recognize. Students with good number sense can move seamlessly between the real world of quantities and the mathematical world of numbers and numerical expressions. They can invent their own procedures for conducting numerical operations. They can represent the same number in multiple ways depending on the context and purpose of this representation. They can recognize benchmark numbers and number patterns: especially ones that derive from the deep structure of the number system. They have a good sense of numerical magnitude and can recognize gross numerical errors that is, errors that are off by an order of magnitude. Finally, they can think or talk in a sensible way about the general properties of a numerical problem or expression- without doing any precise computation. (p. 1)

Her fremhever Case fleksibilitet i arbeidet med tall og regneoperasjoner, bruk av ulike representasjoner, utvikling av hensiktsmessige strategier, overslagsregning, identifisering og bruk av ulike mønster, resonnering om egenskaper av tall og operasjoner. McIntosh, Reys and Reys (1992)¹ fremhever i tillegg et emosjonelt aspekt i sin definisjon av tallforståelse:

Number sense refers to a person’s general understanding of number and operations along with the ability and inclination to use this understanding in flexible ways to make mathematical judgments and to develop useful strategies for handling numbers and operations.

Deres definisjon består av tre hovedelementer: "generell forståelse av tall og operasjoner", bruk av denne forståelsen i matematisk resonnering og utvikling av hensiktsmessige strategier i arbeid med tall og regneoperasjoner og lyst til å gjøre det.

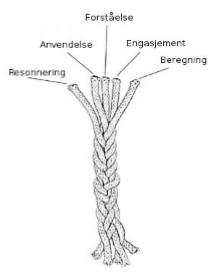
Kilpatrick, Swafford og Findell (2001) beskriver matematisk kompetanse som sammensatt av fem komponenter: begrepsforståelse, beregning, anvendelse (strategisk tankegang), resonnering og engasjement. De fremhever at disse fem komponentene et tett sammenflettet og avhengige av hverandre. Komponentene støtter hverandre, og det er viktig at elevene får mulighet til å utvikle alle fem komponentene samtidig. Forbindelsen mellom de ulike komponentene blir da forsterket og elevene utvikler en matematisk kompetanse som er varig, fleksibel, nyttig og relevant. De fem komponentene finner vi igjen i sitatene om tallforståelse fra Case og McIntosch et al., og denne definisjonen av matematisk kompetanse kan ses som et mulig utgangspunkt for nærmere drøfting av tallforståelse.

Nedenfor presenteres det en kort beskrivelse av de fem komponentene i matematisk kompetanse, og det drøftes ulike aspekter ved tallforståelse innen hver komponent. De ulike aspektene er utviklet gjennom en gjennomgang av forskning som knyttet til arbeid med tall på mellomtrinnet² og analyse av det faglige innholdet i oppgaver som er blitt utviklet for arbeid med tall og regning på mellomtrinnet innen ulike matematikkdidaktiske prosjekter³.

Det er tett sammenheng mellom aspektene ved tallforståelse beskrevet nedenfor. De går delvis inn i hverandre og det er ikke lett å trekke grenser mellom det. Målet med å beskrive tallforståelse i form av noen aspekter er heller ikke å kunne isolere de ulike elementene, men heller fremheve viktige elementer av tallforståelse og gi eksempler på hva de kan gå ut på.

Begrepsmessig forståelse

Begrepsmessig forståelse innebærer å bygge opp begrepsmessige strukturer og se sammenhenger mellom ulike begreper, ideer og prosedyrer. Begrepsmessig forståelse handler også om å tolke, forstå og benytte ulike representasjoner, oversette og veksle mellom ulike representasjoner ut fra hva som kan være nyttig for et gitt formål.   

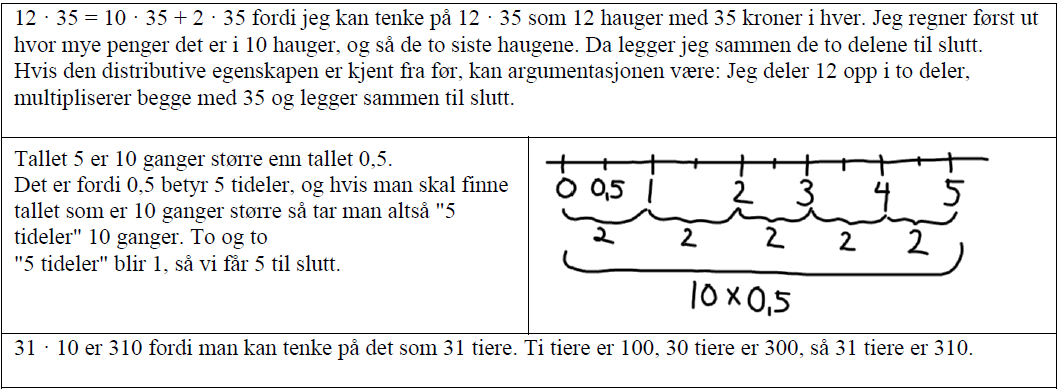
Ulike måter å representere tall på og overganger mellom representasjoner består i å representere positive og negative hele tall, brøk og desimaltall symbolsk, på tallinje, med ulike illustrasjoner, konkreter og regnefortellinger. Det å kunne tolke de ulike representasjonene og veksle mellom dem er av stor betydning for utvikling av tallforståelsen. Eksempler:

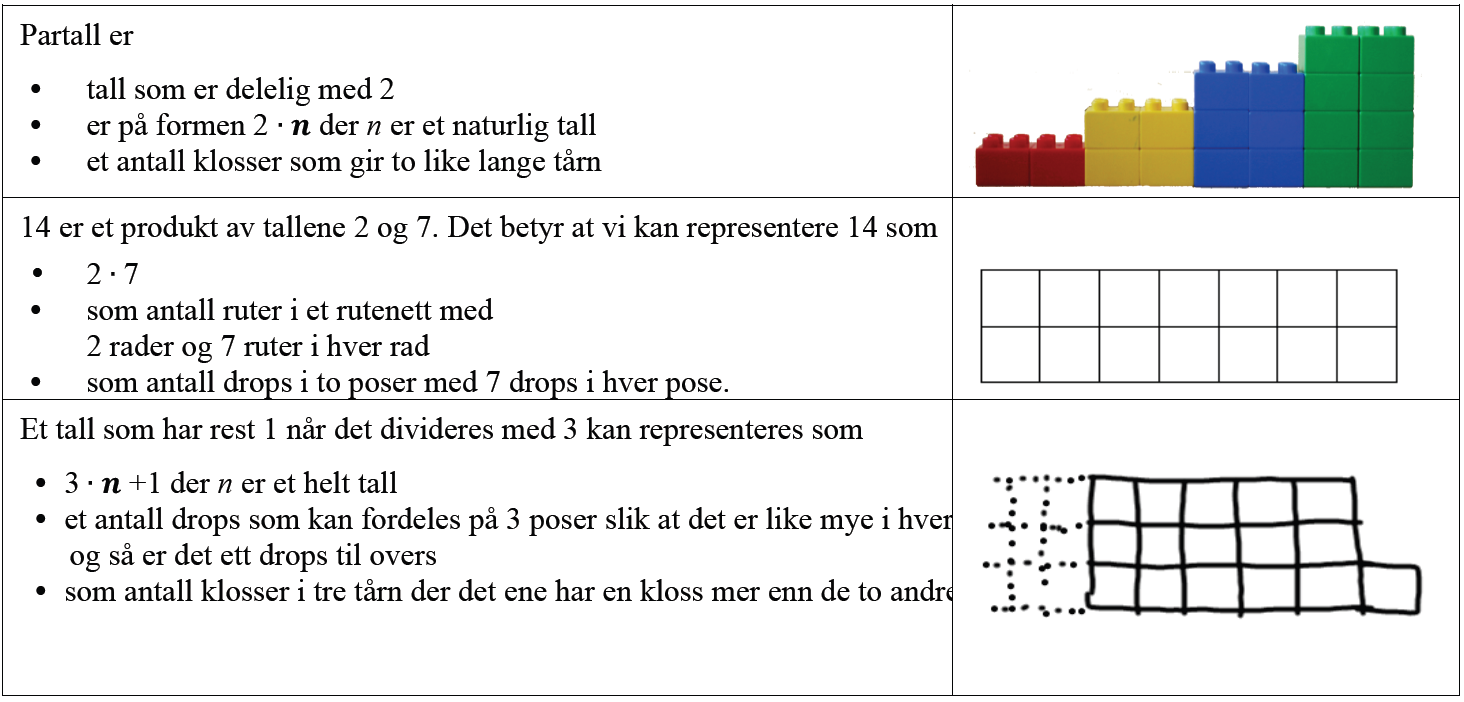
Ulike egenskaper ved tall består i å kjenne til og kunne beskrive egenskaper ved tall, identifisere tall som har egenskapene, beskrive strukturer og representere dem på ulike måter. Eksempler:

Relasjoner mellom tall består i å kjenne til og kunne beskrive ulike relasjoner mellom tall, gjenkjenne relasjonene og representere dem på ulike måter. Eksempler: 

Relasjoner som bygger på posisjonssystemet består i å kjenne til og kunne beskrive ulike relasjoner mellom tall som kommer av posisjonssystemet, fleksibilitet i overgang mellom symboler (tallene skrevet i 10-tallssystemet) og tallverdien. Eksempler:

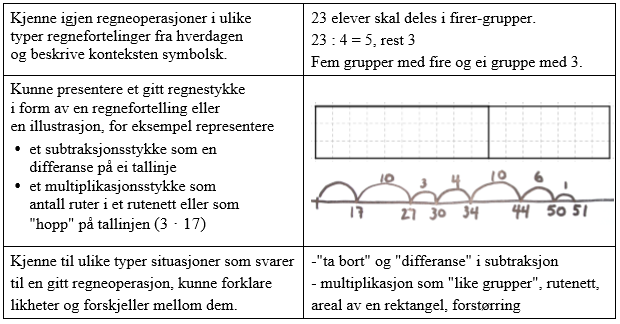
Ulike måter å representere regneoperasjoner på og overganger mellom representasjonene innebærer å kunne representere regneoperasjoner symbolsk, med konkreter og tegninger, på ei tallinje og gjennom regnefortellinger. Det innebærer også å kunne tolke representasjonene og skifte mellom dem. Eksempler:

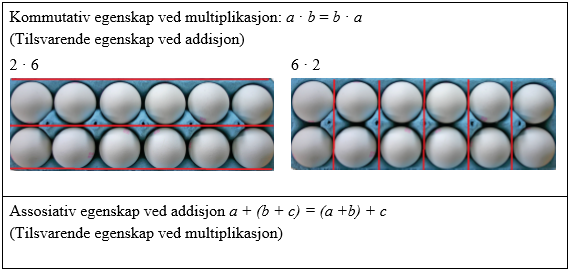
Grunnleggende egenskaper ved regneoperasjoner handler om kjennskap til den kommutative, asssosiative og distributive egenskapen ved regneoperasjoner, kunnskap om motsatte regneoperasjoner og identitetselementer. Det innebærer å kunne uttrykke egenskapene på ulike måter og se sammenhenger mellom dem. Eksempler: 

Beregning

Beregning handler om kunnskap om ulike matematiske prosedyrer/strategier, når og hvordan de kan brukes og å kunne utføre dem nøyaktig, fleksibelt og hensiktsmessig. Det innebærer innsikt i ulike egenskaper ved og relasjoner mellom tall og operasjoner og evnen til å utnytte dem i arbeid med aritmetiske problem. Følgende aspekter kan sees som sentrale når det gjelder beregning.

Utvikling av varierte strategier handler om å kunne utvikle strategier i arbeid med regneoperasjoner. Ofte fremheves betydning av at elever utvikler ulike strategier med utgangspunkt i regnefortellinger og illustrasjoner. Når strategier utvikles på den måten, er det enklere for elevene selv å vurdere hva som kan gjøres og hva som ikke gir mening. Overganger mellom de ulike representasjonene er av stor betydning i denne utviklingen. Hvis en strategi utvikles for eksempel gjennom en regnefortelling, er det viktig at den også beskrives symbolsk. Det kan virke til at en bevissthet om fremgangsmåten generaliseres utover den gitte konteksten. Arbeid med tallmønster kan også være utgangspunkt for utvikling av variere strategier. Eksempler:

 
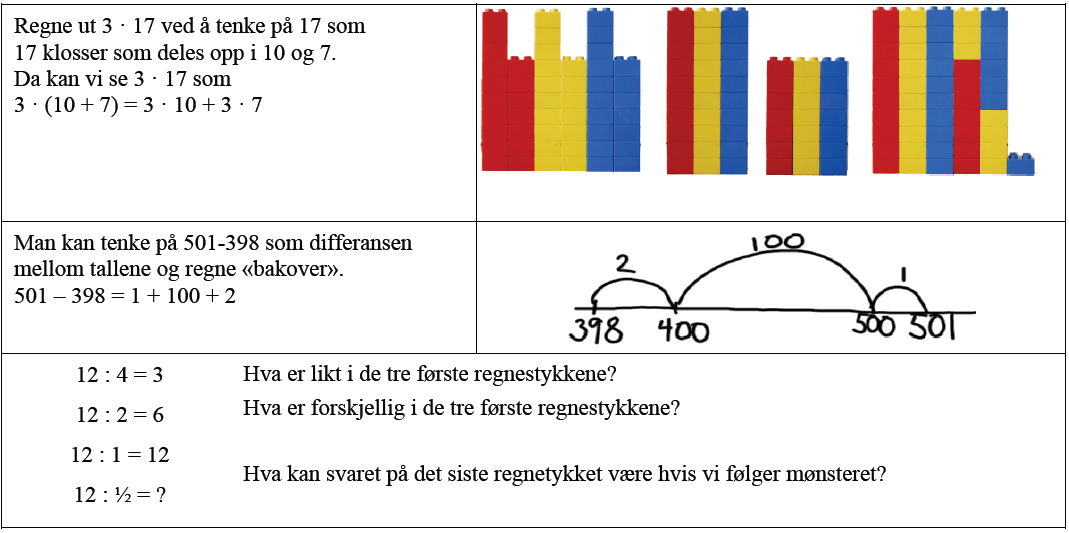
Bruk av varierte strategier består i å beherske ulike skriftlige og muntlige strategier i arbeid med tall og regneoperasjoner, kunne bruke estimering og digitale hjelpemidler. I denne artikkelen skilles det ikke spesielt mellom muntlige og skriftlige strategier, siden det gjerne er den samme tenkingen som ligger i bunn og det avhenger av tallene om det kan være nødvendig å notere noe underveis. I de ulike regnestrategiene er det forskjellige egenskaper ved tall, posisjonssystemet og operasjoner som utnyttes. Eksempler:

Valg av en hensiktsmessig strategi handler om å kunne vurdere hvilken strategi som kan være hensiktsmessig for det gitte regnestykket og for den gitte situasjonen. Selv om det kan være mange fremgangsmåter for å finne svar i et gitt regnestykke, er gjerne noen strategier mer hensiktsmessige enn andre for akkurat de gitte tallene.

I mange situasjoner, spesielt de som er knyttet til dagliglivet, er det heller ikke så viktig med et helt nøyaktig svar, det holder med et estimat. Videre, i situasjoner der nøyaktig svar er viktig, der utregninger ikke står i fokus og der tallene er ”lite pene”, kan bruk av kalkulator være mest hensiktsmessig. Eksempler:

Effektivitet og nøyaktighet er viktige elementer i arbeid med regneoperasjoner. Arbeid med matematiske problem krever ofte en del utregninger, og det kan være greit at man etter hvert kan utføre dem uten å være nødt til å tegne og telle. Effektivitet og nøyaktighet i beregning bygger på automatisering av enkle tallfakta, et spekter av referansetall og et bredt utvalg av strategier man kan velge mellom.

Automatisering av enkle tallfakta som 9+5 = 14 og 12·10 =120 viktig for videre arbeid med tall, men det er viktig at læringen ikke handler om ren memorering. Erfaringer med tallfakta i ulike situasjoner, gjennom ulike representasjoner og med fokus på strukturer og relasjoner vil etter hvert føre til automatisering. Erfaringer med ulike strategier og diskusjoner om hvilke som kan være hensiktsmessige i en gitt situasjon, kan legge til rette for en gradvis effektivisering av valg av strategi for å løse et gitt problem og utnyttelsen av faktakunnskap. Eksempler:

 

Anvendelse eller strategisk tankegang

Anvendelse eller strategisk tankegang innebærer å kunne gjenkjenne og formulere matematiske problemer, representere dem på en hensiktsmessig måte, utvikle en løsningsstrategi og vurdere hvor rimelig løsningene er. Med matematiske problemer menes det her problem i hverdags-, arbeids- og samfunnsliv der matematikk kan anvendes, men også abstrakte matematiske problem og spørsmål. Kjennetegnet på et "problem" er at man ikke har opparbeidet en rutine for å løse det. Man trenger å utvikle en strategi for å løse problemet. Dette innebærer at det som er et problem for noen ikke trenger å være det for noen andre. Eksemplene i det følgende må betraktes ut fra denne forståelsen av problem. 

Gjenkjenning og formulering av matematiske problem innebærer å gjenkjenne situasjoner der ulike begreper og ideer knyttet til tall og talloperasjoner kan brukes til å beskrive situasjonen og formulere et matematisk problem eller hypotese. Innhenting av nødvendig informasjon, kvantifisering av ulike størrelser og valg av variabler man skal se på også viktige elementer her. Eksempler:

Utvikling av en løsningsstrategi for et matematisk problem består i å kunne representere problemet på ulike måter og knytte det til kunnskap om tall, regneoperasjoner og kjente sammenhenger og fremgangsmåter. Videre består det i å kunne utforske problemet systematisk og søke etter mønster eller system. For å få bedre innsikt i ulike sider ved problemet kan det være nyttig å skifte mellom ulike representasjoner. Eksempler:

Vurdering av svar dreier seg om å overveie størrelsene og se for seg situasjonen, tenke gjennom om svaret kan være rimelig. Det innebærer også å tenke gjennom om det er noe som kan ha betydning for beregningene og som det ikke er tatt hensyn til under arbeidet. Eksempler:

Resonnering

Resonnering handler om å kunne forklare hvordan man tenker, se etter mønster og sammenhenger. Videre handler det om å utforme hypoteser, begrunne sammenhenger mellom ulike begreper, egenskaper og framgangsmåter og følge med i andres resonnement. Det innebærer også å kunne argumentere for gyldigheten av en hypotese ved å utforme et resonnement med utgangspunkt i noe som er kjent og å stake ut veien mot det som er ukjent og skal undersøkes.

Innen tallforståelse handler resonnering om ulike sammenhenger og egenskaper ved tall og regneoperasjoner, og man kan skille mellom det å resonnere om og begrunne noe for et enkelt eksempel eller for en klasse eksempler (generalisering). 

Gjenkjenning og beskrivelse av struktur, mønster og sammenhenger i arbeidet med tall består i å søke etter og beskrive mønster og sammenhenger. Dette er det første steget i resonnering, utforming av hypoteser og utforskning. Eksempler:

 

Begrunnelser av strategi/sammenheng på enkelteksempler består både i å kunne begrunne og kommunisere egne resonnement om enkelteksempler og å kunne følge med i andres begrunnelser. Eksempler:

Utforskning av generelle hypoteser ved bruk av et generisk eksempel eller et moteksempel. Når vi bruker et generisk eksempel ser vi på et enkelteksempel "på en generell måte". Ved å resonnere undersøker vi om noe ville blitt annerledes med andre eksempler av samme type. Ofte kan det være formålstjenlig å bruke en regnefortelling eller modell for å se hva som skjer og hvorfor det blir slik.

Resonnering om grunnleggende egenskaper ved regneoperasjoner er for eksempel vanskelig uten å ta i bruk en annen representasjon enn symboler. Bruk av ulike representasjoner kan generelt være viktige for elevers resonnering og utforskning av generelle sammenhenger. Moteksempler er også viktige i utforskning av generelle hypoteser. Eksempler:

Utforske gyldigheten av generelle hypoteser ved utforming av generelle resonnement. Generelle hypoteser kan også undersøkes generelt, ikke bare ved generiske eksempler eller moteksempler som vist over. Generelle resonnement bygger på kjente resultater og gjerne ved å ta i bruk algebraisk notasjon, men det er ikke alltid nødvendig. Eksempler:

Engasjement

Engasjement handler om å se matematikk som fornuftig, nyttig og verdifull. Videre innebærer dette aspektet å ha tro på at det er mulig bli kompetent i matematikk og at man lærer ved å streve og ikke gi opp.

Ha tro på at innsats fører til læring handler om å se seg selv som en som kan lære matematikk. Utvikling av kompetansen til å gjenkjenne og bruke ulike relasjoner, utvikle varierte strategier i arbeid med tall og aritmetiske operasjoner, utforme og begrunne hypoteser osv. tar tid og krever innsats og konsentrasjon, men det er mulig for alle.

Oppleve det som meningsfullt å søke etter relasjoner i arbeidet med tall handler om at elevene bør få erfare at det å se etter sammenhenger og strukturer gir mening og gjør faget kreativt og skapende. Mønstrer og sammenhenger er selve kjernen i matematikk. Søk etter mønster og sammenheng kan gjøre tilsynelatende kjedelige regnestykker til utgangspunkt for spennende og kreative måte å tenke på og å utfordre seg selv på.

Se det som nyttig å bruke ulike representasjoner i arbeidet med tall. Ulike representasjoner gir innblikk til ulike egenskaper og aspekter ved et tall. Noen ganger kan det passe bedre å representere tallet på en spesiell måte enn en annen måte. Noen ganger representerer vi tallet seks som symbolet "6", andre ganger som 4 + 2 eller 3 · 2. I noen tilfeller kan det være lurt å tenke på det som et punkt på tallinja, i andre tilfeller som en mengde på 6 eller som en lengde på 6. En bevissthet om muligheter til representere tall, operasjoner, egenskaper osv. på ulike måter og verdien av å bruke det er viktig for elevers læring.

Se verdien av å utvikle flere fremgangsmåter for samme type problem. Ulike fremgangsmåter og sammenligning av dem gir mulighet til å se et problem fra ulike sider. Det gir også mulighet for å tenke kreativt, velge hensiktsmessige fremgangsmåter og å etablere relasjoner mellom ulike ideer. Elevene bør se på disse elementene som viktige i arbeid med ulike problem knyttet til tall og regneoperasjoner. Som oftest er dette være viktige for matematikklæring enn selve svaret i et gitt problem.

Utvikling av tallforståelse

De fem komponentene – begrepsmessig forståelse, beregning, anvendelse (strategisk tankegang), resonnering og engasjement – og aspektene ved hver av dem er tett sammenflettet og avhengige av hverandre. De støtter hverandre, og de utvikles samtidig. Det betyr at det ikke er slik at ”bare elevene blir flinke til å regne, så kommer forståelsen etter hvert”, noe man ofte kan høre.

”Flink til å regne” innebærer mye mer enn å memorere noen tallfakta og kunne følge et gitt oppsett. Utvikling av strategier henger tett sammen med forståelse av relasjoner mellom tall og operasjoner, ulike representasjoner, begrunnelser for strategier og verdsetting av ulike måter å tenke på. Tilsvarende med alle andre aspekter av tallforståelse; de utvikles sammen, forsterkes av hverandre og kan ikke tenkes i en rekkefølge.

En oppgave legger gjerne opp til noen aspekter i større grad enn noen andre, og det kan være viktig at læreren også velger hvilke aspekter hun ønsker å fremheve under arbeidet med en gitt oppgave. Men det er viktig at alle de ulike aspektene arbeides med over tid. Elevene utvikler da en tallforståelse som er varig, fleksibel, nyttig og relevant både for videre matematikklæring, i deres hverdagsliv og seinere i deres profesjonelle karriere.

Bevissthet og metakognisjon er sentrale aspekter ved matematikklæring generelt, og også i utvikling av tallforståelse. Elever som får arbeide med tallforståelse med utgangspunkt i denne forståelsen av trådmodellen vil implisitt utvikle både bevissthet og metakognisjon. Men det er også viktig å diskutere utvikling av kompetansene eksplisitt med elevene. Spesielt vil aspekter ved engasjement kunne forsterkes gjennom eksplisitt diskusjon med elevene om hva matematikk handler om og hvordan man lærer matematikk.

Verdien av representasjoner og nyttighet av å utvikle flere fremgangsmåter må inngå i denne prosessen. Diskusjoner der man "ser ovenfra" på arbeid med tall og regneoperasjoner og diskuterer hva, hvordan og hvorfor kan bidra til økt motivasjon og bedre prestasjonen i faget.