Kartlegging av læreres kunnskap er ikke enkelt

De siste tiårene har det vært økt fokus på den kunnskapen lærere trenger for å undervise i matematikk. Mens foreldre og elever stort sett er fornøyde med lærernes kunnskap (Opsal & Topphol, 2011), ser ikke våre politiske ledere ut til å være enige. I 2007 skrev daværende statsminister Jens Stoltenberg i en kronikk at en av utfordringene i norsk skole, slik han så det, var at elever lærte for lite matematikk. Årsaken mente han kunne ligge i lærernes kunnskap. Argumentasjonen til Stoltenberg var delvis basert på resultater fra internasjonale studier som PISA¹ (Kjærnsli, Lie, Olsen & Roe, 2007) og TIMSS² (Grønmo & Bergem, 2009). I senere tid har flere forskere kritisk diskutert hva en kan, og ikke kan, bruke resultatene fra slike studier til. Et eksempel er Sjøberg (2014), som argumenterte for at PISA og TIMSS ikke nødvendigvis er egnet til å trekke konklusjoner i den retning Stoltenberg gjorde i sin kronikk. Vår nåværende statsminister Erna Solberg, er likevel enig med sin forgjenger på akkurat dette punktet. Basert på senere PISA-resultater (Kjærnsli & Olsen, 2013), sa hun i et intervju at norske lærere ligger dårlig an. Hun konkluderte med å peke på betydningen av en kartlegging av læreres tilsynelatende manglende kunnskap (Ertesvåg, 2013). I skrivende stund har NOKUT på oppdrag fra kunnskapsminister Torbjørn Røe Isaksen utviklet en prosjektplan for nasjonale deleksamener for lærerstudenter, og kunnskapsministeren har i andre sammenhenger indikert at kartlegging av nyutdannede læreres kunnskap også er aktuelt.

Måling av den kunnskapen lærere trenger for å undervise i matematikk er imidlertid ikke det samme som å måle elevers kunnskaper i matematikk. Mens elevene skal tilegne seg en allmenn matematisk kunnskap, er læreres undervisningskunnskap i matematikk mer sammensatt. Da Shulman (1986) presenterte sine teorier om læreres profesjonskunnskap, var noe av hovedbudskapet at den kunnskapen lærere trenger for å utøve sin profesjon er spesialisert og sammensatt. I kjølvannet av Shulmans forskning har det blitt utviklet flere ulike modeller og instrumenter for å beskrive og måle ulike aspekter ved matematikklæreres profesjonskunnskap. I denne artikkelen tar vi utgangspunkt i en av de mest anerkjente modellene, med tilhørende måleinstrument. Ball og kollegaer ved Universitetet i Michigan har utviklet en praksisbasert teori for å beskrive den sammensatte kunnskapen lærere trenger for å undervise i matematikk (Ball, Thames, & Phelps, 2008), og forskerne i Michigan-miljøet har også utviklet tester med flervalgsoppgaver for å måle og studere denne kunnskapen (Hill, Sleep, Lewis & Ball, 2007). På norsk omtales både teorien og måleinstrumentet ofte som undervisningskunnskap i matematikk – forkortet UKM (se Fauskanger, Bjuland, & Mosvold, 2010). Omfattende studier indikerer at UKM-instrumentet fungerer godt for å identifisere lærere som har god kvalitet på undervisningen (Hill, Umland, Litke, & Kapitula, 2012), og det ser også ut til å være en sammenheng mellom lærernes UKM-skår og elevenes prestasjoner i matematikk (Hill, Rowan, & Ball, 2005). En norsk oversettelse og tilpasning av UKM-instrumentet ser ut til å fungere bra (Fauskanger, Jakobsen, Mosvold, & Bjuland, 2012), men videre studier har indikert at det ikke alltid er samsvar mellom lærernes svar på flervalgs-oppgavene og deres skriftlige refleksjoner (Fauskanger & Mosvold, 2012). Det ser heller ikke ut til å være en klar sammenheng mellom flervalgssvar og den UKM lærere viser i intervjuer (Fauskanger & Mosvold, i trykk-b). I denne artikkelen undersøker vi sammenhengen mellom lærernes flervalgssvar og skriftlige svar på åpne oppgaver nærmere. Vår hypotese er at de utfordringene som ser ut til å være med ulike oppgaveformat kan henge sammen med hvilke aspekter ved lærernes kunnskap instrumentet måler. Vi går her inn i en kritisk diskusjon omkring utfordringene ved måling av ulike aspekter ved matematikklæreres kunnskap når vi tilnærmer oss følgende forskningsspørsmål:

Hvilket samsvar er det mellom de svarene matematikklærere gir på oppgaver med ulikt oppgaveformat?

For å svare på dette spørsmålet, har en gruppe norske lærere svart på et sett flervalgsoppgaver utviklet av Ball og kollegaer (vi refererer til disse som UKM-oppgaver) og åpne oppgaver som vi har utviklet i tilknytning til UKM- oppgavene (se f.eks., Fauskanger & Mosvold, i trykk-c). Ved hjelp av innholdsanalyse har vi sammenlignet lærernes flervalgssvar og deres svar på åpne oppgaver.

Måling av læreres kunnskap

Læreres kunnskap har stor betydning for elevers læring; det er en ”sannhet” som både politikere, forskere og andre ser ut til å være enige om. Videre ser det ut til å være enighet om at noen typer kunnskap er viktigere enn andre. Innenfor det matematikkdidaktiske fagfeltet peker forskningen i retning av en bestemt type kunnskap som er spesielt knyttet til undervisningen av faget. Denne tenkingen finner vi for eksempel i den tyske COACTIV-studien³, hvor en skiller mellom fagkunnskap (”content knowledge”) og fagdidaktisk kunnskap (”pedagogical content knowledge”) (Baumert et al., 2010). I COACTIV-studien ble det utviklet tester av fagkunnskap og fagdidaktiske kunnskap for lærere i videregående skole. Disse testene – som stort sett besto av åpne oppgaver – ble spesifikt utviklet for tyske forhold, men resultatene gir interessante indikasjoner på at særlig lærernes fagdidaktiske kunnskap hadde positiv påvirkning på elevenes resultater.

Både COACTIV-studien og de amerikanske studiene til Ball og kollegaer bygger videre på Shulmans teorier om lærerkunnskap, men det er likevel en del ulikheter mellom dem. Mens Baumert og kollegaer kun skilte mellom fag-kunnskap og fagdidaktisk kunnskap utviklet Ball og kollegaer (2008) et ramme-verk som inkluderte en videre oppdeling av disse to kategoriene av lærer-kunnskap (se figur 1). Analyser viser også at de tyske og amerikanske forskerne har kategorisert de ulike aspektene ved undervisningskunnskap i matematikk ulikt (Kaarstein, 2014). Mangelen på samsvar mellom definisjoner og kategorier av den matematiske kunnskapen lærere trenger for undervisning er en stor utfordring for forskningen.

En annen forskjell ligger i utbredelse. Mens COACTIV stort sett har blitt brukt i Tyskland, har instrumentet som ble utviklet av Ball og kollegaer blitt brukt i en rekke land over hele verden. Videre ble instrumentet i COACTIV-studien utviklet spesielt med tanke på matematikklærere i videregående skole, mens Ball og kollegaer hadde særlig fokus på lærere i grunnskolen. Med bakgrunn i dette fant vi det naturlig å bruke UKM-instrumentet som utgangspunkt i våre studier.

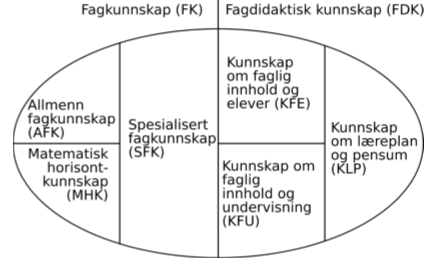
Selv om de ser på UKM som sammensatt av ulike typer kunnskap, fokuserer Ball og kollegaer særlig på det de kaller for spesialisert fagkunnskap i matematikk. Mens allmenn fagkunnskap er den matematiske kunnskapen en kan forvente at alle velutdannede voksne har, så er spesialisert fagkunnskap en type matematisk kunnskap som er spesielt knyttet til matematikkundervisning og som innebærer en dyp relasjonsforståelse av det faglige innholdet (Skemp, 1976). 

Testene i COACTIV-studien består stort sett av åpne oppgaver, mens forskerne i Michigan utviklet et instrument som utelukkende består av flervalgsoppgaver. Bruk av flervalgsformatet har sine fordeler. Et eksempel er at det er mindre tidkrevende å analysere flervalgssvar enn svar på åpne oppgaver. Flervalgsoppgaver er dermed velegnet for bruk i stor skala. Det er derimot ikke bare fordeler, og en ulempe ved bruk av flervalgsoppgaver er at de kan ha et for sterkt fokus på fakta- og prosedyrekunnskap (Haladyna, 2004). Buchholtz og kollegaer (2013) argumenterer for at flervalgsoppgaver ikke egner seg til å fange dybden av læreres UKM, og Schoenfeld (2007) la frem liknende argumenter i sin kritikk av UKM-oppgavene. Han foreslår at en bør investere ressurser i å utvikle åpne oppgaver og argumenterte videre for at det er mye arbeid som gjenstår for å undersøke hva slags lærerkunnskap det er relevant å måle og hvor velegnet UKM-oppgavene er i denne sammenheng.

Undervisningskunnskap i matematikk og forståelse

Allerede på 1970-tallet pekte Richard Skemp på betydningen av en dypere forståelse for matematiske sammenhenger (relasjonsforståelse) i forhold til en mer overfladisk prosedyrekunnskap – ofte kalt instrumentell forståelse (Skemp, 1976). Nyere forskning bekrefter dette, og viser at læreres relasjonsforståelse gjør at elever lærer mer matematikk enn om læreren har instrumentell forståelse (Tchoshanov, 2011). Disse ulike typene forståelse kan også knyttes til kunnskapskategoriene i UKM-modellen. Med UKM-oppgavene presentert i figur 2 som eksempel, vil vi synliggjøre noe av denne sammenhengen.

”Testlet” blir brukt på UKM-oppgaver sammensatt av flere flervalgsoppgaver som i figur 2. Dette testletet er utviklet for å måle spesialisert fagkunnskap. Det å multiplisere to tosifrede tall som 35 og 25 er noe alle utdannede voksne bør kunne; det er et eksempel på allmenn fagkunnskap. Det er fullt mulig å multiplisere 35 og 25 utelukkende ved hjelp av instrumentell forståelse der en kun anvender en prosedyre. Allmenn fagkunnskap inkluderer kunnskap om tallfakta og algoritmer – som Skemp (1976) kaller instrumentell forståelse. Vi kan likevel ikke sette likhetstegn mellom instrumentell forståelse og allmenn fagkunnskap. Allmenn fagkunnskap kan også inkludere dypere kunnskap om begreper og matematiske sammenhenger (det vil si relasjonsforståelse). Multiplikasjon av 35 og 25 kan altså innenfor rammen av allmenn fagkunnskap utføres instrumentelt. Det vil si at en person vet at en gitt algoritme gir korrekt produkt, men vedkommende vet ikke hvorfor algoritmen fungerer. En med god allmenn fagkunnskap kan selvfølgelig også ha dypere forståelse for hvorfor en gitt algoritme for tosifret multiplikasjon gir riktig produkt.

Oppgaven i figur 2 er derimot ikke bare ment å skulle måle allmenn fagkunnskap. For å svare på de tre flervalgsoppgavene kreves en dypere forståelse for hva som ligger til grunn for ulike algoritmer for å gjennomføre flersifret multiplikasjon. Dette er et eksempel på en matematisk kunnskap som er spesifikt knyttet til matematikklærerprofesjonen, og vi kaller dette for spesialisert fagkunnskap i matematikk. Denne oppgaven er utviklet for å måle læreres forståelse for hvorfor ulike algoritmer fungerer, og dette er et eksempel på spesialisert fagkunnskap som er knyttet til undervisningsarbeidet i mate-matikk (Ball et el., 2008). En som har spesialisert fagkunnskap vil kunne avgjøre hvorvidt ulike algoritmer kan benyttes til å finne produktet for alle hele tall (figur 2). Dette aspektet av læreres UKM inkluderer blant annet å vite hvorfor – ikke kun hvordan – og er nært relatert til Skemps (1976) relasjons-forståelse.

Siden læreres relasjonsforståelse er en viktig indikator på undervisning av høy kvalitet og for elevers læring (Tchoshanov, 2011), vil det være en forutsetning for kartlegging av lærerkunnskap at verktøyet som tas i bruk måler relasjonsforståelse.

Metodologisk tilnærming

Studien er del av en større studie (f.eks., Fauskanger & Mosvold, i trykk-a) og har et flermetodisk design (f.eks., Tashakkori & Creswell, 2007). For å studere sammenhengen mellom svarene lærere gir på flervalgsoppgaver og korresponderende åpne oppgaver – begge deler skriftlig – valgte vi å rekruttere lærere med kunnskap om norsk skolekontekst (eksempelvis læreplan og læremidler). Deltakerne i studien var matematikklærere med erfaring fra ulike trinn i grunnskolen. Det var en forutsetning at deltakerne hadde tid og lyst til å gå i dybden på oppgavene. Deltakere på et videreutdanningskurs i matematikk/matematikkdidaktikk (30 studiepoeng over tre semester) ble invitert til å delta, og datamaterialet ble produsert som en del av denne videreutdanningen. Av de 30 lærerne som deltok i studien var det 8 menn og 22 kvinner. Disse lærerne underviste på ulike trinn og hadde ulik erfaring og utdanning; 15 av lærerne arbeidet på småskoletrinnet, 10 på mellomtrinnet og 5 på ungdomstrinnet.

Instrumentet besto av 28 UKM-oppgaver som var oversatt og tilpasset for bruk i den norske konteksten (Fauskanger, et al., 2012; Mosvold, Fauskanger, Jakobsen & Melhus, 2009). Alle oppgavene ble opprinnelig utviklet av forskere ved Universitetet i Michigan. Bakgrunnen for valg av oppgaver var at de ifølge gjeldende læreplan for grunnskolen representerte relevant fagstoff for lærerne, og vi kan dermed understreke betydningen av at lærerne bør ha relasjonsforståelse (Skemp, 1976) relatert til dette fagstoffet.

For å studere sammenhengen mellom lærernes flervalgssvar og deres skriftlige refleksjoner, utviklet en gruppe forskere åpne spørsmål med utgangspunkt i UKM-oppgavene. De åpne spørsmålene ble utviklet i relasjon til det faglige innholdet i UKM-oppgavene og varierte følgelig noe fra oppgave til oppgave. Oppgavene ble også utviklet med den hensikt å studere type kunnskap vektlagt av den enkelte lærer. Følgende åpne spørsmål ble stilt til flervalgsoppgavene i figur 2:

1. Hva kan elevene når de svarer som elevene A, B og C over?
2. Hva, hvis noe, trenger elevene å lære mer om? (Hvorfor?)
3. Speiler oppgaven viktig matematikkfaglig/matematikkdidaktisk innhold på det trinnet du underviser? (Hvorfor?/Hvorfor ikke? Gi et eksempel fra klasserommet for å illustrere.)
4. Ville du anbefalt elevene dine å bruke noen av metodene som elevene A, B og C bruker? (Hvorfor?/Hvorfor ikke?)

De skriftlige refleksjonene ble gitt for hele testletet og ikke for hvert flervalgsspørsmål (som a), b) og c) i figur 2). Lærerne ble også utfordret til å skrive refleksjoner relatert til hvilken type kunnskap de fant viktig for å undervise i matematikk, samt hvorfor de fant denne typen kunnskap spesielt viktig. Videre ble de bedt om å skrive begrunnede refleksjoner omkring hvilke av de 28 UKM-oppgavene som representerte viktig lærerkunnskap og hvilke som ikke gjorde det. Tidligere analyser av læreres skriftlige refleksjoner indikerer at spørsmålene som ble stilt som utgangspunkt for de skriftlige refleksjonene egner seg til å studere forholdet mellom læreres flervalgssvar og skriftlige refleksjoner (Fauskanger & Mosvold, 2012). Disse innledende analysene danner et viktig utgangspunkt for valideringen av de åpne spørsmålene brukt i denne konteksten.

Analytisk enhet i denne studien var individuelle læreres respons på flervalgsoppgaver og deres skriftlige refleksjoner. For å studere sammenhengen mellom disse formene for respons, ble de skriftlige refleksjonene analysert gjennom kvalitativ innholdsanalyse (se f.eks., Fauskanger & Mosvold, 2014). Denne tilnærmingen ses på som både en fleksibel og systematisk tilnærming for å klassifisere og identifisere temaer eller mønstre i tekstdata (Hsieh & Shannon, 2005). Skemps (1976) arbeider danner utgangspunkt for den teoridrevne innholdsanalysen – eller den deduktive bruken av kategorier i fokus.

Tekstutsnitt fra lærernes skriftlige refleksjoner som indikerte fakta- og prosedyrekunnskap, eller andre aspekter som kunne knyttes til instrumentell forståelse, ble kodet som instrumentell forståelse. Tekstutsnitt som reflekterte forståelse for begreper og sammenhengen mellom dem, ulike løsninger på matematiske problemer, eller andre aspekter knytter til relasjonsforståelse, ble kodet som relasjonsforståelse. Relatert til flervalgsoppgavene i figur 2, ble tekstutdrag som eksempelvis vektla ulike strategier for å finne løsning på et problem som inkluderer flersifret multiplikasjon kodet som relasjonsforståelse, mens tekstutsnitt som vektla en bestemt standard algoritme for flersifret multiplikasjon ble kodet som instrumentell forståelse.

Resultater

For å for å undersøke graden av samsvar mellom læreres undervisningskunnskap i matematikk slik den måles ved henholdsvis flervalgssvar og skriftlige refleksjoner, vil vi i det følgende starte med å presentere resultatene fra analyser av lærernes flervalgssvar og deres skriftlige refleksjoner totalt sett. Deretter diskuterer vi resultatene fra en utvalgt oppgave (figur 2) som illustrasjon. Vi fokuserer her særlig på analyser av de skriftlige refleksjonene der det ikke er samsvar.

Tabell 1. Antall lærere med skriftlige refleksjoner (SR) som støtter opp under/ikke støtter opp under deres flervalgssvar (F)

	Overensstemmelse mellom flervalgssvar (F) og skriftlige refleksjoner (SR)		Manglende overensstemmelse mellom flervalgssvar (F) og skriftlige refleksjoner (SR)
Oppgave-nummer*	Riktig F og SR som indikerer relasjonsforståelse	Feil F og SR som indikerer manglende eller instrumentell forståelse	Riktig F og SR som indikerer manglende eller instrumentell forståelse	Feil F og SR som indikerer relasjons-forståelse
1	7	9	13	1
2	25	2	1	2
3	14	2	14	0
4	13	3	13	1
5	17	4	6	3
6	11	8	9	2
7	14	4	9	3
8	5	9	3	13
9	5	8	4	13
10	16	0	14	0

*Flervalgsspørsmålene inkludert i et testlet (figur 2) er i denne tabellen slått sammen til en celle – derfor blir det kun 10 oppgavenummer (1. kolonne)

En analyse av lærernes flervalgssvar alene viser at alle lærerne svarte riktig på 7 av de 28 oppgavene. For de resterende 21 oppgavene identifiserte mellom 8 og 29 lærere det riktige svaret i flervalgsoppgaven. Når lærernes flervalgssvar ses i sammenheng med deres skriftlige refleksjoner kan det se ut som om de bruker ulik type kunnskap som bakgrunn for sin flervalgssvar. Den type kunnskap lærerne har, kommer altså ikke nødvendigvis til uttrykk gjennom det flervalgssvaret de avgir. I de 28 inkluderte oppgavene viste opp til 13 lærere relasjonsforståelse i sine skriftlige refleksjoner – til tross for at de valgte feil flervalgssvar.

Da de inkluderte oppgavene har ulikt faglig innhold, og på grunn av den grundige analysen som kreves (Hsieh & Shannon, 2005), vil oppgavene presentert i figur 2 brukes som case for å illustrere resultatene. Disse oppgavene (nr. 6 i vårt oppgavesett) var utviklet for å måle læreres spesialiserte fagkunnskap, og dermed deres relasjonsforståelse. I utgangspunktet forventet vi at de erfarne lærerne i denne studien hadde relasjonsforståelse tilknyttet flersifret multiplikasjon. Når vi undersøkte forholdet mellom lærernes flervalgssvar til UKM-oppgavene (i figur 2) og de korresponderende skriftlige refleksjonene, var imidlertid ikke sammenhengen alltid rett frem (gruppe 1b og 2a, tabell 2). Interessant nok viste de øvrige tre oppgavene som var utviklet for å måle spesialisert fagkunnskap (oppgave 3, 8 og 9) også stor grad av manglende samsvar mellom flervalgssvar og skriftlige refleksjoner. Faktisk var det enda flere lærere som viste manglende samsvar mellom flervalgssvar og skriftlige refleksjoner i de tre andre oppgavene som målte spesialisert fagkunnskap

Tabell 2. Læreres flervalgssvar og skriftlige refleksjoner tilknyttet tosifret multiplikasjon (figur 2)

	Relasjonsforståelse	Mangel på/ instrumentell forståelse
Alle riktig (a)	11 lærere (gruppe 1a)	9 lærere (gruppe 2a)
En eller flere feil (b)	2 lærere (gruppe 1b)	8 lærere (gruppe 2b)

To av lærerne (gruppe 1b) ga feil svar på flervalgsoppgavene i oppgave 6 (figur 2), men deres skriftlige refleksjoner indikerte relasjonsforståelse for tosifret multiplikasjon. Disse to lærerne synes å vektlegge elevers utvikling av ulike algoritmer tilpasset oppgavetype og egne preferanser (Hatano, 2003). Dette kan tolkes som relasjonsforståelse som er viktig for å undervise i dette emnet (Even & Tirosh, 2002; Verschaffel, Greer & De Corte, 2007). En annen gruppe lærere (gruppe 2a) krysset av for riktig svar i flervalgsoppgavene, men analysen av deres skriftlige refleksjoner indikerte manglende forståelse, eller instrumentell forståelse. Siden disse flervalgsoppgavene var ment å skulle måle spesialisert fagkunnskap hvor relasjonsforståelse er viktig, valgte vi her å slå sammen manglende forståelse og instrumentell forståelse. Noen av de ni lærerne i gruppe 2a synes å være usikre på oppgavenes faglige innhold, og viser gjennom det de skriver at de mener at en bestemt algoritme for tosifret multiplikasjon alltid er best. For de resterende lærerne – det vil si de 11 i gruppe 1a og de 8 i gruppe 2b – var det sammenheng mellom flervalgssvar og skriftlige refleksjoner. Lærerne i gruppe 1a identifiserte de tre nøklene i flervalgsoppgavene og viste gjennom sine skriftlige refleksjoner relasjonsforståelse tilknyttet tosifret multiplikasjon. Lærerne i gruppe 2b skrev at de ikke forstår de presenterte algoritmene, eller viser at de har et instrumentelt syn på tosifret multiplikasjon. Dette er i tråd med det en ville forvente, at de som svarer feil ikke forstår, eller har overfladisk forståelse, mens de som svarer riktig har en dypere relasjonsforståelse.

Manglende samsvar

I det følgende vil vi presentere og diskutere resultatene mer i detalj, men med et spesielt fokus på de lærerne som hadde skriftlige refleksjoner som ikke støttet opp under deres flervalgssvar, det vil si lærerne i gruppe 1b og 2a (tabell 2).

Ti av de 30 lærerne krysset ikke av for det riktige svaret til en, to eller tre av flervalgsoppgavene inkludert i oppgaven i figur 2. Av de 20 lærerne som identifiserte det riktige svaret i alle tre flervalgsoppgavene, hadde ni av dem skriftlige refleksjoner som ikke støttet opp under avgitt flervalgssvar. Et eksempel er Inga (pseudonym). Hun identifiserte alle tre riktige flervalgssvarene – og dermed produktet i alle tre algoritmene – som korrekt, men hun skrev eksplisitt at hun ikke forstod de tre algoritmene elevene har brukt. De andre åtte lærerne, som hadde skriftlige refleksjoner som ikke støttet opp under deres flervalgssvar, fremhevet at elevene burde utvikle en bestemt standardalgoritme til fordel for adaptiv ekspertise (Hatano, 2003). En av disse lærerne, Brit, skrev: ”De [elevene] trenger å jobbe seg frem til en standard algoritme. Ellers vil de bruke mye tid på store tall og lange ramser med addisjon”. Brit vektlegger tempo, heller enn forståelse i sine skriftlige refleksjoner. De andre ni lærerne i denne gruppen indikerer at de, før elevene er klar for det, vil vektlegge undervisning av standardalgoritmer (Verschaffel, et al., 2007). Frida er et annet eksempel, hun skriver blant annet at elevene som regner som i figur 2

trenger å lære den måten som læres i den norske skolen. En metode som jeg synes er et enklere oppsett. Det elevene må lære seg da er tieroverganger og tallenes plassering (posisjonssystemet), og etter hvilken retning vi begynner utregningen.

Hun viser så til en konkret algoritme som er nesten identisk med den elev B har brukt. Den eneste forskjellen er at hun skrev 700 som 70 tiere i sin utregning. Frida knytter ikke sin anbefalte algoritme til elev B sin algoritme, men fremhever sitt forslag som enklere og bedre enn de tre elevene A, B og C bruker.

Det var to lærere som ikke identifiserte alle tre nøklene, men som gjennom sine skriftlige refleksjoner viste at de hadde dyp forståelse for flersifret multiplikasjon (gruppe 1b i tabell 2). I det følgende ser vi nærmere på disse to lærernes skriftlige refleksjoner. Ragna svarte ”Jeg er ikke sikker” (kodet som feil) på to av oppgavene i figur 2. Likevel fremhever hun i sine skriftlige refleksjoner nødvendigheten av at undervisningen legger til rette for at elever utvikler forståelse for ulike algoritmer, eller adaptiv ekspertise (Hatano, 2003) – at elevene støttes i denne prosessen. Ragna skriver at elevene A, B og C kanskje trenger ”å lære den norske måten å multiplisere flersifrede tall på, fordi de da kan få en forståelse av at det være andre måter å løse en multiplikasjonsoppgave på”. Hun fremhever videre at norske elever på samme måte kan ”få kjennskap til at

det er flere måter en kan løse en multiplikasjonsoppgave på”, men at det er viktig å prøve å se hvilken metode elevene bruker for å komme fram til svaret på i oppgaver, fordi en da eventuelt kan hjelpe dem videre og elevene får bekreftelse på eget arbeid. Dette kan òg være viktig i forhold til nye elever som begynner i klassen som kommer fra andre land og de kan ha lært andre strategier for å løse oppgaver enn det som kan være vanlig her i Norge.

Den andre læreren, Oda, svarte at elevene A og B (figur 2) bruker algoritmer som ikke kan brukes til å multiplisere to vilkårlige hele tall. Fra hennes skriftlige refleksjoner er det imidlertid klart at hun har relasjonsforståelse (Skemp, 1976) tilknyttet tosifret multiplikasjon. Hun skriver en stegvis og detaljert beskrivelse av hva elevene som bruker de tre ulike algoritmene har gjort. Årsaken til at Oda ga uriktig flervalgssvar tilknyttet a) og b) ser – ut fra hennes skriftlige refleksjoner – ut til å være hennes tolkning av ”vil fungere”. Som en kan se av figur 2, inviterer flervalgsoppgavene lærerne til å finne ut hvilke av metodene A, B og C som ”vil fungere” og ”ikke vil fungere” når en skal multiplisere to vilkårlige hele tall. Det å ”ikke fungere” kan tolkes ulikt, og Oda ser ut til å relatere dette til at metodene blir tungvinte om tallene har flere sifre enn to. Oda skriver at hun vil veilede elevene mot en algoritme som ikke er så tidkrevende og som kan brukes mer effektivt, men hun understreker nødvendigheten av at elevers flersifrede regning og de algoritmer de bruker må baseres på elevenes relasjonsforståelse (Skemp, 1976). Hun skriver at en algoritme for tosifret multiplikasjon må baseres på forståelse for distributive, assosiative og kommutative egenskaper ved multiplikasjon. Odas skriftlige refleksjoner indikerer at hun vil unngå prematur undervisning av standardalgoritmer (Verschaffel, et al., 2007).

Avsluttende diskusjon

I denne studien har vi fokusert på sammenhengen mellom svarene lærere gir på spørsmål av ulike format. Vi har tatt utgangspunkt i de amerikanske flervalgsoppgavene utviklet for å måle undervisningskunnskap i matematikk, og så har vi lagt til mer åpne spørsmål knyttet til innholdet i disse. Mens UKM-oppgavene måler lærernes kunnskap, har vi altså brukt lærernes skriftlige svar på de åpne oppgavene for å finne ut mer om lærernes forståelse. Eksempeloppgaven i figur 1 er utviklet for å måle læreres spesialiserte fagkunnskap i matematikk, og dette er en type kunnskap som er nært relatert til relasjonsforståelse. I resultatene fra studien vår ser vi at de fleste lærerne som indikerer relasjonsforståelse også svarer riktig på UKM-oppgavene, og motsatt ser vi at lærerne som indikerer manglende forståelse svarer feil på en eller flere av de tilhørende UKM-oppgavene. Samtidig ser vi at det er en del lærere som ikke viser relasjonsforståelse, men som likevel svarer riktig på UKM-oppgavene, og motsatt ser vi også at to av lærerne som viser god relasjonsforståelse svarer feil på UKM-oppgavene. Her ser vi noen likhetstrekk med funnene til Hill og kollegaer (2012). Da de undersøkte sammenhengen mellom amerikanske læreres svar på UKM-oppgaver og kvaliteten på undervisningen, fant de ut at det var en del lærere med svak undervisningskvalitet som likevel hadde høy UKM-skår. I vår studie finner vi en lignende tendens når en del lærere som ikke viser relasjonsforståelse i svarene på de åpne oppgavene likevel svarer riktig på UKM-oppgavene. Hill og kollegaer fant også at enkelte lærere med svært god undervisningskvalitet likevel hadde relativt lav UKM-skår, og i vår studie finner vi også at et par lærere med god relasjonsforståelse likevel svarer feil på UKM-oppgavene. Det er altså ikke alltid en klar sammenheng mellom lærernes svar på flervalgsoppgavene og de mer åpne oppgavene. Denne mangelen på samsvar ble funnet i nesten alle oppgavene i studien vår.

På den ene siden kan resultatene fra studien vår ses på som en kritikk av kvaliteten på UKM-oppgavene oversatt og tilpasset den norske konteksten. Samtidig er dette et instrument som er grundig utviklet og testet ut på store mengder lærere – både i USA og mange andre land – og som viser seg å fungere godt. Dermed kan kanskje resultatet heller tolkes som en støtte for hypotesen om at ulike format måler ulike typer kunnskap. Det å legge til åpne oppgaver hvor lærerne kan komme med skriftlige refleksjoner gir ikke automatisk en bedre innsikt i læreres kunnskap. På samme måte får en ikke nødvendigvis får bedre forståelse av læreres kunnskap ved å legge til undersøkelser av undervisningskvaliteten (jf. Hill et al., 2012). Slike utvidelser gjør det mer komplekst. På den andre siden viser resultatene av studien vår at selv om UKM-oppgavene ser ut til å fungere godt, så er det noen utfordringer. En kan risikere at enkelte lærere med god relasjonsforståelse ikke blir identifisert gjennom resultatene av UKM-oppgavene, og en kan også risikere at en del lærere som har svak relasjonsforståelse likevel kan få relativt god UKM-skår.

Det er flere mulige forklaringer til funnene i våre studier, og en mulighet er at resultatene har å gjøre med kulturelle hindringer knyttet til norske læreres møte med flervalgsformatet (Fauskanger, Mosvold, Bjuland & Jakobsen, 2011). En annen mulighet er at det handler om kulturelle forskjeller knyttet til forståelsen av det faglige innholdet i de konkrete oppgavene (Fauskanger & Mosvold, 2013). Andre forklaringer er også mulige, men vi ønsker her særlig å understreke at læreres skår på en flervalgsoppgave – eller en åpen oppgave – må brukes med forsiktighet. Utfordringene med å studere læreres kunnskap er fremtredende i begge format, og sammenhengene er komplekse. For videre forskning vil det kunne være relevant å undersøke om en finner lignende sammenhenger mellom læreres svar på flervalgsoppgaver og åpne oppgaver i andre land eller i et større utvalg av norske lærere. En fruktbar tilnærming kan også være å rekontekstualisere UKM-oppgavene til scenarier som kan brukes i kvalitative studier av aspekter av læreres UKM slik som Adler og Patahuddin (2012) har gjort. Disse forskerne argumenterer for at de gode UKM-oppgavene fremprovoserer læreres matematiske resonnering tilknyttet slike scenarier. Til sist kan det være interessant å følge opp disse studiene av sammenhengen mellom lærernes svar på oppgaver med ulike format og deres undervisningskvalitet (jf. Hill et al., 2012).

Dersom en skal måle og studere kunnskapene til norske matematikklærere, er det viktig å ha et kritisk blikk på hvilken kunnskap som skal måles, hvordan denne kunnskapen eventuelt skal måles, og ikke minst hvorfor. Sjøberg (2014) og andre advarer mot feil bruk av resultater fra PISA-studien, og på samme måte vil vi rette en sterk advarsel mot feil bruk av resultater fra måling av matematikklæreres kunnskap. UKM-instrumentet ble utviklet av forskerne ved Universitetet i Michigan for å lære mer om hvordan læreres undervisnings-kunnskap i matematikk er sammensatt og hvilken betydning den har. Dette instrumentet ble ikke utviklet for å måle enkeltlæreres kunnskap eller rangere lærere. Dersom regjeringens planer om kartlegging av matematikklærere og nasjonale prøver i matematikk for norske grunnskolelærerstudenter skal settes ut i livet, så vil både politikere, didaktikere og utdanningsforskere ha en utfordrende oppgave foran seg. Det vil være utfordrende å avgjøre hvilke instrumenter en vil ta i bruk, hvordan resultatene skal analyseres, og ikke minst hvordan resultatene skal tolkes og brukes. Denne studien har vist at det ikke alltid er samsvar mellom læreres svar på oppgaver av ulike oppgaveformat, og dette gir en indikasjon på noen av utfordringene som er involvert.