Profesjonskunnskap for matematikklærerutdannere

Matematikklærerutdannere skal utdanne lærere som har solid og reflektert kunnskap om undervisning i matematikk for de trinn de skal undervise på. De amerikanske forskerne Deborah L. Ball og Hyman Bass (2003) innførte begrepet mathematical knowledge for teaching som et overordnet begrep for å beskrive hvilken kunnskap en lærer trenger for å undervise i matematikk. Vi vil referere til dette begrepet som undervisningskunnskap i matematikk (UKM). Med utgangspunkt i beskrivelsen av UKM drøfter vi hvilken kunnskap en matematikklærerutdanner i grunnskolelærerutdanning trenger for å kunne legge til rette for at lærerstudenter utvikler UKM.

Undervisningskunnskap i matematikk

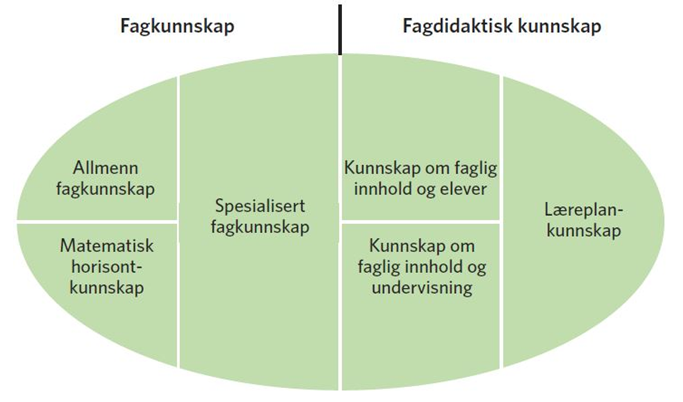
Hvilken kunnskap i matematikk er det en matematikklærer bør kunne, men som en matematiker eller en lærer i et annet fag ikke trenger å kunne? Shulman (1986) identifiserer to hovedkategorier av kunnskap, fagkunnskap og fagdidaktisk kunnskap, og fremhever at de er tett koblet. Shulmans arbeid danner utgangspunkt for flere undersøkelser der Ball og hennes medarbeidere har vært sentrale (se f.eks. Ball og Bass, 2003; Ball, Thames og Phelps, 2008).

Ball, Thames og Phelps (2008) analyserer hva arbeidet til en matematikklærer går ut på og hva slags kunnskap som trengs til de ulike oppgavene, og de identifiserer seks hovedelementer av undervisningskunnskap i matematikk, som vist i Figur 1:

Allmenn fagkunnskap defineres som matematikkunnskap som brukes ikke bare av lærere, men også av andre som arbeider med matematikk. Det innebærer blant annet å kunne løse et matematisk problem, avgjøre om et elevsvar et riktig eller feil, om notasjonen som eleven eller læreboka bruker er riktig, om eleven bruker et begrep, en definisjon eller en fremgangsmåte riktig.

Spesialisert fagkunnskap er matematikkunnskap som er spesiell for matematikklærere og som ikke er nødvendig for andre enn dem. Det er en viktig oppgave for en lærer å «pakke ut» det faglige innholdet slik at det blir tilgjengelig for elevene. Det innebærer blant annet å kunne identifisere viktige matematiske ideer og muligheter som en oppgave kan inneholde. Den spesialiserte fagkompetansen består også i å være bevisst ulike måter å fremstille en matematisk operasjon eller idé på. I tillegg er fordeler og ulemper ved bruk av ulike representasjoner, forklaringer og argumentering en del av den spesialiserte fagkunnskapen.

Kunnskap om faglig innhold og elever defineres som lærerkunnskap om ulike måter elevene kan tenke på, hva de kan finne utfordrende, hvilke oppgaver som kan tenkes å virke interessante og motiverende og om en oppgave vil være lett eller vanskelig. Videre innebærer denne kunnskapen å kunne høre og tolke elevenes innspill og å ha kunnskap om vanlige forestillinger og misoppfatninger innenfor et gitt matematisk tema.

Kunnskap om faglig innhold og undervisning er matematikkunnskap som brukes i planlegging av undervisning. Denne kunnskapen kommer til syne i valget av eksempler og aktiviteter som legger til rette for utvikling av en dypere forståelse for det gitte matematiske innholdet, i vurderingen av fordeler og ulemper med en gitt oppgave eller fremgangsmåte, og i det å vite hvilke spørsmål som kan være produktive og fremme forståelse i arbeidet med et matematisk problem.

I tillegg til disse fire elementene identifiserer Ball et al. (2008) læreplankunnskap og horisontkunnskap som en del av undervisningskunnskapen i matematikk. Det er kunnskap om hvordan de matematiske emnene fra læreplanen er relatert og hvordan de utvikles videre i elevers utdanning. Kunnskapen matematikklærere trenger for å undervise i faget, har en matematisk og en matematikkdidaktisk side, men de er tett sammenflettet slik det er fremhevet i beskrivelsen av de ulike elementene. Det faglige innholdet, et gitt begrep, en fremgangsmåte, representasjon eller sammenheng, har avgjørende rolle for hvilken type spørsmål, oppgave eller arbeidsmåte som kan være hensiktsmessig i undervisningen.

Internasjonalt har beskrivelsen av matematikklærerkunnskapen gitt av Ball et al. (2008) hatt stor betydning for forskning og utvikling innenfor lærerutdanning, etterog videreutdanning av lærere og forskning på utvikling av matematikklærerkompetanse. I Norge tas det utgangspunkt i UKM i rammeplaner for matematikkemner i grunnskolelærerutdanning.

Lærerutdanneres undervisningskunnskap i matematikk

For å identifisere hvilken type kunnskap som det er ønskelig at en lærerutdanner i matematikk har, kan man stille tilsvarende spørsmål som ovenfor: Hva er det spesielle en matematikklærerutdanner bør kunne, men som en matematiker, en matematikklærer eller en lærerutdanner i et annet fag ikke trenger å kunne?

Med utgangspunkt i modellen for undervisningskunnskap for matematikklærere gitt av Ball et al. (2008) ovenfor og en analyse av undervisningsoppgaver til en matematikklærerutdanner, har vi identifisert seks hovedelementer av lærerutdanneres undervisningskunnskap i matematikk (LUKM), som skissert i Figur 2.

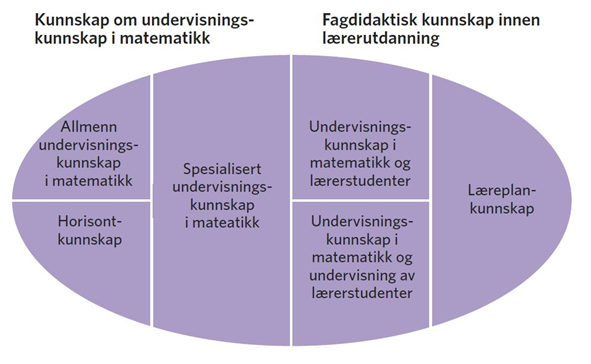
Lærerutdanneres undervisningskunnskap i matematikk kan, tilsvarende som i undervisningskunnskap til matematikklærere, betraktes som bestående av to hovedområder:

• fagkunnskap som er tett knyttet til det lærerutdannere skal undervise i, her er det kunnskap om undervisningskunnskap i matematikk
• fagdidaktisk kunnskap om læring og undervisning av det som skal læres/undervises, her er det fagdidaktisk kunnskap innen lærerutdanning

Mye matematikkdidaktisk teori og forskning er knyttet til elevers læring og matematikkundervisning i skolen, og denne delen er det vanlig å arbeide med i lærerutdanning. På en annen side er det et stadig voksende felt innen matematikkdidaktisk forskning som studerer lærerstudenters utvikling av undervisningskunnskap, og denne forskningen vil ha en betydning for lærerutdanneres arbeid med studenter. Nedenfor beskriver vi kort de ulike elementene innen hvert av områdene av LUKM og eksemplifiserer elementene ved å ta utgangspunkt i matematikkdidaktisk forskning. I arbeidet med lærerstudenter vil de ulike elementene være i tett samspill.

Allmenn undervisningskunnskap i matematikk – undervisningskunnskap i matematikk som brukes ikke bare av lærerutdannere, men også av matematikklærere. Lærerutdannere bør ha faglig og fagdidaktisk kunnskap som beskrevet i UKM-modellen til Ball et al. (2008). Det innebærer å ha dyp forståelse for matematiske begreper og sammenhenger som er relevante for undervisning på de gitte trinnene, og det innebærer videre å ha kjennskap til og forståelse for matematikkdidaktisk forskning om undervisning og læring av matematikk. Med andre ord, matematikklærerutdannere bør selv ha undervisningskunnskap i matematikk innenfor de gitte trinnene lærerstudentene utdannes til.

Horisontkunnskap innen lærerutdanneres undervisningskunnskap i matematikk innebærer kjennskap til hvordan undervisningskunnskap i matematikk kan utvikles videre, etter at studentene er ferdig utdannet som lærere. Ebby (2000) ser det å lære av egen praksis som er en forutsetning for videre utvikling som matematikklærer.

Hun argumenterer for at det må arbeides bevisst i lærerutdanningen med å hjelpe lærerstudenter til å utvikle en vane og evne til å lære fra egen undervisning. Profesjonelt fellesskap, faglige diskusjoner og samarbeid mellom matematikklærere ved en skole har en sentral rolle for livslang læring og utvikling av undervisningskunnskap. Et slikt fellesskap kan for eksempel ta utgangspunkt i læreres faglige diskusjoner omkring elevarbeid (se Kazemi og Franke, 2004).

Spesialisert undervisningskunnskap i matematikk er undervisningskunnskap i matematikk som er spesiell for matematikklærerutdannere, og som ikke er nødvendig å ha for andre enn dem (som f.eks. matematikklærere i andre skoleslag eller lærerutdannere innen andre fag). Denne kunnskapen innebærer blant annet å kunne identifisere viktige matematiske og matematikkdidaktiske ideer og muligheter som en case, praksisoppdrag eller annen type oppgave i lærerutdanning kan gi. Videre innebærer det å kunne identifisere kritiske aspekter ved undervisningskunnskap i matematikk, kunne utforme aktiviteter og spørsmål som «pakker dem ut» og gjør dem tilgjengelige for lærerstudenter.

Et eksempel på et kritisk aspekt har vi i forskningen til Hill, Rowan og Ball (2005), som viser hvordan matematisk kunnskap har en helt sentral rolle for å kunne legge til rette for elevers læring. I arbeidet med lærerstudenter innebærer det et behov for å få frem det matematikkfaglige innholdet for eksempel i en case det arbeides med, og fremheve hvilken rolle dette har for hvilke typer spørsmål som kan stilles for å fremme elevers tenking. For å kunne gjøre det, må lærerutdanneren ha en dyp forståelse av matematiske begreper og sammenhenger, kjennskap til fagets oppbygging og natur, egne erfaringer med matematisk arbeid på et høyere nivå enn det man underviser i, og forståelsen for matematisk tenking og arbeidsmåter.

I arbeidet med å tilrettelegge for studentenes utvikling av UKM trenger lærerutdanneren også matematikkdidaktisk kunnskap om elevers matematikklæring og kunnskap om matematikkundervisning utover det som vanligvis undervises i lærerutdanningen. Et eksempel er kunnskap om teori og forskning på betydningen ulike representasjoner (som tegninger, regnefortellinger, konkreter, tabeller, grafer, muntlig språk, matematiske symboler) har for matematisk arbeid og matematikklæring (se for eksempel Duval, 2006). Slik kunnskap kan bidra i utvikling av oppgaver og spørsmål som retter lærerstudentenes oppmerksomhet mot betydningen av ulike representasjoner i matematikk og utfordringer som kan oppstå.

Undervisningskunnskap i matematikk og lærerstudenter defineres som kunnskapen til matematikklærerutdannere om ulike måter lærerstudenter kan tenke på, hva de kan finne utfordrende, hvilke oppgaver som kan tenkes å virke interessante og motiverende og om en oppgave vil være lett eller vanskelig. Videre innebærer denne kunnskapen å kunne høre og tolke lærerstudentenes innspill og å ha kunnskap om vanlige forestillinger lærerstudenter kan ha om matematikk, matematikkundervisning og -læring.

Et eksempel på matematikkdidaktisk forskning innenfor dette elementet av LUKM er forskningen til Lo, Grant og Flowers (2008), som viser lærerstudenters ulike måter å argumentere på for ulike multiplikasjonsstrategier, type representasjoner de tar i bruk og typiske utfordringer studentene har. Et annet eksempel er studien til Nicol (1999) over utfordringer lærerstudenter har med å lære å stille spørsmål til elevene, lytte til deres innspill og gi tilbakemelding. Enge og Valenta (2010) påpeker i sin studie at lærerstudenter gjerne er svært opptatt av elevers læring og hvordan de kan legge til rette for den.

Samtidig overser lærerstudenter ofte betydningen av det matematiske innholdet i oppgaven elevene skal arbeide med og hvordan dette bør påvirke valg av arbeidsmåter og spørsmål som kan stilles for å fremme forståelse. Når analysen av oppgavens matematiske innhold mangler, blir lærerstudenters refleksjoner om egne praksisepisoder, elevers læring og egen undervisning nokså generelle og har lite potensial for å bidra til videre utvikling av undervisningskunnskapen i matematikk.

Undervisningskunnskap i matematikk og undervisning av lærerstudenter er kunnskapen til matematikklærerutdannere som tas i bruk i planlegging av undervisning av lærerstudenter. Denne kunnskapen kommer til syne i valg av eksempler og aktiviteter for å legge til rette for utvikling av undervisningskunnskap i matematikk, i vurdering av fordeler og ulemper ved en gitt aktivitet i undervisningen, og i det å vite hvilke spørsmål som det er essensielt å ta opp i diskusjon med lærerstudenter.

Måsøval (2011) undersøker lærerstudentenes arbeid med oppgaver innenfor algebraisk generalisering, og hun trekker spesielt frem rollen oppgavenes utforming har for studentenes mulighet for å utvikle den tilsiktede kunnskapen. Koblingen mellom teori og praksis er et aspekt som flere undersøkelser fremhever som viktig for utvikling av lærerstudentenes undervisningskunnskap i matematikk (se Empson og Jacobs, 2008; Zaslavsky, Chapman og Leikin, 2003). McDuffie, Drake og Herbel-Eisenmann (2008, s. 247) fremhever to kritiske momenter i utviklingen av UKM, momenter som er tett koblet sammen. Det ene er å lære didaktisk teori i praksissituasjoner der det er behov for slik teoretisk kunnskap.

Det andre momentet er utvikling av dyp matematisk forståelse, som er nødvendig for å undervise matematikk. Et viktig spørsmål i arbeid med lærerstudenter er da hvordan behovet for læring av didaktisk teori og utvikling av dyp matematisk forståelse kan fremmes i undervisning og i arbeid i praksis. I arbeidet med lærerstudenter legger Lampert m.fl. (2010) vekt på at man har aktiviteter som tar opp typiske hendelser fra praksis (som å lede en samtale med elever om et gitt regnestykke), aktiviteter der kompleksiteten i det å være matematikklærer bevares, men uten at man gjør det så komplisert at en lærerstudent ikke klarer å mestre dem. Slike aktiviteter kaller Grossmann, Hammerness og Mc Donald (2009, s. 280) for kjernepraksiser, og de argumenterer for bruk av slike aktiviteter i lærerutdanning (uavhengig av fag) for å styrke sammenheng mellom teori og praksis i utvikling av lærerkompetanse.

Læreplankunnskap innen lærerutdanneres undervisningskunnskap i matematikk innebærer kunnskap om og kompetanse til å utarbeide læreplaner i matematikk i lærerutdanning. I arbeidet med læreplaner er det viktig å ha forståelse for utdanningssystemet i Norge, verdier som skal fremheves gjennom lærerutdanningen og kunnskaper lærerstudenter skal utvikle for å kunne oppfylle sin lærerrolle.

I utarbeidelsen av læreplaner er det mange valg som må tas, og det er alltid nødvendig å prioritere noe fremfor noe annet. Kunnskap innen matematikkdidaktisk forskning, kjennskap til «den typiske» lærerstudentens faglige bakgrunn og studentens fremtidige oppgaver som lærer i utdanningssystemet, er viktig når valgene skal tas i arbeidet med læreplaner (se for eksempel Mc Duffie et al., 2008).

Implikasjoner

Det er ingen utdanning som utdanner matematikklærerutdannere. Som oftest har de som ansettes til å undervise matematikk i lærerutdanning i Norge, en mastergrad eller doktorgrad innen matematikk eller matematikkdidaktikk.

I tillegg er det et krav om at de har praktisk-pedagogisk utdanning eller undervisningserfaring fra grunn- eller videregående skole. For dem som har matematikkbakgrunn kan utvikling av profesjonskunnskap som matematikklærerutdanner være krevende, da det er mange aspekter som man ikke har møtt gjennom egen utdanning og yrkeserfaring. De som har matematikkdidaktisk utdanningsbakgrunn har en kjennskap til det didaktiske feltet og inngangen i lærerutdanning kan være enklere. Samtidig har de fleste av disse studert temaer knyttet til elevers læring og undervisning av matematikk i skolen. De har dermed heller ikke nødvendigvis kunnskap om lærerutdanning og lærerstudenter.

Matematikklærerutdannere utvikler gjerne sin kunnskap gradvis, gjennom undervisningserfaring og refleksjon, lesing, utviklingsarbeid og forskning. Kunnskapen som skal utvikles er kompleks, og veien kan være lang når man går den alene. Lærerutdanningene bør finne systematiske måter for å tilrettelegge utvikling av lærerutdanneres kompetanse, og slik hjelpe lærerutdannere i utviklingen av kunnskap og samtidig bidra til kvaliteten i lærerutdanningen.