Sentrale kjennetegn på god læring og undervisning i matematikk

Målet med denne artikkelen er å sette fokus på forskning om god læring og undervisning i matematikk ved å gi en sammenfattet og lett tilgjengelig - men samtidig faglig robust - oversikt over sentrale ideer innen dette forskningsfeltet. Vi vil referere til både norsk og internasjonal litteratur, men vil hele tiden å beholde den norske konteksten som bakgrunn for det som blir presentert.

Definisjoner av god læring og undervisning i matematikk kan variere over tid og vil være avhengig av sosiale, økonomiske og kulturelle forhold. I tillegg vil det vi anser som formålene med et utdanningssystem danne grunnlaget for potensielle anbefalinger om forbedringer. For å kunne beskrive kjennetegn på god undervisning og læring i matematikk, må vi først skissere målene som er forbundet med matematikkfaget.

I LK06 (Kunnskapsdepartementet, 2006) er følgende faktorer nevnt:

Matematikk er ein del av den globale kulturarven vår. Mennesket har til alle tider brukt og utvikla matematikk for å utforske universet, for å systematisere erfaringar og for å beskrive og forstå samanhengar i naturen og i samfunnet. Ei anna inspirasjonskjelde til utviklinga av faget har vore glede hos menneske over arbeid med matematikk i seg sjølv. Faget grip inn i mange vitale samfunnsområde, som medisin, økonomi, teknologi, kommunikasjon, energiforvalting og byggjeverksemd. Solid kompetanse i matematikk er dermed ein føresetnad for utvikling av samfunnet. Eit aktivt demokrati treng borgarar som kan setje seg inn i, forstå og kritisk vurdere kvantitativ informasjon, statistiske analysar og økonomiske prognosar. På den måten er matematisk kompetanse nødvendig for å forstå og kunne påverke prosessar i samfunnet.

... Matematikk ligg til grunn for viktige delar av kulturhistoria vår og for utviklinga av logisk tenking. På den måten spelar faget ei sentral rolle i den allmenne danninga ved å påverke identitet, tenkjemåte og sjølvforståing.

…Det må leggjast til rette for at både jenter og gutar får rike erfaringar som skaper positive haldningar og ein solid fagkompetanse. Slik blir det lagt eit grunnlag for livslang læring. 

Disse målene antyder at elever må lære å tenke, resonnere og løse problemer på en selvstendig måte og med selvinnsikt. Det finnes ingen absolutte regler for hvordan dette kan oppnås, men forskning har vist at vi bør bevege oss vekk fra ideen om at matematikk hovedsakelig består av regler og algoritmer som må læres utenat. Fokuset bør snarere rettes mot de rike tankeprosessene som underligger matematisk aktivitet, og flere større europeiske forsknings- og utviklingsprosjekter som Norge har tatt del i (f. eks. S-TEAM, PRIMAS, MaScil) har hatt som mål å fremme dette - blant annet gjennom undersøkende matematikkundervisning (inquiry based learning and teaching). 

I de neste seksjonene vil vi belyse fem temaer som har stått sentralt i matematikkdidaktisk forskning over lengre tid, og som vi ønsker å fremheve på det nåværende tidspunkt: 1) undersøkende matematikkundervisning, 2) forståelse, 3) selvinnsikt og bevissthet, 4) motivasjon og 5) tilpasset opplæring.

Vi vil ikke gå inn på spesifikke oppgaver eller klasseromsopplegg, men vil heller fokusere på generelle fremgangsmåter og holdninger til matematikkfaget, med en annerkjennelse om at slike holdninger kan omfavne en rekke varierte undervisningsopplegg.

Vi vil påpeke at denne rapporten presenterer en liten del av et forskningsfelt i rask utvikling. Allikevel ønsker vi, gjennom den valgte litteraturen, å rette fokuset på aspekter som vi betrakter som svært aktuelle og sentrale i matematikkopplæringen i Norge i dag. Selv om vi mener at påstandene vi presenterer om god læring og undervisning i matematikk er godt dokumentert i litteraturen, vil vi ikke presentere en fullstendig gjennomgang av forskningslitteraturen for å støtte dem. Vi vil i stedet velge ut bestemte teorier og studier for å illustrere våre påstander og henvise leseren til andre, mer utfyllende reviews av relevant forskning.

Undersøkende matematikkundervisning

Matematikklasserom i Norge følger ofte en tradisjonell, lærebokstyrt undervisningsform hvor læreren introduserer dagens tema, viser eksempler på tavlen og deretter ber elevene om å løse oppgavene som står i boken (Alseth, Breiteg, & Brekke, 2003). Det legges stor vekt på vise hvordan man finner det riktige svaret, og oppgavene elevene arbeider med er ofte like i strukturen (om ikke identiske). Å vite hvorfor og det å se sammenhenger får mindre oppmerksomhet.

En alternativ undervisningsform som det er forsket mye på - både i Norge og internasjonalt - er undersøkende matematikkundervisning (inquiry based teaching). En undersøkende matematikktime skiller seg i betydelig grad fra tradisjonell undervisning, og den følger ofte en tredelt struktur (Goos, 2004; Sherin, 2002). I begynnelsen av timen presenterer læreren en ny og kognitivt krevende oppgave eller aktivitet for elevene. Deretter får elevene god tid til å jobbe med denne aktiviteten. Læreren observerer arbeidet deres og kan oppmuntre dem til å finne nye løsninger eller til å beskrive hvordan de tenker. Timen avsluttes med at hele klassen diskuterer aktiviteten og de forskjellige løsningsmetodene som har blitt gjort. Læreren leder diskusjonen på en måte som gjør at elevene blir oppmerksomme på hvordan de ulike løsningene henger sammen og hvordan løsningene deres er relatert til læringsmålene for timen (Stein, Engle, Smith, & Hughes, 2008; Wæge, 2007; Smith & Stein, 2011). Elevene må både utvikle en forståelse for prosedyrene og de må kunne bruke prosedyrene effektivt, nøyaktig og fleksibelt.

Det bør også nevnes at undersøkende matematikkundervisning ofte (men ikke alltid) tar utgangspunkt i et konkret objekt som kan manipuleres og som visuelt og fysisk kan representere en rekke abstrakte matematiske ideer (Moyer, 2001). Bruk av slike ”konkreter” har blitt anbefalt i forskningslitteraturen (e.g. Raphael & Wahlstrom, 1989; Sowell, 1989; Tooke, Hyatt, Leigh, Snyder, & Borda, 1992), men det har også blitt påpekt at matematisk forståelse ikke simpelthen går gjennom fingertuppene og opp armen til en elev som jobber med objektet (Ball, 1992). For at bruk av konkreter skal ha en positiv effekt på læring må elevene reflektere over bruken av objektet og konstruere forståelse gjennom dette (Thompson, 1994; Moyer, 2001).

Forståelse

I diskusjonen om tradisjonelle og undersøkende undervisningsmetoder tas det i litteraturen ofte utgangspunkt i Skemps (1976) skille mellom instrumentell og relasjonell forståelse i matematikk, der instrumentell forståelse ofte knyttes opp mot tradisjonelle undervisningsformer, mens relasjonell forståelse gjerne forbindes med undersøkende fremgangsmåter til faget.

Instrumentell forståelse innebærer å lære et økende antall regler og formler som hjelper eleven med å finne løsningen på oppgavene; eleven vet hvordan oppgaven skal løses. Relasjonell forståelse innebærer å bygge opp begrepsmessige strukturer og se sammenhenger mellom begrepene. Det innebærer å vite både hvordan en oppgave skal løses og hvorfor det blir sånn. Skemp bruker følgende eksempel til å illustrere forskjellen på de to typene forståelse:

En person med en rekke bestemte instrukser kan finne veien fra et startpunkt til en rekke endepunkt. Instruksene forteller ham eller henne hva som må gjøres hver gang et valg må tas: Ta til høye ut døren, gå rett forbi kirken og så videre. Men hvis denne personen gjør en feil i forhold til instruksene på noe tidspunkt, så vil hun gå seg bort. Derimot vil en person med et mentalt kart over byen ha noe som kan brukes - etter behov – til å lage et nærmest uendelig antall ruter som kan følges fra startpunkt til endepunkt, så lenge disse ligger på hennes mentale kart. Og hvis hun tar en feil vei, så vil hun fortsatt vite hvor hun er og vil dermed kunne finne frem dit hun skal; og kanskje kan hun også lære noe i prosessen.

Analogien mellom dette og læring i matematikk er nokså tett. Elever som har utviklet instrumentell forståelse har lært en rekke bestemte instrukser som de kan bruke for å komme seg fra spesifikke startposisjoner (oppgaver) til endepunktene (svarene på oppgavene). Elevene har ikke utviklet en forståelse av de underliggende relasjonene mellom de forskjellige stegene og endepunktet, og de er avhengige av ekstern veiledning for å lære seg måter å “komme seg frem” på. I motsetning til dette har elever med relasjonell forståelse bygd mentale strukturer slik at de kan lage nærmest uendelig mange forskjellige planer for å komme seg fra et punkt til et hvilket som helst annet punkt.

Skemps beskrivelse av instrumentell og relasjonell forståelse av matematikk er nært knyttet til det som Hiebert og Lefevre (1986) har kalt henholdsvis prosedyrekunnskap og begrepsmessig kunnskap. De beskriver prosedyrekunnskap som kunnskap om regler og prosedyrer for å løse problemer, ofte i form av oppskrifter for å manipulere symboler. I den norske konteksten har det blitt påpekt at denne typen kunnskap ofte er dominerende i matematikklasserom, særlig når det gjelder algebra (Naaslund, 2012).

Videre beskriver Hiebert og Lefevre (1986) begrepsmessig kunnskap som rik på relasjoner, hvor de bindende relasjonene gjennomsyrer – og er like viktige som - de individuelle bitene med fakta og informasjon. Det finnes mange indikasjoner på at norske elever altfor sjelden får mulighet til å utvikle begrepsmessig kunnskap. Poenget er selvfølgelig ikke at prosedyrekunnskap er verdiløs. Tvert imot, så vil slik kunnskap kunne være nyttig i mange sammenhenger. Poenget er snarere at prosedyrekunnskap alene ikke omfavner essensen i matematikkfaget, og at det ofte bidrar til at elever, med rette, distanserer seg fra faget fordi de ikke ser hensikten i å engasjere seg i et fag hvor de må lære seg tilsynelatende tilfeldige fakta utenat (Eisenhart et al., 1993). Studier viser at det er en sammenheng mellom utvikling av begrepsmessig kunnskap og prosedyrekunnskap.

Forskerne fremhever betydningen av en integrert og balansert utvikling av begreper og prosedyrer i matematikklæring (Bergem, Grønmo, & Olsen, 2005; NCTM, 2014; Rittle-Johnson & Schneider, In press)

Dette skillet mellom to typer kunnskap/forståelse har lenge stått sentralt i det matematikkdidaktiske forskningsmiljøet. Selv i forbindelse med mer avansert matematikk kan vi finne lignende distinksjoner. APOS teori (Dubinsky & McDonald, 2002), som retter seg mot matematikklæring på universitetsnivå, beskriver en prosess der studenten beveger seg gjennom stegene Action, Process, Object og Schema. Uten å gå inn på detaljene i denne teorien er det verdt å merke seg at stegene Action og Process i stor grad minner om instrumentell/prosedyre-læring, mens studentene som har nådd stegene Object og Schema er i stand til å se nettopp relasjonene mellom matematiske fenomener.

Hvordan kan relasjonell forståelse fremmes?

I en analyse av forskning om undervisningens effekt på elevenes læring identifiserer Hiebert og Grouws (2007) to faktorer ved matematikkundervisningen som fremmer elevers relasjonelle/ begrepsmessige forståelse:

1) Eksplisitt fokus på sammenhenger mellom matematiske ideer, fakta og prosedyrer. Dette kan innebære å la elevene arbeide med oppgaver hvor de må finne sammenhenger, diskutere den matematiske meningen bak prosedyrene, stille spørsmål om likheter og forskjeller mellom løsningsstrategier, diskutere hvordan matematiske problemer bygger på hverandre, arbeide med sammenhenger mellom matematiske ideer og gjøre elevene oppmerksomme på læringsmålet med timen og hvordan det de har lært passer sammen med tidligere timer og ideer (s. 383).

2) La elever få streve med viktige matematiske ideer Å streve handler her om at elevene må gjøre en innsats for å forstå matematikken, de må gjøre en innsats for å finne ut av noe som de ikke umiddelbart ser løsningen på. Å streve med viktige matematiske ideer er det motsatte av å simpelthen bli presentert for informasjon som man skal huske utenat eller å bli spurt om å bare praktisere noe man har fått demonstrert (s. 387-388).

Matematikkoppgaver som er kognitivt krevende fremmer større begrepsmessig forståelse hos elevene. I de senere årene har også matematiske diskusjoner og kommunikasjon blitt fremhevet som avgjørende faktorer for utvikling av begrepsmessig forståelse (Anthony & Walshaw, 2009; Cobb, Boufi, McClain, & Whitenack, 1997, Chapin, O’Connor, & Anderson, 2009, NCTM, 2014). Carpenter, Franke og Levi (2003) påpeker at:

Students who learn to articulate and justify their own mathematical ideas, reason through their own and others’ mathematical explanations, and provide a rationale for their answers develop a deep understanding that is critical to their future success in mathematics and related fields. (p. 6)

Lærerens rolle i helklassediskusjoner vil være å hjelpe elevene til å se sammenhenger mellom de ulike fremgangsmåtene og til å se sammenhenger mellom disse og de matematiske ideene som utgjør læringsmålene for timen (Stein et al, 2008).

Forståelse i algebra

Algebra representerer kanskje den delen av skolematematikken hvor vi oftest og mest systematisk støter på algoritmer og huskeregler for å løse problemer, og mange norske elevers forståelse av algebra forblir gjerne på et instrumentelt nivå (Naalsund, 2012). Likevel har algebra, i sin fulle forstand som “the reunion of broken parts” (Schwartzman, 1994; Lesser, 2000), så mye mer å tilby. Artikkelen ”Habits of mind”, som er skrevet av Cuoco og kolleger (1996) har på mange måter blitt en klassiker innen matematikkdidaktisk litteratur, og forfatterne insisterer på at snarere enn å være en passiv, instrumentell aktivitet, så må arbeid med algebra innebære følgende:

• Elever bør være ”mønstersniffere”. Vi bør fremme en glede hos elevene ved å finne skjulte mønstre. (p. 378) 
  
  
• Elever bør være ”beskrivere” (p. 379). De bør være i stand til å gjøre slike ting som å
  • Gi presise beskrivelser av stegene i en prosess. Å beskrive det du gjør er et viktig trinn for å utvikle forståelse.
  • Finne på notasjon. En måte å få elever til å se nytteverdien og elegansen i tradisjonell matematisk formalisme er å la dem få streve med å beskrive fenomener hvor vanlige språklige beskrivelser kommer til kort eller blir for kronglete.
  • Argumentere. Elever bør være i stand til å overbevise sine klassekamerater om at et resultat er riktig eller sannsynlig ved å gi presise beskrivelser av gode beviser/argumenter.
    
    
• Elever bør være utforskere. De bør venne seg til å plukke ideer fra hverandre og sette dem sammen igjen. Når de gjør dette bør de prøve å se hva som skjer hvis noe blir tatt ut eller hvis delene blir satt sammen på en ny måte. (p. 379)
  
  
• Elever bør være ”oppfinnere”. En viktig ingrediens i matematisk oppfinnsomhet er at elever begynner å se etter forskjellige tilfeller av samme matematiske struktur.

Mange av disse punktene gjelder arbeid med matematikk generelt, og fokus på disse faktorene vil ikke bare fremme relasjonell forståelse, men vil også forbedre prosedyrekunnskap på en konstruktiv måte, slik at denne kan brukes som et redskap snarere enn til å lede det matematiske arbeidet.

Selvinnsikt og bevissthet (meta-kognisjon)

”Sjølvforståing” er nevnt som et av formålene med matematikkundervisningen, og i denne konteksten er ”metakognisjon” og ”bevissthet” (awareness) relevante begreper som har blitt brukt i den matematikkdidaktiske litteraturen. Veldig enkelt sagt kan ”metakognisjon” bli tolket som det å ”tenke på å tenke” (Metcalfe & Shimamura, 1994), men ordet har over tid blitt tolket på mange forskjellige og komplekse måter og er dermed ikke helt entydig. I tillegg bør det nevnes at mye av litteraturen om metakognisjon innenfor matematikkdidaktikk handler om hvordan metakognitiv aktivitet kan forbedre matematisk prestasjon. Forskning viser at hvis elever venner seg til å tenke over sin egen tankegang i matematiske sammenhenger så har dette en positiv effekt på det matematiske prestasjonsnivået (e.g. Garofalo & Lester Jr, 1985; Montague & Bos, 1990; Cardelle-Elawar, 1992, 1995; Schoenfeld, 1992; Lester, 1994; Mayer, 1998; Desoete, Roeyers, & Buysse, 2001; Goos, Galbraith, & Renshaw, 2002; Kramarski & Mevarech, 2003; Panaoura & Philippou, 2007; Johansen & Myrvang, 2010; Fossbakk, 2010). Dermed blir metakognisjon ofte sett på som et verktøy som kan fremme læring av matematikk.
  
Konseptet “bevissthet” (awareness), derimot, er ikke underlagt matematikken på samme måte. Tvert imot er bevissthet sett på som et sentralt mål i seg selv, et mål som matematisk aktivitet kan lede til. Den matematikkdidaktiske litteraturen som omhandler bevissthet bygger i stor grad på Caleb Gattegnos utsagn om at “only awareness is educable” (Gattegno, 1987, p. 1). Powell (2007) utdyper dette på følgende måte:

In Gattegno’s pedagogical approach, mathematical situations are proposed to learners who, invited to participate actively, become aware, little by little, of the relationships that structure the situations, and at the same time understand better the dynamics of their own mental functionings. (p. 203)

Elever må med andre ord få mulighet til å reflektere over sine egne tankeprosesser slik at de kan forstå og takle hindringene de støter på. Slik bevissthet og selvinnsikt er ikke bare ønskelig i en matematisk kontekst, men er også et mål i den generelle formative utdanningen (eller danningen) til unge mennesker. Men som Hewitt (2001) påpeker:

This kind of awareness is rarely revealed if a student is carrying out a routine task, such as reproducing a process again and again through an exercise, especially if their answers are correct. (p. 41)

Oppgaver som kan løses ved hjelp av kun prosedyrekunnskap og repetisjon bidrar altså ikke til å fremme elevers selvbevissthet. Det har til og med blitt påstått at arbeid med slike oppgaver kan bidra til å hindre utvikling av bevissthet hos elevene:

Sets of routine exercises actually attract attention to the doing and away from the construing … to the detriment of awareness. (Mason, 1998, p. 259)

Vi ser igjen at skillet mellom instrumentell og relasjonell forståelse står sentralt i diskusjonen om hva som kjennetegner god læring og undervisning, og at hvis vi ønsker bevisste elever som tar aktiv del i egen læringsprosess (om vi bruker begrepet ’meta-kognisjon’, ’selvregulering’, ’bevissthet’ eller andre) så kommer instrumentelt, individuelt arbeid alene til kort. For utviklingen av bevissthet innen matematisk arbeid må både individuelle faktorer, sosiale faktorer og omgivelsene tas i betraktning (Kim, Park, Moore & Varma, 2013), og muligheten til å arbeide undersøkende i små grupper bidrar positivt til denne utviklingen (Magiera & Zawojewski, 2011). Man må også unngå tanken om at meta-kognisjon og bevissthet tar fokus ”vekk fra faget”, for dette er noe som i høyeste grad bør anses som en del av faget, snarere enn noe som kommer i tillegg (Hopfenbeck, 2011).

Motivasjon

Det er gjort mye forskning omkring matematikk og affekt, og sentrale begreper innen dette feltet er holdninger, forestillinger, følelser, verdier, motivasjon og identitet. I denne rapporten vil vi fokusere på elevers motivasjon i matematikk og forskningen som er gjort omkring dette. At motivasjon har stor betydning i matematikkopplæringen er godt dokumentert (Hannula, 2006; Pantziara & Philippou, 2007), og teoretikere hevder at motivasjon har en avgjørende betydning for om elevene lykkes eller ikke i skolen (Cury, Elliot, Fonseca, & Moller, 2006; Pintrich, 2003).

De fleste motivasjonsteoretikere ser i dag på motivasjon som en situasjonsbestemt tilstand som påvirkes av forskjellige faktorer, som klasseromsinteraksjoner, aktiviteter, erfaringer og kultur (Pintrich, 2003; Skaalvik & Skaalvik, 1998). Lærerens undervisningspraksis har derfor stor betydning for elevenes motivasjon. I denne rapporten fokuserer vi på to motivasjonsteorier, nemlig selvbestemmelsesteori og målorientering.

Selvbestemmelsesteori skiller mellom indre og ytre motivasjon. En elev som er indre motivert arbeider med en aktivitet fordi han synes aktiviteten er interessant og morsom i seg selv. Dersom eleven utfører en handling for å oppnå et resultat som er atskilt fra selve aktiviteten, er hun ytre motivert. (Ryan & Deci, 2000a). Forskning har vist at det er mange fordeler knyttet til indre motivasjon (Gottfried, 1985; Ryan & Deci, 2000b). Elever som er indre motiverte for skolearbeidet, er mer utholdende, har større selvtillit, er mer kreative og benytter i større grad problemløsningsstrategier enn elever som er ytre motiverte. Indre motivasjon er også assosiert med mer glede, aktiv involvering og kognitiv fleksibilitet enn ytre motivasjon (Pintrich, 2003; Ryan & Deci, 2000b; Stipek, 1996; Stipek, Salmon, Givvin, & Kazemi, 1998).

For å forstå elevenes motivasjon må vi kjenne deres mål (og disse kan variere fra elev til elev). Mange motivasjonsteoretikere skiller mellom to typer målorientering, nemlig læringsorientering og prestasjonsorientering. Læringsorientering betyr at læring er et mål i seg selv. Målet er å utvikle forståelse og ferdigheter eller få mer innsikt. Prestasjonsorientering betyr at eleven er opptatt av seg selv i læringssituasjonen og målet er å bli oppfattet som flinkere enn andre i matematikk (Andrew J. Elliot, 2005). Forskning har vist at det er en sammenheng mellom læringsmål og elevenes adaptive oppfatninger, som inkluderer forventing om mestring, prestasjoner og interesse (Anderman, Patrick, Hruda, & Linnenbrink, 2002; Cury et al., 2006; A. J. Elliot & Church, 1997). Forskning på prestasjonsmål er mindre konsistent, men elevenes prestasjonsorientering har blitt assosiert med lave prestasjoner, frykt for å gjøre feil og overfladisk kognitiv forpliktelse, som for eksempel å kopiere, repetere og huske utenat (Cury et al., 2006).

Flere studier har undersøkt hvordan matematikklæreren og klasseromskulturen kan påvirke elevenes motivasjon. Resultatene indikerer at det finnes seks aspekter ved klasseromskulturen som påvirker elevenes motivasjon i matematikk på en positiv måte, i form av økt indre motivasjon og læringsorientering (Anderman et al., 2002; Boaler, 1997, 2004; Cobb, Wood, Yackel, & Perlwitz, 1992; Mendick, 2002; Nicholls, Cobb, Wood, Yackel, & Patashnick, 1990; Pantziara & Philippou, 2007, 2010; Schukajlow & Krug, 2014; Stipek et al., 1998; Turner et al., 2002; Wæge, 2007, 2008):

1. Oppgaver og aktiviteter, som problemløsningsoppgaver, praktiske oppgaver, oppgaver fra dagliglivet og åpne oppgaver.
2. Samarbeid.
3. Elevene blir oppmuntret til å utvikle egne løsningsstrategier (autonomi).
4. Et positivt affektivt klasseromsmiljø (læreren behandler eleven med respekt, lytter til ideene deres og verdsetter deres faglige bidrag).
5. Fokus på læringsprosessen og utvikling av forståelse i matematikk.
6. Læreren gir konkrete og konstruktive tilbakemeldinger, utfordrer elevene og bruker feil og misoppfatninger som en del av læringsprosessen.

Disse resultatene samsvarer med mer generell forskning om elevers indre motivasjon og målorientering (Pintrich, 2003; D. J. Stipek, 1996).

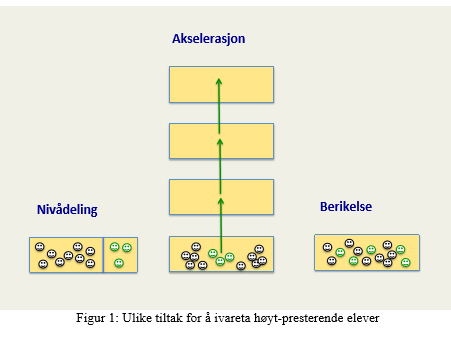
Tilpasset opplæring – nivådeling, akselerasjon eller berikelse?

Tilpasset opplæring er et viktig prinsipp i norsk skole, og hvordan vi skal møte høytpresterende elevers læringsbehov er et svært aktuelt tema i Norge for tiden. Sentrale spørsmål i denne sammenhengen er om elever bør undervises i nivådelte grupper, om høyt-presterende elever bør tilbys et forsert/akselerert løp, eller om vi bør forsøke å tilfredsstille deres behov innenfor det ordinære klasserommet ved å arbeide med matematiske aktiviteter som kan gi alle elever, uansett prestasjonsnivå, passende utfordringer. Med andre ord, ønsker vi å vektlegge nivådeling, akselerasjon eller berikelse?

Figur 1 viser disse tre mulige – og i flere land ofte brukte - tiltakene for å ivareta høytpresterende elever. Slik vi bruker begrepene her referer nivådeling til en praksis som deler elever i en klasse opp i (fysisk separerte) grupper basert på estimert nivå, og disse gruppene undervises hver for seg. Akselerasjon referer til det å la elever ta matematikk på et nivå som tilsvarer pensum en eller flere klasser over. Med andre ord blir elevene forsert ”oppover” gjennom skolesystemet, enten i egne grupper eller ved å la dem ta del i undervisningen til eldre klasser. For eksempel kan elever i 10. klasse få tilbud om å ta 1T matematikk.

Med berikelse i klasserommet mener vi her en praksis der differensiert og tilpasset undervisning foregår i heterogene klasser, og fokus rettes mot rike oppgaver som har lav inngangsterskel, og hvor det i tillegg er mulig for elevene å arbeide på ulike nivåer.

Nivådeling

Mange studier om nivådeling har fokusert nesten utelukkende på elevers prestasjoner (se for eksempel Burris, Heubert & Levin, 2006; Burris, Wiley, Welner & Murphy, 2008). Disse studiene viser at nivådeling gir marginale positive effekter for høyt-presterende gruppers prestasjoner, mens det samtidig har signifikante negative effekter for de lavt-presterende gruppene.

I de senere årene har mange forskere bemerket at større fokus må rettes mot elevers læring (ikke bare prestasjoner målt på prøver). Studier om nivådeling med fokus på læring (eg. Boaler, William & Brown, 2000) har vist at ”Homogene” klasser i matematikk svekker elevenes motivasjon og fører til redusert selvtillit hos både høyt-presterende og lavtpresterende elever. Resultatene viser videre at ”Homogene” grupper med høyt-presterende elever har negative følger på grunn av høyt tempo, høyt press og fokus på prosedyrer:

• Misnøye og mindre glede av matematikk, spesielt hos jenter
• Lavere presentasjoner enn forvente
• Høyt tempo hindrer forståelse

Også de sosiale konsekvensene av nivådeling har det blitt forsket mye på, og disse har vist seg å være markante. Nivådelingen følger i de aller fleste tilfeller elevenes sosiale, økonomiske, og i visse tilfeller også etniske bakgrunn, og fører til re-produsering av forskjeller i både økonomi og ’kulturell kapital’ (Boaler, 1997b; Faulkner, Stiff, Marshall, Nietfeld & Crossland, 2014).

Akselerasjon eller berikelse

Feng (2005) har bemerket at det til tider kan være vanskelig å skille mellom akselerasjon og berikelse som begreper, fordi begge ofte har blitt foreslått som tiltak for høyt-presterende elever. Det er likevel viktig å kjenne til forskjellen mellom de to begrepene ettersom målene og utfallene som er assosiert med dem er ganske forskjellige. Svaret på om akselerasjon er et godt tiltak kommer an på hva man ser på som essensen matematikkfaget. Som Renzulli (1979) har bemerket,

”Unless additional provisions are made for individual investigative activity, a treadmill is a treadmill even when run at a faster pace.”

Hvis målet er økt relasjonell forståelse i matematikk så er det ikke ønskelig at tiltak for høytpresterende elever i prinsippet går ut på å la dem jobbe raskere og med mer komplekse oppgaver med fortsatt instrumentelt fokus. Dessverre er dette nesten utelukkende tilfellet i en akselererende praksis. Tilbudet om forsering er blitt svært populært i Norge, og på noen skoler oppleves stor pågang for dette, særlig mot slutten av ungdomsskolen. Da faller det naturlig å vurdere om tiltak må til på ethvert klassetrinn for å heve basistilbudet, i stedet for å stadig forflytte elever oppover. For vi snakker her om en relativt stor gruppe elever og ikke en liten minoritet.

Spørsmålet om satsing på akselerasjon eller berikelse er også tett knyttet til forskjellen mellom instrumentell og relasjonell læring. Hvis matematikkundervisningen i hovedsak består av prosedyrebaserte oppgaver som kan løses etter gitte regler, er det naturlig at spørsmål om akselerasjon dukker opp. Noen elever kan løse slike oppgaver raskere enn andre og bør dermed beveges “opp” i systemet. Et viktig spørsmål vi må stille oss er om dette fremmer elevenes relasjonelle forståelse i matematikk.
  
Jahr (2000) hevder at det ikke er noen motsetning mellom det å gi lavt-presterende elever passe utfordringer og samtidig stimulere høyt-presterende elever i matematikk. Å dele inn elevene ut fra nivå og gi høyt-presterende elever mer avanserte oppgaver er en dårlig løsning, påpeker han, det er helt avgjørende at elevene innenfor samme årstrinn arbeider med det samme materialet. For å illustrere poenget sitt, bruker Jahr eksempelet med et menneske som går tur med hunden sin:

Hunden løper mye fortere enn sitt menneske, men den løper ikke rett hjem og sitter der og venter i timevis. Den går samme tur som oss, men snuser borti så mye mer; under røtter, i maurtuer, bak hvert tre. Et er altså mulig å lære mer enn sine turkamerater på den samme turen, uten å miste kontakten! (Jahr, 2000, s. 82)

I tillegg fremhever Jahr at det også er viktig at de flinke elevene lærer å dele sin ”flinkhet” med andre:

det å være flink medfører noe omsorgsansvar. Skal vi kune skape et samfunn som tar vare på de svake, må noen være flinke. Uten at man driver rovdrift på dem, bør de kunne fungere som ”hjelpelærere” av og til. Ofte må de da reflektere over spørsmål som de ikke har trengt å stille før, fordi de bare har fått til oppgavene uten videre. (s. 83)

Ved å la elevene arbeide med mer åpne, kognitivt krevende og undersøkende aktiviteter i matematikk, kan høyt-presterende elever få mulighet til å lære på det nivået som passer dem, uten å måtte separeres fra sine klassekamerater. Deres opplevelse av matematikk kan bli beriket ved å gi dem mulighet til å utforske andre og kanskje mer detaljerte aspekter ved de samme matematiske situasjonene. Det kan også fremme deres utvikling av relasjonell forståelse i faget. Dette trenger ikke å skje i separasjon fra de andre i klassen. Med andre ord trenger ikke berikelse å innebære en nivåinndeling av elever på samme trinn. Målet er snarere differensiert undervisning i heterogene klasser, der det er mulig for elever å utforske forskjellige aspekter av samme tema (se for eksempel Wæge, 2007).

Utfordringer

Det er viktig å bemerke at det å ivareta høyt-presterende elever i en heterogen gruppe er en krevende oppgave. Lærere mener selv at de har kompetanse i å undervise høytpresterende elever, men forskning viser at det ikke er samsvar mellom lærernes syn og praksis i klasserommet på dette området. Men selv om utfordringene er mange, og høye krav må stilles til en lærer som skal lykkes i å differensiere i en heterogen klasse, så tilsier forskning at dette er den mest fordelaktige praksisen for alle elevgrupper. (Se for eksempel Shayshon, Gal, & Ko, 2014).

Diskusjon  

I de foregående seksjonene har vi beskrevet en rekke faktorer som kjennetegner god matematikklæring og undervisning. Flere av disse faktorene inngår i det som mange forskere de senere år har definert som målet med matematikkundervisningen, nemlig utviklingen av ”mathematical proficiency”, eller ”matematisk kompetanse”, hos alle elever. Matematisk kompetanse beskrives ved hjelp av fem komponenter; forståelse, beregning, anvendelse, resonnering og engasjement, som er tett knyttet sammen og avhengige av hverandre (Kilpatrick, Swafford & Findell, 2001). Dette ambisiøse målet fører til nye definisjoner av lærernes arbeid:

Ambitious teaching supports mathematical meaning making, identity building, and equitable opportunities to learn. It requires a teaching practice that allows teachers to engage deeply with children’s thinking; that creates robust opportunities for all children to learn; that supports meaningful participation in mathematics for all children; and that disrupts longstanding assumptions about who can and cannot do math. (Kazemi, Cunard & Crowe, 2012)

Kazemi et al. påpeker videre at lærerne må ta utgangspunkt i elevenes tenking. De må stille spørsmål, observere og tolke elevenes resonnering, språk og argumenter og, basert på dette, tilpasse undervisningen for å fremme elevenes læring. Denne visjonen av ”ambitous teaching” bygger på en økende mengde forskning fra de siste tretti årene som gjerne fremhever bruken av undersøkende arbeidsmetoder.

I en undersøkende undervisningskontekst setter læreren opp læringsmålene, men lar elevene selv utforske problemene for å finne mønstre og systemer. Elevene driver aktiv matematisk utforskning og diskuterer egne løsningsstrategier med hverandre. Feil anses som en naturlig del av læringsprosessen. Når elevene får lov til å utforske et felt og diskutere hvordan de tenker med hverandre, oppdager de at matematikk slett ikke er et fag som kun består av å huske hva læreren har sagt. I stedet blir det til et spennende og aktivt fag som består av utforskning på elevenes egne premisser.

Faktorene som har blitt diskutert i denne rapporten bør etterlate liten (eller snarere ingen) tvil om at god matematikkundervisning er et ekstremt krevende arbeid hvor god holdning og høy kunnskap om både matematikk og elevers læring er uunnværlig. Et yrke med slike høye krav bør bli lønnet og belønnet deretter, og arbeidet med å oppnå “ambitious teaching” for alle elever henger tett sammen med arbeidet med å heve læreryrkets status til et nivå hvor det blir ansett for å være et av de mest populære og prestisjefulle yrkene som finnes.