Skoleferdigheter i endring: Utviklingen over tid målt ved nasjonale prøver

Innledning

Ifølge offisiell statistikk, basert på årlige nasjonale prøver for lesing, regning og engelsk på både 5. og 8. trinn, var norske elevers gjennomsnittlige ferdigheter tilnærmet uendret i årene 2014–2021. Vi ettergår denne konklusjonen ved hjelp av fullstendige, anonyme data på oppgave-elev-nivå.

Vi ønsket opprinnelig å bruke mikrodata for å undersøke hvordan pandemitiltak som nettbasert «fjernskole» og utbruddsrelaterte skolestengninger påvirket læringsutbyttet under covid. Men de nasjonale prøvene indikerer ingen konsekvenser av betydning, i klar kontrast til funn fra både internasjonal forskning (Blanden et al., 2022) og en norsk publisert studie (Skar et al., 2022). Norske elever oppnådde 50 skalapoeng i snitt i alle år fram til 2021, i alle de tre fagene og på begge klassetrinn. Unntaket er engelsk på 5. trinn i 2021 med 51 poeng.

En slik stabilitet over åtte år er overraskende, ettersom barn og ungdoms hverdag utenfor skolen er i stadig endring på måter som ville forventes å påvirke disse ferdighetene. Barn og unge bruker mindre tid på bøker enn før (SSB, 2012), har bedre utdannede foreldre enn tidligere, og eksponeres stadig mer for engelsk gjennom sosiale medier og dataspill. I tillegg har en økende andel av elevene utenlandsk bakgrunn. Lærere og språkforskere forteller at de mener å observere en dramatisk økt engelskkompetanse i nyere år (Aftenposten, 2022). Stabilitet i gjennomsnittlige ferdigheter er ikke umulig i en slik kontekst, men var like fullt overraskende for oss.

De årlige prøvene («Nasjonale prøver») er utviklet basert på Item Response Theory (IRT) der målet er å anslå et ferdighetsnivå for hver enkelt elev langs en endimensjonal skala (Lord, 1952; Embretson & Reise, 2013). Prøvene er administrert på en måte som gjør det mulig å holde måleskalaen konstant over tid slik at skår kan sammenliknes både innad i og på tvers av prøve-år. Dette er gjort ved at en tilfeldig trukket undergruppe («ankerelever») får erstattet deler av oppgavesettet med ikke-offentliggjorte oppgaver som også tidligere års ankerelever har besvart («ankeroppgaver»). Elevens ferdighet er angitt i «skalapoeng» og normert til å ha et snitt på 50 og standardavvik på 10 i første elevkull.

Vi begynner med en oppsummering av vår studie. Kalibreringen av ulike års prøver til en felles skala er teknisk, og det er krevende å ettergå hvordan de offisielle tallene er beregnet. Samtidig er prøvene utformet på en måte som legger til rette for også enklere og mer intuitive mål på tidsutviklingen. Siden ankeroppgavene gjenbrukes og besvares av tilfeldig trukne ankerelever i hvert kull er det rett fram å se om ankerelevene gjør det bedre eller dårligere over tid på disse. En slik analyse har en kort og oversiktlig vei fra data til resultat, og gir en enkel og rask pekepinn på rimeligheten i resultater fra en mer innfløkt sammenlikningsmetodikk.

Med anonyme data på elev-oppgavenivå fra Utdanningsdirektoratet (Udir) for alle nasjonale prøver i 2014–2021 med kjønn som eneste elevkjennetegn presenterer vi tre analyser av tidsutviklingen:

1. Tidsutvikling på ankeroppgavenivå der vi beregner andelen ankerelever hvert år som besvarer de ulike ankeroppgavene korrekt.
2. Gjennomsnittlig utvikling over ankeroppgaver der vi simultant analyserer alle ankeroppgaver i et fag på et bestemt trinn ved hjelp av lineære regresjonsmodeller.
3. Gjennomsnittlig skalapoeng år for år på felles skala ved av hjelp IRT-modeller.

De tre analysene er basert på ulike antakelser og bruker til dels forskjellige deler av data. De to første benytter kun ankerelevene og forutsetter at disse faktisk var tilfeldig trukket. IRT-analysen er basert på alle elevene, hvor det kun er nødvendig at ankerelevene dekker alle ferdighetsnivåer. Denne analysen bygger på det samme teoretiske rammeverket som Udir har benyttet og med samme målsetting som de offisielle tallene.

Uavhengig av metode og utvalg kommer vi til samme konklusjon. Norske elevers ferdigheter i både lesing, regning og engelsk har endret seg vesentlig, med en særlig markant forbedring i engelsk på både 5. og 8. trinn. For lesing og regning er endringene mindre, men vi ser en trend med svakt fall i ferdighetene etter 2016.

For å forstå hvorfor de offisielle tallene avviker fra våre, gikk vi nærmere inn i hvordan IRT-modeller historisk har blitt implementert. Udir benyttet programmet XCalibre for IRT-beregningene fram til 2021 og har gjort enkelte kontrollfiler og rapporter fra denne programvaren tilgjengelig for oss. Vårt inntrykk er at analysene ble spesifisert i tråd med programvarens brukerhåndbok.

Vi er i stand til å replikere Udirs analyser og finner eksakt de samme resultatene som de offisielle tallene for regning. Deretter gjennomførte vi en simulering med konstruerte data der vi kjenner «fasiten» og kan teste ulike modellspesifikasjoner på en kontrollert måte. Denne viser at XCalibre ikke er i stand til å avdekke endringer i ferdigheter over tid. Årsaken er at programvaren Udir brukte, la til grunn at ferdighetene hvert år trekkes fra den samme standardiserte fordelingen. Det er åpenbart umulig å avdekke endring i ferdigheter på tvers av årskull dersom man starter med å legge til grunn at kullene, i forventning, er helt like.

For å sikre etterprøvbarhet og transparens er all programkode gjort tilgjengelig i vedlegg. Vi har ikke tillatelse til å dele de anonyme rådataene, men Udir opplyser at interesserte kan henvende seg til dem for tilgang.

Tidsutviklingen i norske elevers ferdigheter

Ettersom eksamens- og standpunktkarakterer både normeres og utsettes for «karakterinflasjon», finnes det få kilder til «objektiv» tallfesting av endringer i norske elevers kompetanse over tid. En sentral kilde til slike data er nasjonale prøver, der det er en uttalt målsetting fra utdanningsmyndighetene at skalaen på ulike års prøver skal være den samme. Dette ble innført i 2014 gjennom et ankerdesign og skalaen til de nasjonale prøvene er normert på bakgrunn av elevene i det første årskullet. Gjennomsnittprestasjonen i 2014 ble definert som 50 skalapoeng, og standardavviket i elevkompetansen ble pålagt å være 10 skalapoeng. Enhver utvikling i skalapoeng deretter må altså sees i forhold til dette: Dersom gjennomsnittet i 2020 skulle bli 55 skalapoeng, betyr det at gjennomsnittseleven dette året var like dyktig som en elev et halvt standardavvik over snittet i 2014. Går man inn i Udirs eller SSBs statistikkbank, kan man hente ut tall for gjennomsnittlige skalapoeng på alle prøver etter fag og trinn (tabell 1).

Tabell 1. Gjennomsnittlig skalapoeng etter år, trinn og fag, 2014–2021

Note: Kilde er «10793: Gjennomsnittlig skalapoeng på nasjonale prøver, etter klassetrinn, prøve, innvandringskategori, kjønn, statistikkvariabel og år» i SSBs statistikkbank. Skalapoengene publiseres uten desimaler og usikkerhetsanslag. Merk at poengene for lesing i 2014 og 2015 ikke måles på samme skala siden ankersystemet i lesing startet først i 2016.

Tabell 1 viser at gjennomsnittlige ferdigheter ikke har endret seg fra 2014 til 2021, med ett unntak for engelsk på 5. trinn i 2021. Riktignok er tallene i statistikkbanken rundet av til nærmeste heltall, men selv en utvikling innen intervallet mellom 49.5 og 50.5 må kunne sies å være svært stabil. Et standardavvik i fordelingen (også fastsatt i 2014) er 10 poeng slik at utviklingen har altså vært innenfor +/– et tyvendedels standardavvik.

Denne oppsiktsvekkende stabiliteten kan sammenholdes med anslag på tidsutviklingen fra andre datakilder. Internasjonale studier som PISA (Programme for International Student Assessment), TIMSS (Trends in International Mathematics and Science Study) og PIRLS (Progress in International Reading Literacy Study) er konstruert for sammenlikninger både mellom land og innen land over tid. PISA viser at norske 15-åringers kunnskaper i lesing, matematikk og naturfag har svingt rundt et stabilt nivå fra 2000 til 2018 (Jensen et al., 2019). I 2018 var resultatene for både lesing og naturfag signifikant svakere enn i 2015, mens norske 15-åringer var like gode i matematikk som tre år før. De nylig publiserte PISA-resultatene viser en ytterligere tilbakegang sammenliknet med fire år tidligere i alle de tre fagområdene (Jensen et al., 2023).

Norske elever har deltatt i TIMSS (Trends in International Mathematics and Science Study) siden 1995, men en endring i deltakende alderskull gjør at kun resultater for 2015 og 2019 er sammenliknbare. For 9. trinn var kompetansen signifikant svakere i 2019 enn fire år tidligere i både matematikk og naturfag. Tilbakegangen var betydelig ettersom den «anslås til ca. et halvt års skolegang i naturfag og et tredjedels skoleår i matematikk» (Kaarstein et al., 2020, s. 5). For 5. trinn finner TIMSS ingen signifikante endringer i kompetansen i verken matematikk eller naturfag fra 2015 til 2019.

Lesing på barnetrinnet har blitt målt i PIRLS siden 2001 og norske elever økte sine leseferdigheter jevnt og trutt fra 2006 og fram til 2016. Denne trenden ble imidlertid brutt i 2021 da leseferdighetene hos norske tiåringer falt betydelig fra 2016 og var tilbake på nivået fra 2006 (Wagner et al., 2023). Tilsvarende utvikling ser vi også i de andre nordiske landene.

For engelsk (første fremmedspråk) finnes ingen internasjonale studier med tilsvarende pålitelighet som kan kaste lys over utviklingen i kompetansen hos norske barn og ungdom. Mens endring i gjennomsnittlige ferdigheter er vanskelig å måle, finnes det en rekke studier som kartlegger hvordan kjønnsforskjell i andrespråkskompetanse (oftest engelsk) har endret seg, delvis motivert utfra at økt utbredelse av sosiale medier og online-spill i ulik grad påvirker gutter og jenter. Foreldre og lærere opplever av norske barn og ungdom mestrer engelsk langt bedre enn før (Aftenposten, 2022), men oss bekjent finnes ingen vitenskapelig studie som viser dette.

Oppsummert viser altså andre kilder betydelig variasjon over tid i ulike ferdigheter. De siste årene avdekker både PISA og PIRLS en trend der ferdighetene i gjennomsnitt er fallende. Også derfor er stabiliteten som oppgis for nasjonale prøver oppsiktsvekkende.

Ankeroppgaver og sammenliknbarhet over tid

En sammenlikning av elevers fagkompetanse på tvers av årskull er ingen triviell oppgave, ettersom vi mangler en objektiv og fast målestokk. En elev som måler 160 centimeter og veier 50 kilo i dag er like høy og tung som en med samme mål i 1970, men elever som får 75 % riktig på en engelskprøve i dag er de ikke dermed på samme nivå som noen som fikk 75 % rett på en engelskprøve i 1970. Den første utfordringen er at det vi skal måle, ferdigheter eller kompetanse, ikke er direkte observerbart. Dette er forsøkt løst ved å utvikle et måleinstrument – et batteri av ulike oppgaver som alle speiler den underliggende ferdigheten en ønsker å måle. De ulike fagmiljøene som er involvert legger stor innsats i å lage og teste ut oppgaver benyttet i de nasjonale prøvene, nettopp for å sikre at de ulike oppgavene i sum gir et godt mål på den underliggende ferdigheten vi er interessert i (NOU 2023:1, s. 88). Oppgavene skal for eksempel ha et stort spenn i vanskegrad, slik at ulike elevers ferdighetsnivåer kan avdekkes ved å se hvor krevende oppgaver må bli før de faller av.

Den neste utfordringen er at for å kunne sammenlikne ferdigheter over tid må en ha et måleinstrument som er konsistent over tid. En åpenbar løsning på dette er å benytte det samme instrumentet. Men skal disse oppgavene benyttes om igjen over flere år er det viktig at oppgavene ikke blir kjent for dem som ikke har tatt prøven ennå. Dette gir ytterligere en utfordring i de nasjonale prøvene: Det er ønskelig at prøven i etterkant skal benyttes som et pedagogisk verktøy og gjennomgås av lærer sammen med elevene. Samtidig må en unngå at lærere oppnår bedre prøveresultat for sine elever ved å la elevene på forhånd pugge svarene. Dette tilsier at det må lages nye oppgaver hvert år, men da mister man muligheten for å måle konsistent på tvers av år.

Løsningen på dette, som ble innført fra og med 2014 for engelsk og regning og i 2016 for lesing, er en tilnærming som kalles horisontal lenking (Bjørnsson, 2018). Denne plasserer forskjellige prøver med liknende egenskaper på en felles skala (Kolen & Brennan, 2014). I praksis har dette blitt gjort ved å trekke et tilfeldig utvalg på om lag 3500 «ankerelever» som gjennomførte en to-delt prøve (Björnsson, 2018). Ankeroppgavene som holdes hemmelig og benyttes i flere år, inngår sammen med oppgaver fra årets oppgavesett. Ankerdesignet kan derfor forstås som et praktisk kompromiss som legger til rette for sammenlignbarhet over tid, samtidig som prøveresultatene er et pedagogisk verktøy.

En ytterligere utfordring, som ikke relaterer seg til ankersystemet spesielt, er at oppgavene som gis til forskjellige elevkohorter bør avspeile underliggende ferdigheter likt på tvers av kohorter, eksempelvis at de er like vanskelige. Når vi kobler sammen prøver over tid, kan enkeltoppgaver bli lettere/vanskeligere å besvare med den samme underliggende ferdigheten. Å regne med sedler og mynter eller si hvor lang tid som er gått mellom to urskiver med visere i ulike posisjoner er vanskeligere for elever som først og fremst kjenner til digitalur og betalingskort, men dette betyr ikke dermed at de har dårligere regneferdigheter. Dersom oppgaver endrer vanskegrad, vil vi få parameterdrift (Goldstein, 1983) som man må ta hensyn til for å unngå skjevhet i skalaen når man kobler sammen prøver for ulike kohorter over tid.

Metodiske rammeverk for måling av kompetanse over tid

Selv om IRT-rammeverket dominerer analyser av ferdighetsmønstre, finnes det enklere og mer gjennomsiktige metoder som kan benyttes for å avdekke mønstre i dataene fra de nasjonale prøvene. Innledningsvis starter vi med en enkel lineær regresjonsmodell som i praksis gir estimater utfra forskjeller i riktige svar på ankeroppgaver fra ett kull til det neste. Siden denne ga resultater som avvek betydelig fra de offisielle tallene, gikk vi også videre og estimerte hele kompetansefordelingen ved hjelp av en korrekt spesifisert IRT-modell. Mens den lineære sannsynlighetsmodellen kun er identifisert ut fra svarene på ankeroppgavene, er IRT-modellen estimert på hele oppgavesettet for alle elevene. Utdanningsdirektoratet brukte IRT-rammeverket for sine anslag, men våre analyser vil vise at valg av eksakt modell innen «IRT-familien» er avgjørende for å få korrekt svar. Et intuitivt og enkelt mål på kompetanseutviklingen fra ett år til et annet er den gjennomsnittlige endringen i andelen rett svar på ankeroppgavene. Enkelt sagt: Hvis årets ankerelever har flere riktige svar i gjennomsnitt enn fjorårets så har de bedre ferdigheter. Dette forutsetter at ankeroppgavene måler den underliggende ferdigheten likt over tid, slik at ikke tidsutviklingen forstyrres av oppgaver med parameterdrift. I utgangspunktet bør ikke dette være et problem, ettersom ankeroppgaver skal ha blitt byttet ut der parameterdrift ble påvist. I tillegg ettergås denne antakelsen gjennom grafiske analyser på enkeltoppgavenivå.

Vi benytter et enkelt opplegg der utfallet – svar på en oppgave («item») i en prøve – er modellert ved en lineær sannsynlighetsmodell som vist i likning (1). Oppgavene har ulik vanskegrad, og vi antar at denne er ukjent. For hver av de seks prøvene er sannsynligheten for riktig svar for elev j på oppgave i som del av prøven i år t forklart ved to sett av faste effekter.

Ved å benytte faste effekter for hver ankeroppgave (µi), sikrer vi at all sammenlikning over tid gjøres innen oppgave. Tidseffektene (ηt) uttrykker da om elevenes prestasjoner over tid har endret seg. Uobserverte tilfeldige forhold er målt ved restleddet (εj). Standardfeilene er klyngejustert for person og oppgave. Modellen er estimert i R med pakken fixest (Bergé, 2018) og i Stata 17.

Tidseffektene for andel riktige svar i likning (1) er enkle å forstå, men samtidig har metoden åpenbare begrensninger. Viktigst er kanskje at modellen ikke tillater å estimere hver enkelt elevs ferdighetsnivå, som er helt nødvendig for den pedagogiske bruken av de nasjonale prøvene.

Det metoderammeverket som oftest benyttes til analyser av denne typen data er Item Response Theory (IRT). En IRT-modell antar at svarmønsteret på et sett av oppgaver avspeiler en endimensjonal underliggende kompetanse for hver elev som skal måles (Lord, 1952; Embretson & Reise, 2013). Hver oppgave beskrives med en såkalt responsfunksjon. For skalering av de nasjonale prøvene har Udir brukt en såkalt en 2-parameter logistisk (2PL) modell (Udir, 2022) . For 2PL-modeller brukes responsfunksjonen som er vist i likning (2).

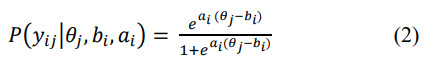
I denne funksjonen beskriver P sannsynligheten for at elev j med ferdighetsnivå
θj svarer riktig på oppgave i med vanskegrad bi og diskrimineringsevne lik ai. Siden det er en uendelig rekke skalaer som ville gi samme observerbare svarsannsynlighet, blir prøven normert ved å definere en skala ut fra resultatene til de som tar testen. Ved estimering av en IRT-modell tas det utgangspunkt i en θ-skala hvor gjennomsnittet er 0 og standardavviket er 1. For de nasjonale prøvene har denne skalaen blitt lineært transformert, slik at gjennomsnittsferdigheten er 50 poeng med et standardavvik på 10 poeng i det første test-året (2014).

Når ulike årganger av en prøve skal kobles til skalaen etablert i referanseåret, kan dette gjøres med ulike statistiske lenkemetoder. Udir oppgir å ha brukt en tilnærming kalt «Fixed common item parameters» (FCIP; Li et al., 1997) for nasjonale prøver i perioden 2014–2021. Her estimeres ankeroppgavenes parametere sammen med resten av oppgaveparameterne i det første teståret. I senere år anser man disse parameterne som kjent. I stedet for at gjennomsnittet og standardavviket defineres for den nye årgangen, gjør ankeroppgavene at de estimeres i forhold til referanseåret. Skalaen for den nye prøven blir dermed lik som for referanseåret, selv om den nye prøven har en annen vanskegrad eller om ferdighetsnivået til populasjonen endrer seg. Det vil si at to elever som har samme ferdighetsnivå vil få samme antall skalapoeng selv om de tar forskjellige prøver, uavhengig om prøvene er like vanskelige og hvordan andre elever har gjort det på prøvene.

Det finnes andre relevante statistiske lenkemetoder. Én av dem er såkalt samkalibrering, der man estimerer både populasjons- og oppgaveparametere for alle årganger samtidig ved hjelp av en fler-gruppe-modell. Med data for flere årganger blir parameterne til ankeroppgavene i de fleste tilfeller mer presist estimert enn ved FCIP (Hanson & Béguin, 2002). En ulempe med samkalibrering er at resultater fra tidligere år vil kunne endres når nye årganger legges til.

Både IRT-modellene og estimeringsmetodene er godt etablert. Våre analyser er gjort i R (R Core Team, 2022), med pakken mirt versjon 1.40 (Chalmers, 2012). FCIP er manuelt implementert, og samkalibreringen er gjort med en fler-gruppemodell. Udir benyttet Xcalibre versjon 4.2.2 (Guyer & Thompson, 2014) for beregningen av de offisielle skalapoengene i perioden 2014–2021.

Data

Det finnes god informasjon hos Udir om hva nasjonale prøver er og hvordan de gjennomføres (Udir, 2022; NOU 2023:1). Vi nøyer oss derfor her med en helt kort og forenklet beskrivelse. Hver prøve gjennomføres på en datamaskin og består av et stort antall oppgaver. Hver av disse oppgavene gir, med få unntak, 1 poeng dersom svaret godkjennes. Siden prøvene gjennomføres digitalt, skåres de også maskinelt.

I utgangspunktet skal alle elever gjennomføre prøven, men det kan gis fritak. Fritak kan gis til elever som har vedtak om spesialundervisning eller særskilt språkopplæring. Omfanget av slike fritak har fått stort oppmerksomhet i offentlig debatt som en mulig forklaring for hvorfor noen kommuner/skoler gjør det bedre enn andre. I snitt er det om lag 5 prosent av elevene som fritas fra prøvene. I tillegg er det 1–2 prosent som ikke gjennomfører prøven av andre grunner.

For ankerelevene utgjør ankeroppgavene om lag halvparten av prøven. Det er omtrent 20–30 slike ankeroppgaver i hver prøve. Oppgavene benyttes i flere år, med noe utbytting av enkeltoppgaver over tid for å håndtere oppgavedrift. I våre data varierer tiden ankeroppgavene inngår, fra 2 til 6 år.

Resultatprolog – Er ankerelevene representative for alle elevene?

I den enkle lineære sannsynlighetsmodellen analyserer vi kun ankerelevenes svar på ankeroppgaver for å anslå hvordan andelen rette svar har utviklet seg fra ett kull til de neste. Når vi tolker dette som en endring i elevkullenes gjennomsnittskompetanse, legger vi til grunn at ankerelevene kan anses som et tilfeldig utvalg fra sitt kull. Dette er en viktig antakelse, men den kan sjekkes ved hjelp av oppgavene som alle elevene besvarer. Siden ankerelevene også besvarer mange av de samme oppgavene som resten av sitt årskull, kan vi bruke disse «kohortoppgavene» til å se om ankerelevenes gjennomsnittlige prestasjoner på felles kohortoppgaver er på linje med snittet til resten av elevmassen det året.

For å undersøke dette estimeres sannsynligheten for riktig svar ved lineær regresjon med faste effekter («konstantledd») for hver enkelt oppgave og en indikatorvariabel for om eleven er «ankerelev» eller ikke. Denne indikatorvariabelen vil ha en koeffisient som ikke er signifikant forskjellig fra null dersom ankerelevene er tilfeldig trukket. Modellen estimeres separat for hvert trinn/fag/år. For hver enkelt elev har vi da like mange observasjoner som vi har oppgaver. For å justere for at vi «blåser opp» datasettet på denne måten, er standardfeilene såkalt to-veis klyngejustert for individ og oppgave. Resultatene er vist i figur 1.

Fra figur 1 ser vi at forskjellen i riktige svar mellom ankerelevene og de andre er på +/– 0.01, hvilket tilsvarer at én ekstra i en gruppe av hundre elever svarer riktig/feil. Dette er svært lite og med unntak av lesing, særlig på 5. trinn, er ingen av forskjellene innad i kull signifikante (på 95 % nivå). Vår konklusjon er at utviklingen over tid ikke er påvirket av skjeve utvalg av ankerelever. Derfor vil en analyse av ankerelevene alene gi et godt grunnlag for å undersøke tidsutviklingen i elevenes ferdigheter.

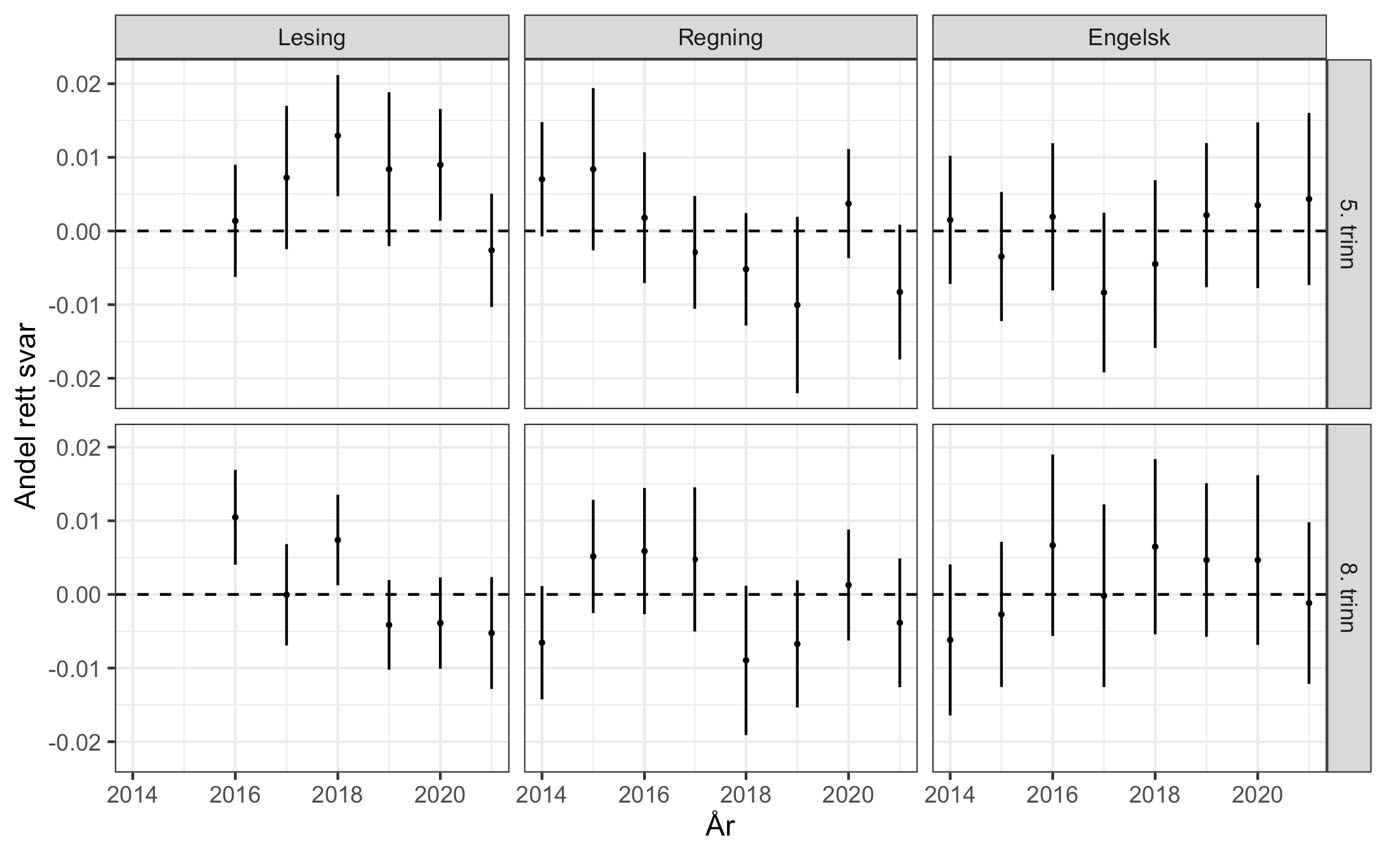
Note: De vertikale strekene for hvert trinn, år og fag viser 95 % konfidensintervall på estimert forskjell i andel riktig svar. De varierer etter fag og trinn, og dette reflekterer at det i lesing er en litt annen struktur med flere ankeroppgaver totalt sett (men ikke per elev).

Resultater – Ferdighetsutvikling over tid

Det første enkle spørsmålet vi stiller er: Oppnår ankerelevene bedre eller dårligere resultater på de samme ulike individuelle ankeroppgavene over tid? For å undersøke dette starter vi med å beregne andel med rett svar på hver enkelt ankeroppgave i hvert år og plotte hver ankeroppgaves svarandel over tid som en linje over de årene oppgaven var i bruk (figur 2). Oppgaver som har vært i bruk i mange år får derfor en lang linje, og når en oppgave tas ut av ankersettet stopper linjen opp. Figuren viser også variasjonen i oppgavenes vanskegrad som gjør det mulig å skille mellom elever på ulike kompetansenivå.

Hvordan vil så endringer over tid arte seg i en slik figur? Vi kan skille mellom to typer endringer. Hvis elevene blir bedre/dårligere over tid, forventer vi at disse linjene stiger/faller ettersom en økende eller fallende andel klarte å svare riktig. Vi kunne også fått en endring i gjennomsnittlig andel rette svar selv om elevenes ferdigheter var uendret, men dette ville i så fall skje ved at nye ankeroppgaver systematisk var lettere eller vanskeligere enn de som ble erstattet. I et slikt (tenkt) tilfelle ville hver oppgave vært en horisontal linje, og utbyttingen av oppgaver ville gi nye linjer som systematisk lå lavere eller høyere enn oppgavene de erstattet (som en trapp).

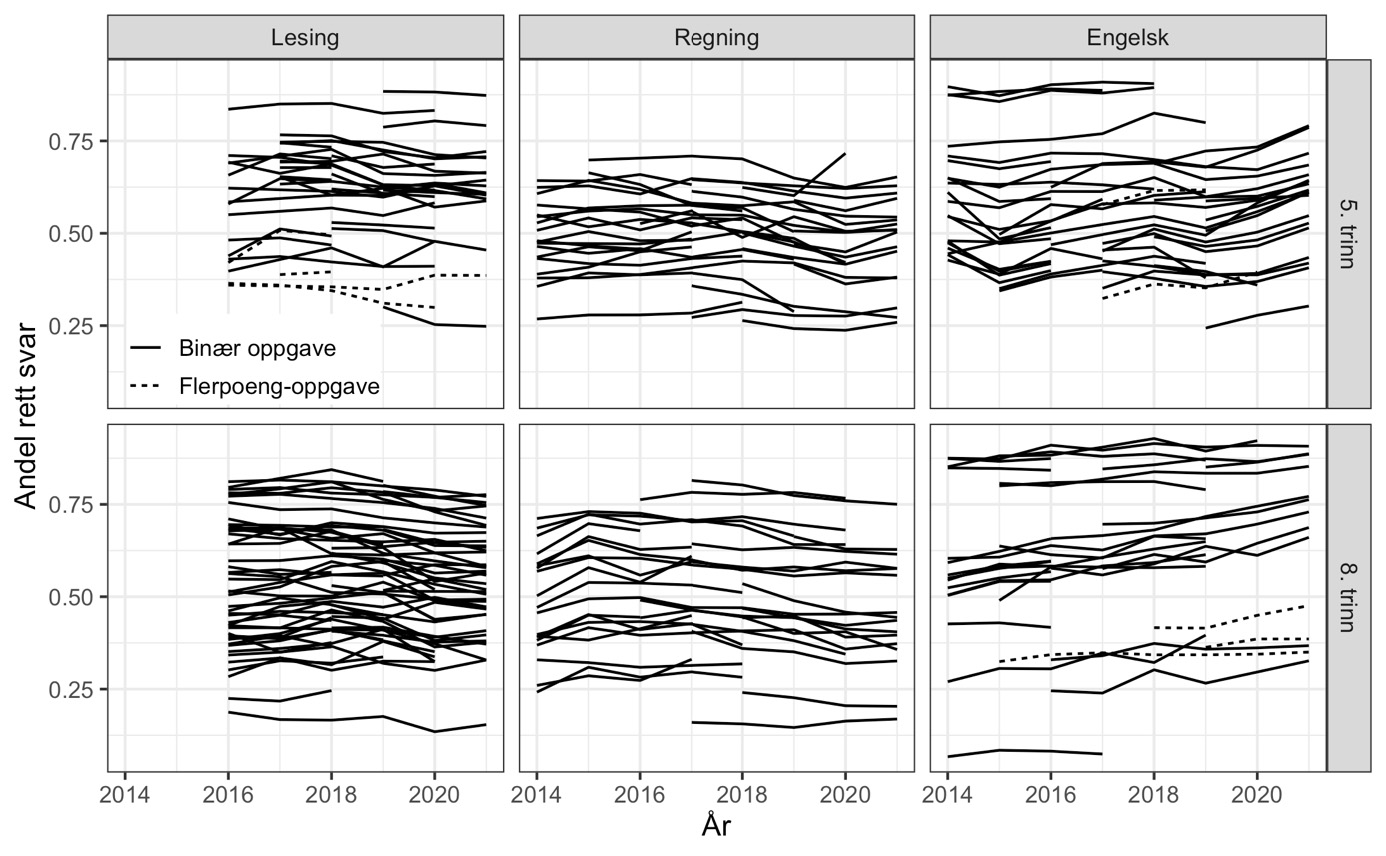
Note: Andel riktige svar for hvert år, trinn og fag. Kun ankeroppgaver. Flerpoeng-oppgaver er kodet med andel av maks oppnåelige poeng og markert med stiplet linje.

Ser vi så noe tegn til endring i figur 2? Om vi begynner nede i høyre hjørne med engelsk på 8. trinn, er det ganske tydelig at linjene peker oppover, altså at elevenes ferdigheter ser ut til å ha økt. For de andre prøvene er det ikke lett å se noen tydelige trender i denne figuren.

For å gjøre det enklere å se utviklingen over tid sentrerer vi alle linjene så de starter på null første året de er med (figur 3). Dette får tydeligere fram at ulike oppgaver over tid har fulgt en lik trend. Prestasjonene i engelsk, både for 5. trinn og for 8. trinn, har blitt betydelig bedre over tid. For lesing på 5. trinn kan vi skimte mindre endringer, mens det for 8. trinn ser ut til å være et fall de siste årene. Også for regning ser andelen riktige svar ut til å ha gått noe ned på både 5. og 8. trinn.

Det neste spørsmålet vi stiller, er hvordan sannsynligheten for korrekt svar på ankeroppgaver har endret seg – i gjennomsnitt over alle ankeroppgaver – gjennom årene fra 2014 til 2021. For å besvare det estimerer vi den sannsynlighetsmodellen i ligning (1) omtalt over med faste kohort- og oppgaveeffekter. Intuitivt sett beregner modellen tidsutviklingen i andelen med rett svar for hver oppgave separat, før den vekter disse sammen til et gjennomsnitt over ulike oppgaver. Resultatene er vist i figur 4 der den vertikale streken for hvert år indikerer et 95 % konfidensintervall rundt estimatet på års- (eller kohort-) effekten.

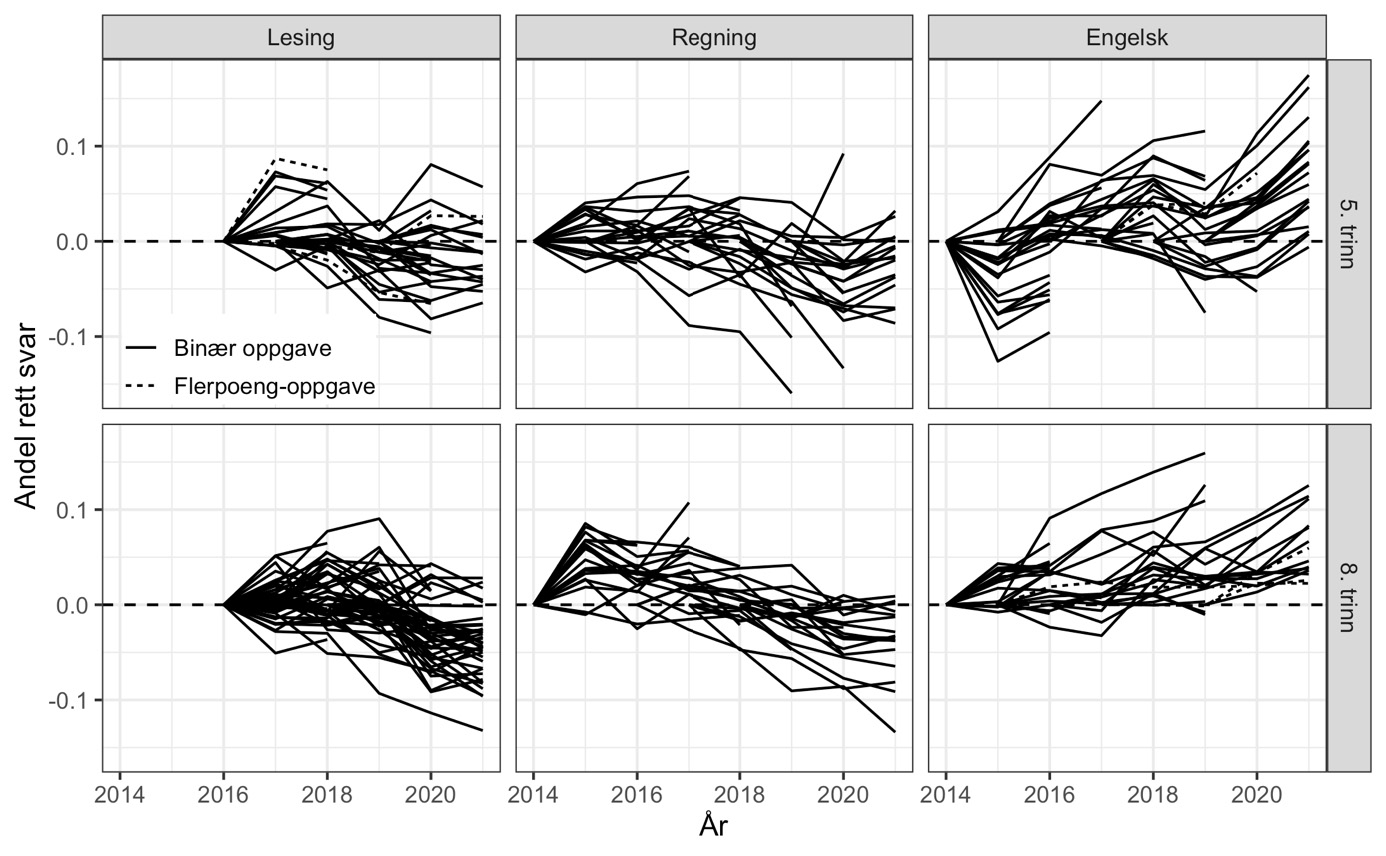
Note: Andel riktige svar for hvert år, trinn og fag er fratrukket andel riktige det først året prøvene for denne gruppen ble gjennomført. Flerpoeng-oppgaver er kodet med andel av maks oppnåelige poeng og markert med stiplet linje.

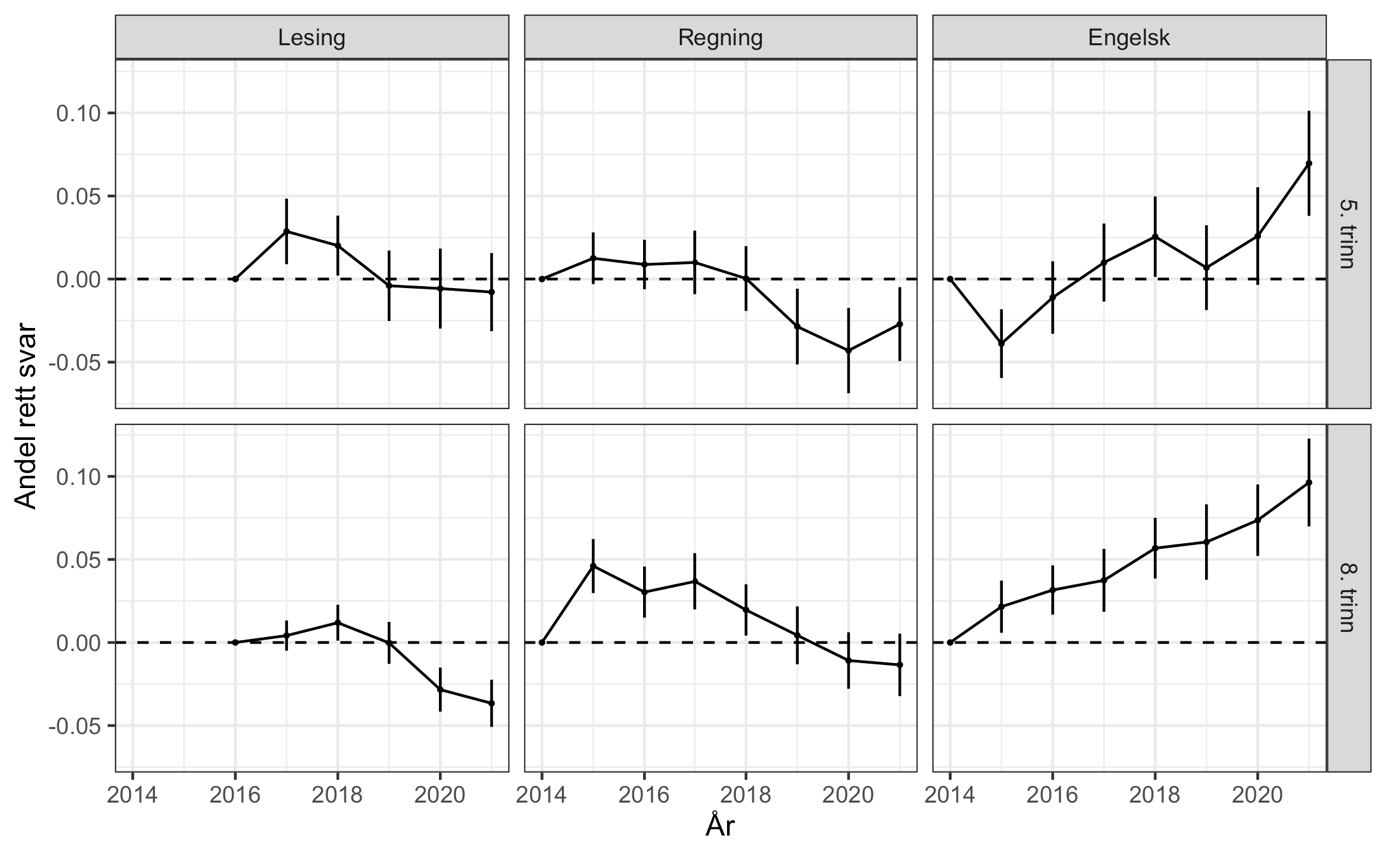
Note: De vertikale strekene for hvert trinn, år og fag viser 95 % konfidensintervall.

Mønstrene i figur 4 peker klart i samme retning som den grafiske analysen av enkeltoppgaver i figur 3. Det er klare forskjeller i hvor godt ulike års ankerelever besvarer de samme oppgavene. Merk også at forskjellene mellom fødselskull er betydelig større enn de forskjellene vi fant mellom ankerelever og «andre elever» i ulike år (figur 1). Mønstrene vi nå ser, skyldes derfor ikke at ankerelevene tilfeldigvis avviker fra resten av skolekullet sitt.

Om vi starter med engelsk på 8. trinn nederst til høyre i figuren, ser vi at andel riktige svar har økt med 0.1 (10 prosentpoeng). Fra en gjennomsnittlig andel riktige på rundt 0.57 (57 prosent) i 2014 (ikke vist i figuren), har elevene på 8. trinn altså økt andelen rette svar med 17–18 prosent! Også på 5. trinn er kompetansen i engelsk blitt mye bedre over tid. Etter et fall fra 2014 til 2015 er forbedringen jevn fra år til år.

I regning ser vi at det har vært noe nedgang for 5. trinn etter 2018, mens prestasjonene på 8. trinn først økte fra 2014 til 2015 og deretter har falt jevnt og trutt tilbake til, og forbi, 2014-nivået de siste par årene. Andelen riktige svar på ankeroppgavene i regning i 2021 er lavere på både 5. og 8. trinn enn i 2014.

I lesing ser vi at ferdighetene på 8. trinn er svekket de siste to-tre årene. Nedgangen i lesing i norsk er betydelig mindre enn forbedringen i engelsk, men utgjør likevel en nedgang på 5 prosentpoeng siden 2018.

Mønstrene i figur 4 representerer langt større endringer enn hva som kan skjule seg bak et avrundet 50 i gjennomsnittlig antall skalapoeng og burde derfor ha dukket opp i de offisielle tallene.

Utviklingen i gjennomsnittlige skalapoeng

Analysene av endringer i ankeroppgavene hviler på en forutsetning om at ankerelevene er representative for sitt kull. Innenfor IRT-rammeverket er ikke dette nødvendig, men det er viktig at ankerelever har ulike ferdighetsnivåer for å kunne sette ulike års prøver på samme skala. Analysene benytter hele oppgavesettet for alle elever innenfor en fag/trinn-kombinasjon. Resultatene fra alle analysene er konvertert til Udirs skalapoeng, der ferdighetene i referanseåret var 50 i gjennomsnitt og med et standardavvik på 10.

Våre hovedresultater er basert på lenkemetoden FCIP omtalt over og som Udir rapporterer å ha brukt for årene 2014–2021. Ved hjelp av R-pakken mirt har vi altså benyttet den samme metoden som Udir oppgir å ha benyttet. For å validere FCIP-analysene gjorde vi også lenkingen av prøvene med samkalibrering på tvers av alle år ved hjelp av funksjonen multipleGroup i mirt (Chalmers, 2012). Koder for begge metoder er gjengitt i vedlegget.

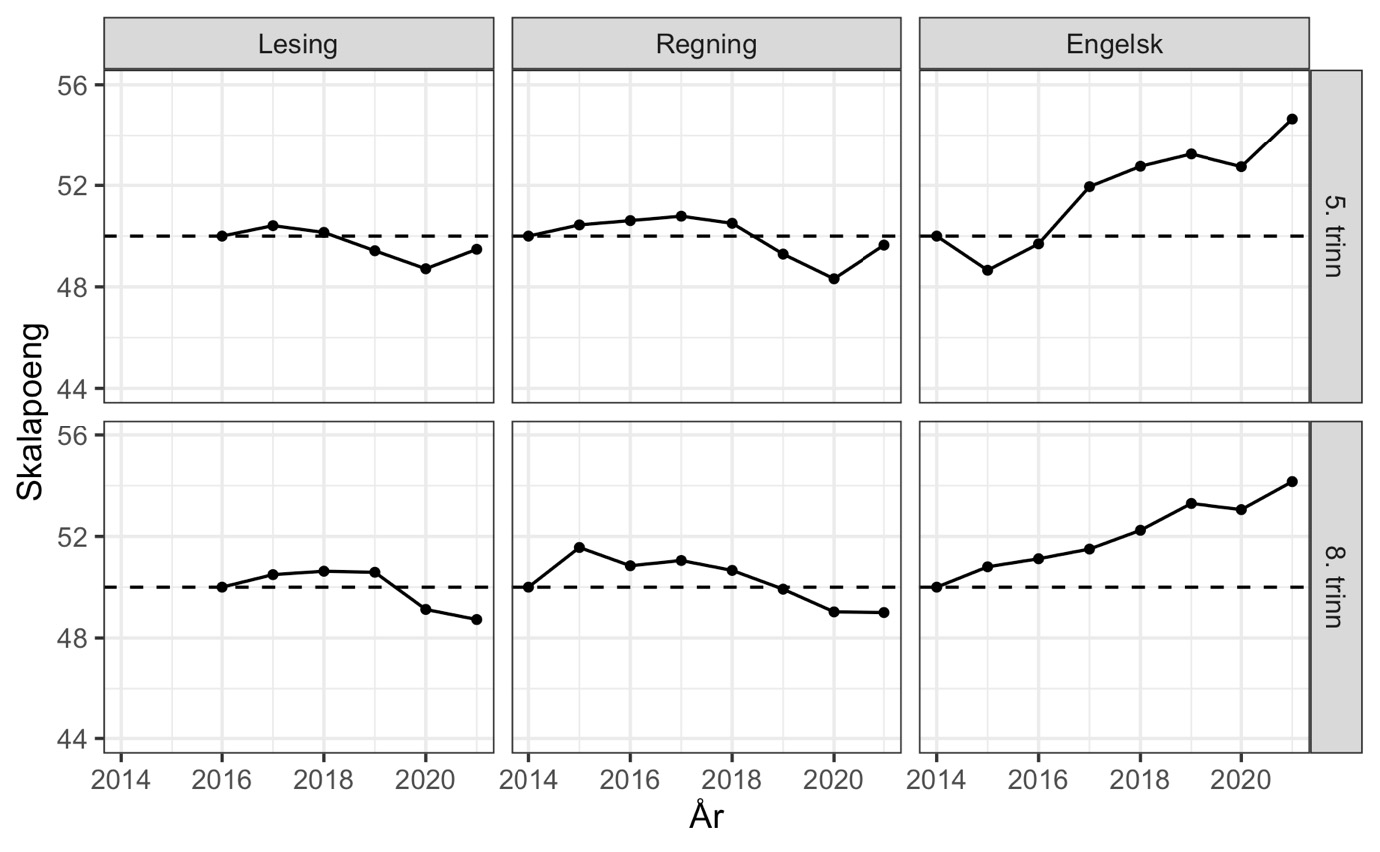
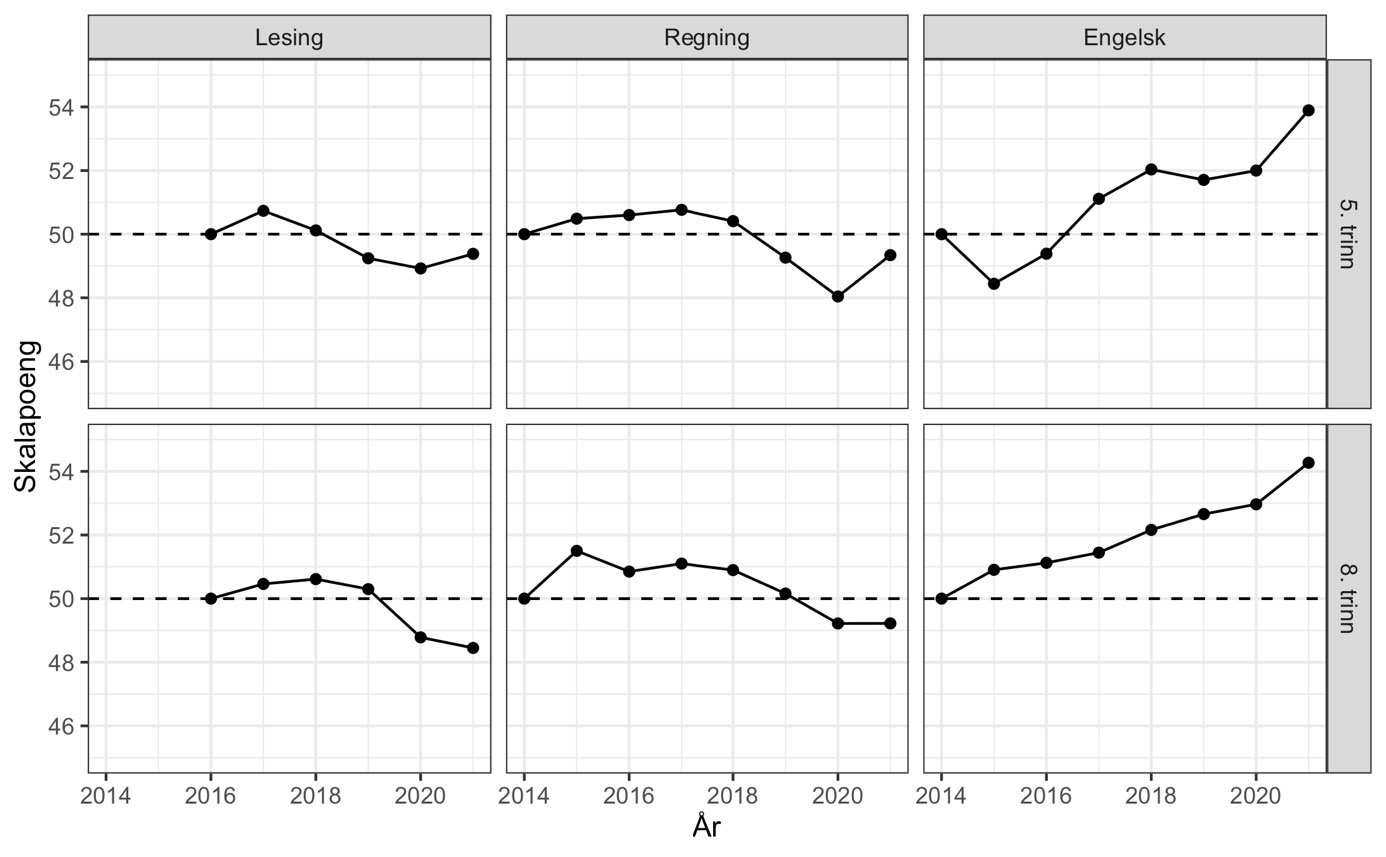
Note: Estimert med FCIP kalibrering i mirt-pakkens mirt-funksjon. Koden er beskrevet i vedlegget.

Våre anslag for utvikling i ferdigheter fra både FCIP-lenking (figur 5) og samkalibrering (se vedlegg) er slående like mønstrene vi avdekker med den lineære sannsynlighetsmodellen. Engelskkunnskapene var i 2021 langt bedre enn tidligere, med en økning på over 40 % av et standardavvik sammenliknet med 2014. Så langt vi kjenner til, finnes svært få eksempler på endringer i skolen i form av ressursinnsats eller pedagogisk innhold som fører til en så kraftig forbedring av elevenes ferdigheter. Fire skalapoeng tilsvarer forskjellen i ferdigheter mellom unge med og uten foreldre på universitets- og høgskolenivå. Vi har ingen god forklaring på nedgangen i 2020. Den er særlig overraskende for 8. trinn som jo oppnådde bedre resultater enn kullene før på 5. trinn. For lesing og regning er endringene over tid mindre, men det er tydelige tegn til svakere ferdigheter i både lesing og regning de siste årene.

På grunn av den store forskjellen i antall elever som tok kohortprøve og ankerprøve, har vi testet IRT-modellene beregnet med FCIP-lenkingen på disse prøvene hver for seg. Denne tilnærmingen omgår også utfordringer med systematisk manglende data. For hver prøve ble en IRT-modell forhåndsdefinert basert på parameterne fra FCIP-lenkingen, med unntak av populasjonsparametere. For både kohortprøvene og ankerprøvene på tvers av alle fag/trinn/år passet disse IRT-modellene godt med føyningsindikatorer under anbefalte grenser (RMSEA < 0.08 og SRMSR < 0.06; se vedlegg).

Som diskutert over kan oppgaver endre funksjon over tid, såkalt oppgavedrift. I analysene over har vi inkludert alle ankeroppgavene alle de årene de er inne. En bekymring er at resultatene våre kan være forstyrret av at vi beholder ankeroppgavene i alle år de inngår. Hvis oppgaver «pensjoneres» når de viser oppgavedrift betyr dette at de gir en potensiell skjevhet i resultatene det siste året de inngår. For å undersøke dette kjørte vi IRT-modellene på nytt der ankeroppgaver det siste året de inngikk, fikk tildelt et nytt oppgavenummer. På denne måten får ankeroppgaven ulike parametere i det siste året, og kan bidra til å identifisere relativ elevkompetanse i det enkeltåret uten å forstyrre ankringen av testene. Resultatene fra disse kjøringene ble såpass like at kurvene for tidsutvikling visuelt ikke kunne skjelnes fra hverandre.

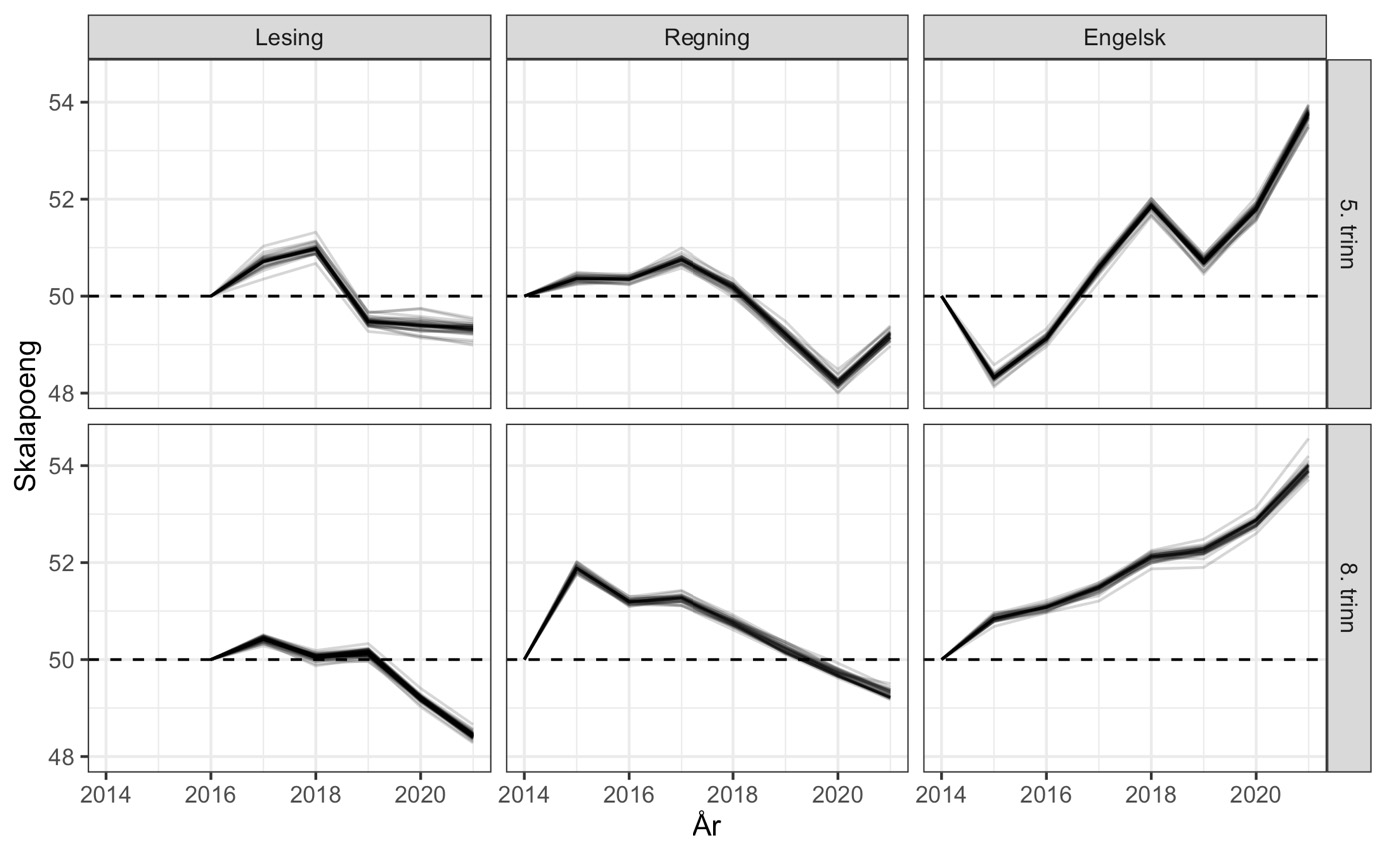
Note: Estimert med mirtMultigroup, se vedlegg.

For å ytterligere teste hvor følsomme resultatene er for enkeltoppgaver som eventuell endrer betydning, estimerer vi modellen mange ganger hvor én og én ankeroppgave utelates. I figur 6 ser vi resultatene fra en slik «simplified jackknife» strategi. For hver kjøring tegner vi en linje for gjennomsnittlig antall skalapoeng. Vi ser at endringene vi har dokumentert over er svært lite følsomme for å utelate enkeltoppgaver.

Hvor i ferdighetsfordelingene ser vi endringer over tid?

Bak et gjennomsnitt kan det skjule seg endringer i ulike deler av ferdighetsfordelingen. Fra IRT-analysen får vi anslag på kompetansen til hver enkelt elev, og når vi sorterer dem kan vi studere utviklingen for ulike persentiler (figur 7). For engelsk på 5. trinn ser vi tydelig at de beste i hvert kull har blitt enda flinkere over tid. Nesten én av fem elever i engelsk på 5. trinn oppnådde minst 65 skalapoeng i 2021, noe bare én av ti evnet i 2014. Kompetansen hos de svakeste i engelsk på 5. trinn, derimot, er mer eller mindre uendret siden 2014.

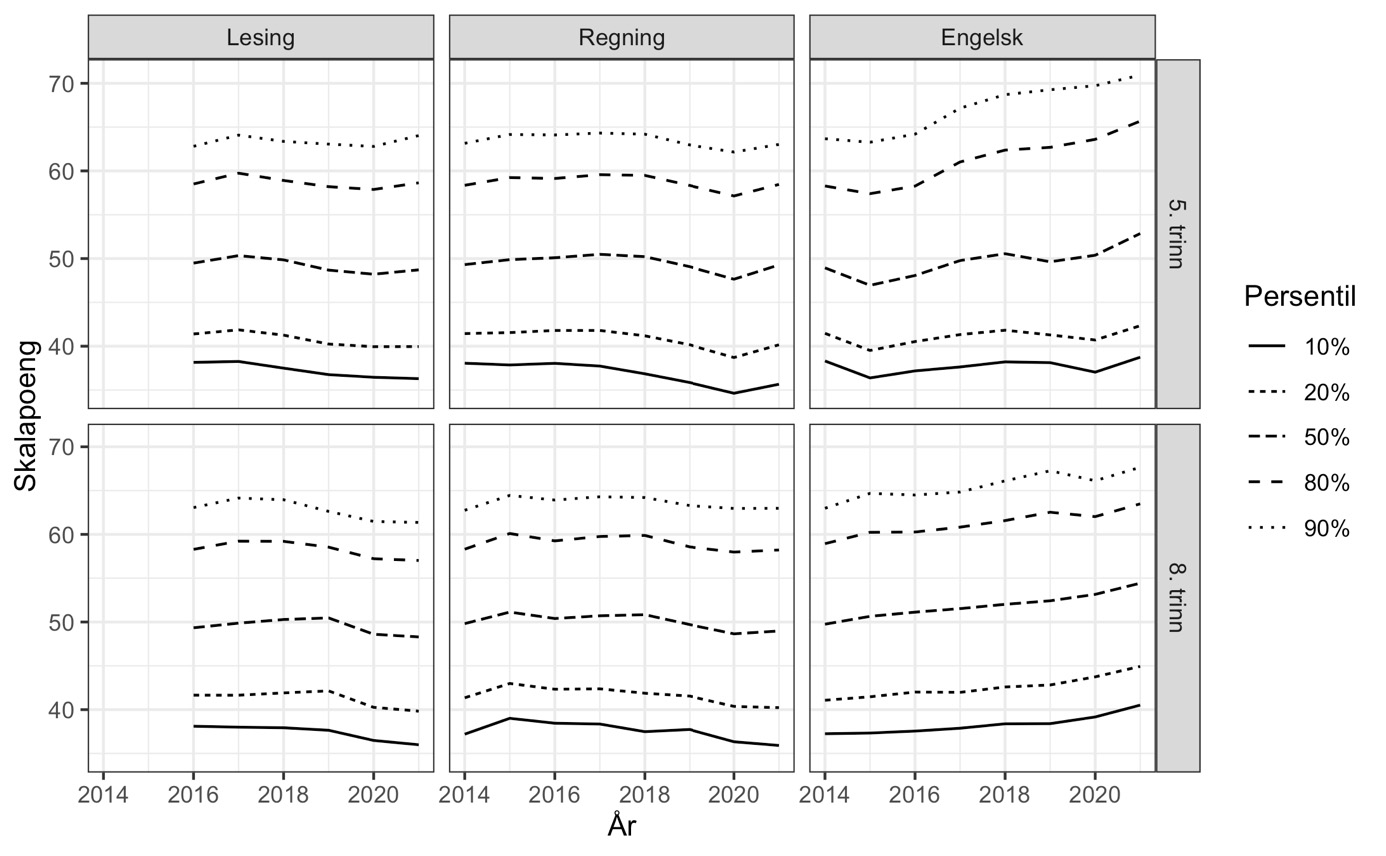
Note: Estimert med mirtMultigroup, se vedlegg.

Utviklingen for engelsk på 8. trinn er jevnere. Alle er blitt bedre i engelsk, og det er ingen åpenbar forskjell i tidsutviklingen for ulike deler av ferdighetsfordelingen.

For lesing og regning på 5. trinn er det tegn til at de 10–20 % svakeste de siste årene oppnår færre skalapoeng enn tidligere og at denne utviklingen forklarer fallet i gjennomsnittet vist i figur 5. På 8. trinn i lesing og regning viser figur 7 en parallell utvikling for alle delene av ferdighetsfordelingen.

Kjønnsforskjeller

I figur 8 viser vi utviklingen i gjennomsnittlige skalapoeng delt etter kjønn. Vi ser at utviklingen over tid har vært ganske lik for gutter og jenter i engelsk og lesing. I regning kan det se ut som om kjønnsforskjellen har økt noe de siste par årene.

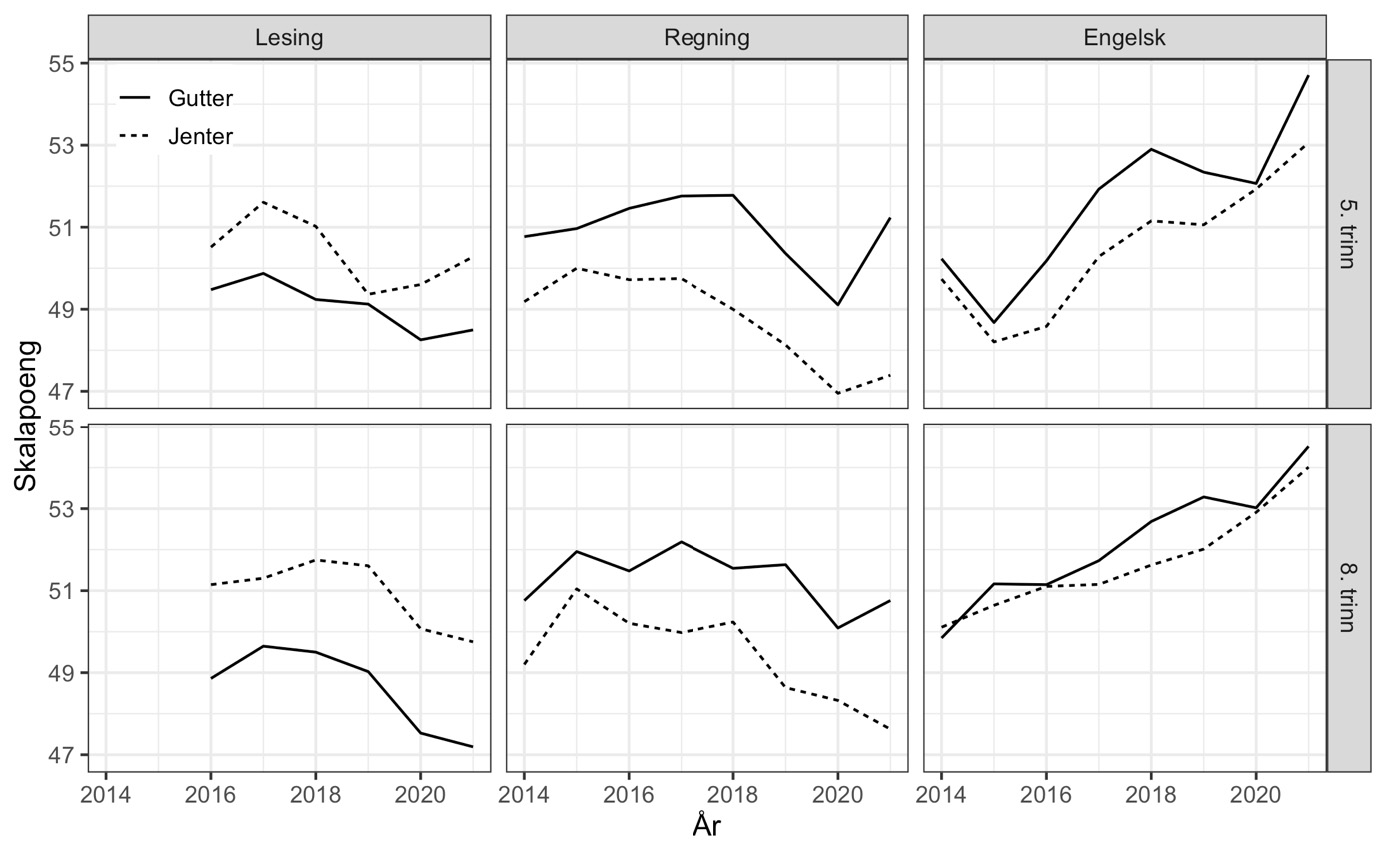
Note: Estimert med mirtMultigroup, se vedlegg.

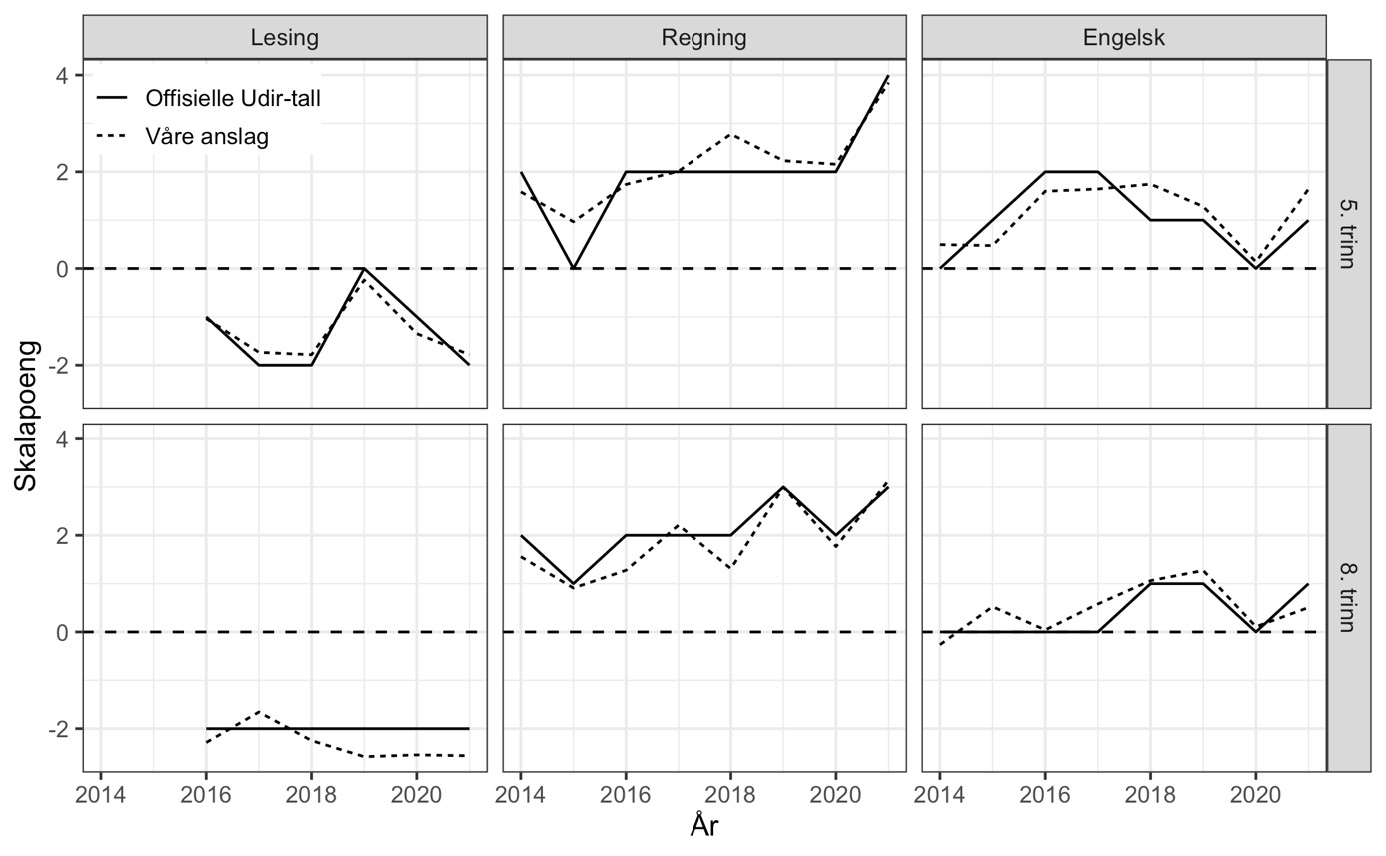
Note: Våre beregninger med mirtMultigroup, se vedlegg.

Kjønnsforskjellene gir oss også en anledning til å sammenholde våre resultater med de offisielle tallene (figur 9). Disse viser relativt stabile mønstre der jentene leser bedre enn guttene, mens guttene i gjennomsnitt har høyere regnekompetanse enn jentene. For engelsk er kjønnsforskjellen mindre, særlig på 8. trinn. I figur 9 viser vi utviklingen i forskjellen i skalapoeng mellom gutter og jenter i vår IRT-analyse, sammenliknet med Udirs publiserte (avrundede) tall. I all hovedsak viser de to seriene det samme bildet.

Hva gikk galt?

De offisielle tallene er basert på IRT-modeller estimert i programvaren XCalibre. Med dokumentasjonsmateriale fra Udir og gratislisenser fra XCalibre har vi reprodusert de offisielle tallene for regning. Feilen ligger altså ikke på brukersiden. De riktige rådataene ble analysert og programvaren ble brukt i henhold til brukerhåndboken.

Dermed står vi overfor to analysetilnærminger med svært ulike svar. Representerer de alternative og likestilte rammeverk der begge har støtte i faglitteraturen? Eller kan vi konkludere at en av dem er feil? For å avgjøre hvilken tilnærming som er korrekt, sammenlikner vi de to på et datamateriale der fasiten er kjent: 100 uavhengige syntetiske datasett der vi selv velger den sanne ferdighetsfordelingen. Hvert syntetiske datasett ble konstruert på samme måte: 10 000 elever fra hver av to grupper fikk trukket sine faktiske ferdigheter (theta-verdier). Mens elevene i gruppe 1 ble tilfeldig trukket fra en N(0,1) fordeling, ble elevene i gruppe 2 trukket fra en N(0.5, 1.2) fordeling. Målt på skalaen fra gruppe 1 ligger altså gruppe 2 nøyaktig 0.5 høyere i snitt. Oppgaveparametere ble trukket for 2x50 gruppe-spesifikke oppgaver og 20 ankeroppgaver. I hver gruppe ble 1000 elever trukket tilfeldig til å være ankerelever. Sannsynligheten for riktig svar på en oppgave er nå gitt av elevens theta og oppgavens parametere, jf. ligning (2). For hver elev ble så svar på enkeltoppgaver trukket ut fra denne sannsynligheten. Dette ga oss 100 datasett der vi vet hva forventet ferdighet og standardavvik (populasjonsparametere) faktisk er for hver av de to gruppene. Hvert datasett ble estimert med fire ulike metoder:

1. XCalibre: Udirs metode med FCIP der ankeroppgaver i gruppe 2 får parameterverdier anslått fra gruppe 1.
2. mirt fixed par: En «kopi» av av Udirs metode estimert med mirt FCIP der elevene i begge gruppene antas å komme fra den samme ferdighetsfordelingen N(0,1).
3. mirt free par: Modellen brukt for våre hovedresultater, også implementert med mirt FCIP, men der forventning og standardavvik i gruppe 2 estimeres fritt.
4. multipleGroup: Simultan samkalibrering der gruppene er fristilt og kan ha ulike snitt og varians, men der parameterne for ankeroppgaver antas å være like i begge grupper.

Det kritiske spørsmålet er om metodene avdekker den store faktiske forskjellen mellom gruppene. Et enkelt mål på dette er å dele anslaget fra hver kjøring på den sanne verdien. Dess bedre resultatet treffer, dess nærmere 1 vil denne brøken ligge. I figur 10 viser vi variasjonen i brøken for hver metode over de 100 simulerte datasettene ved hjelp av et «fiolinplott». Boblen i fiolinplottet viser fordelingens tetthet og rektangelet i midten går fra første til tredje kvartil med en indre strek som angir medianverdien. Vertikale streker på hver side av rektangelet angir spredningen i de ytterste kvartilene – mens prikker utenfor rektangelet illustrerer ekstremverdier på mer enn 1.5 av kvartilverdien. Den stiplede linjen angir korrekt estimat.

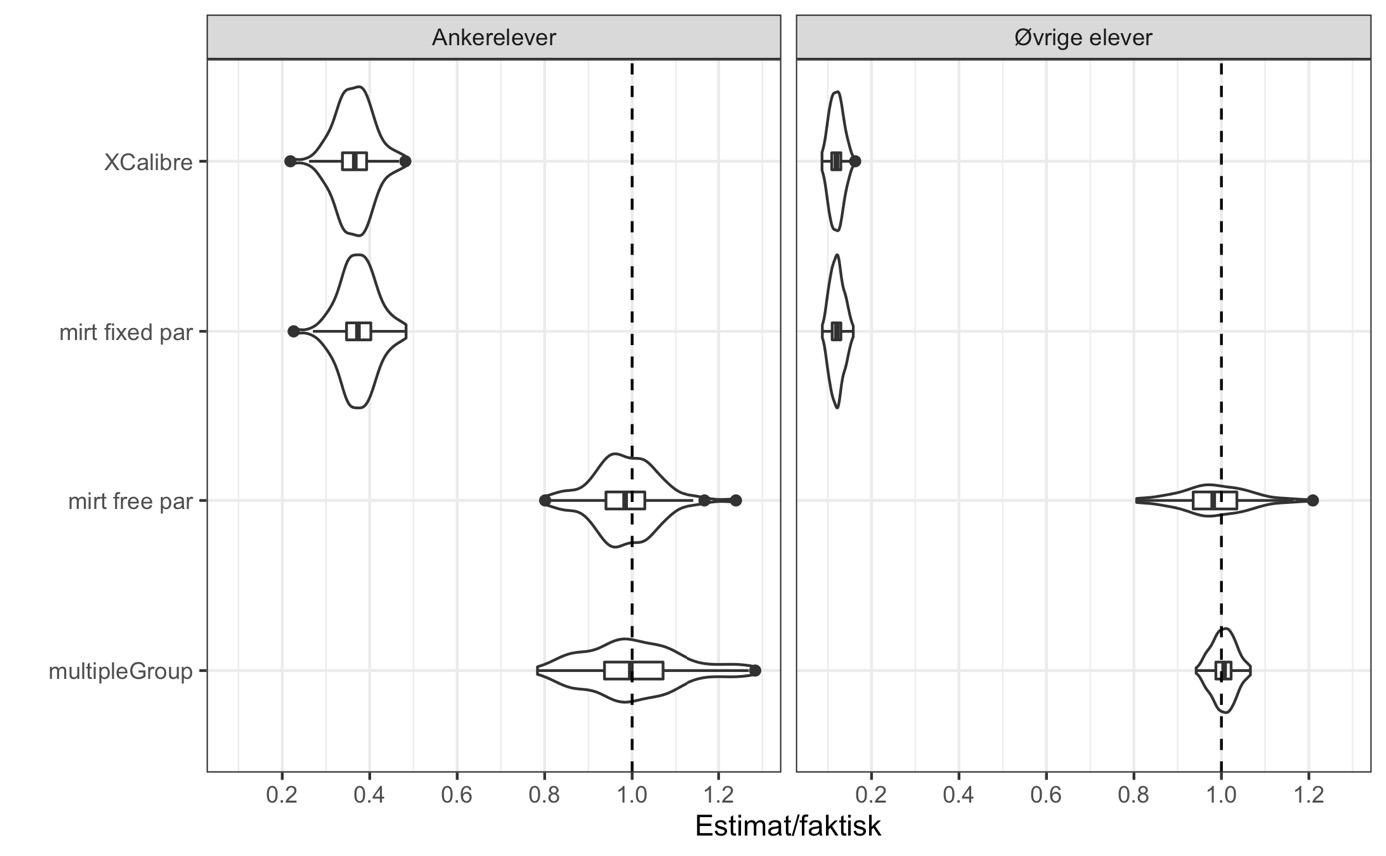
Note: Fire estimeringsmetoder ble implementert på hvert av 100 syntetiske datasett der den sanne forskjellen mellom to grupper var kjent. Figuren viser hvordan anslaget lå i forhold til sannheten over de 100 kjøringene. Den stiplede linjen markerer «perfekte» estimat. Hvert datasett inneholdt simulerte prøvesvar fra 10 000 «elever» i hver gruppe, hvorav hver tiende elev var ankerelev. Simulerte prøver hadde 50 årsspesifikke oppgaver, ankerelever fikk byttet ut 20 av oppgavene med ankersettet.

Resultatene er både entydige og slående. For det første blir det faktiske nivået i gruppe 2 presist estimert enten man bruker multipleGroup eller mirt FCIP med fristilte populasjons-parametere. For det andre har programvaren som har blitt brukt historisk (XCalibre), en kraftig skjevhet mot null. For ankerelevene ligger brøken rundt 0.4, men skjevheten er langt mer alvorlig for de øvrige elevene med en brøk omkring 0.1. For det tredje finner vi den samme sterke skjevheten mot null dersom vi bruker mirt men legger til grunn at populasjonsparameterne er kjent (mirt fixed par). Over de 100 simuleringene har XCalibre og denne feilspesifiserte mirt-modellen en korrelasjon på 0.995.

Dette siste gjør at vi kan konkludere med at XCalibre ikke kan brukes for å implementere et FCIP-design der formålet er å plassere elever fra ulike år på samme ferdighetsskala. De publiserte norske tallene er basert på en analyse som legger til grunn at elever fra ulike år (forventningsmessig) er like, noe som gjør at de faktiske endringene som har skjedd har blitt underestimert så kraftig at de ikke lenger var synlige etter at Udir avrundet årssnitt til hele skalapoeng.

Diskusjon

Er våre anslag på utviklinger i elevers ferdigheter overraskende? Vi mener ikke det. For engelsk annetspråk finnes så vidt vi vet ingen internasjonale studier av kunnskaper blant barn og unge over tid, men våre resultater sammenfaller med budskapet fra lærere og språkforskere (samt våre egne personlige erfaringer): unges engelskkunnskaper har blitt kraftig forbedret gjennom økt eksponering for engelsk på ulike spill- og medieplattformer. Således er det ikke overraskende at norske barn og ungdom behersker engelsk langt bedre enn de likealdrende gjorde for syv år siden. For lesing og regning er våre funn grovt sett på linje med mønstre i PISA og TIMSS fra 2015/2016 via 2018 og fram til 2022. Når PIRLS viser en betydelig svekkelse av 10-åringers leseferdigheter fra 2016 til 2021 og PISA-ferdigheter faller fra 2018 til 2022 i alle fag, er mønstrene helt i tråd med våre beregninger fra de nasjonale prøvene.

De nasjonale prøvene er en viktig del av kvalitetssikringen av norsk skole (NOU 2023:1). Det er viktig for både myndigheter, skoleeiere, elever, lærere og andre med interesse for norsk skole å vite hvordan kunnskapsnivået for norske barn og ungdom utvikler seg. Samtidig er mange skeptiske til hva prøvene krever av tid, hva de måler og hvordan de kan bidra til (uønsket) endring i læringsfokus i retning av målbare kompetanser.

Utdanningsdirektoratet konkluderer at «Nasjonalt er det ingen endring i gjennomsnittlig skalapoeng i lesing, regning og engelsk fra vi startet å måle utviklingen over tid og frem til 2021» (Udir, 2021).

Ekspertgruppen «Utvalget for kvalitetsutvikling i skolen» (NOU 2023:1) virker ikke overrasket og uttrykker forventning om høy stabilitet: «Det tar likevel mange år før det er mulig å se eventuelle endringer i trender, spesielt hvis det er mange i utvalget. Nesten alle elevene på hvert årskull, det vil si om lag 60 000 elever, gjennomfører de nasjonale prøvene på 5., 8. og 9. trinn hvert år. Gjennomsnittet i en såpass stor utvalgspopulasjon er stort sett stabilt, og det skal store endringer til før disse blir synlige i det nasjonale gjennomsnittstallet» (s. 83–84). Dersom Udirs konklusjon og ekspertgruppens påstand om at «det skal store endringer til før disse blir synlige» er riktige, vil en naturlig kunne hevde at verktøyet med nasjonale prøver er lite egnet for å måle ferdighetsutvikling over tid.

Særlig hvis måleinstrumentet var så lite nøyaktig at det ikke fanget opp utviklingstrekk vi fant i andre kilder. Men begge premissene er feil. Våre resultater viser derimot at de nasjonale prøvene er svært godt egnet til dette formålet. Systemet kan avdekke viktige endringer over tid i både gjennomsnittsnivå og forskjeller innad i elevmassen. Til forskjell fra de internasjonale studiene gir de nasjonale prøvene år-til-år-informasjon om utviklingen i ferdigheter. Våre beregninger viser klare indikasjoner på fall i leseferdigheter de senere årene i god tid før PIRLS 2021 dokumenterte et kraftig fall mellom 2016 og 2021. Slike endringer er potensielt viktige for utformingen av skolepolitikken, enten det er for skoleeier lokalt eller på sentralt nivå. La oss nevne kun ett eksempel. Skoledagen har et gitt antall timer, men det er ikke opplagt hva de skal brukes til. Flere timer i ett fag går på bekostning av andre. Hvis elevene lærer mye på andre arenaer enn skolen, kan det argumenteres for at dette også bør føre til endring i timefordelingen i skolen. Når det argumenteres for mer fysisk aktivitet i skolen, er gjerne noe av bakteppet at mange elever er (mer) stillesittende på fritida (enn tidligere). Om elevene lærer mer engelsk på fritida og oppnår vesentlig høyere ferdigheter, kan det være et argument for å vri litt av tidsbruken fra engelsk til for eksempel lesing og regning der vi ser tegn til at de svakeste sliter mer enn før.

Etter vår vurdering bør funnene også få konsekvenser for hvordan resultater fra nasjonale prøver presenteres, analyseres og gjøres tilgjengelige for forskning med personvernhensyn godt ivaretatt. Enklere og mer gjennomsiktige analyser av resultatene – i tillegg til komplisert modellering av latente ferdigheter – vil gjøre det mulig for utenforstående miljøer å delta i en faglig debatt om metoder og utviklingstrekk. Det bør også være en selvfølge at Udir fortsetter å dele både data og koder for analyser av data med interesserte. En slik åpenhet vil bidra til at prøvesvarene blir tolket riktig. Udirs valg om å bytte analyseplattform fra en kommersiell og dyr programvare til en programpakke som er utviklet av akademikere og gjort fritt tilgjengelig («mirt»-pakken i R) er et godt steg i den retningen, og vil også gjøre det enklere å dele estimerings-spesifikasjoner og lettere avdekke årsakene til at ulike miljø kommer til forskjellige resultater med det samme datamaterialet.

Oppgavedata bør gjøres lett tilgjengelig for forskning. De bør tilrettelegges for andre enn Udir og deres samarbeidspartnere, i en form som tillater kobling av besvarelser mot andre registerdata. Dataene vi har analysert i denne artikkelen, er fullstendig anonyme og uten muligheter for å identifisere hvem elevene er, hvilke skoler de går på eller hvem som går på skole sammen. Tilbakemeldingen vi har fått fra Udir er at alle koblbare data på individnivå er slettet og at vi må henvende oss til skoleeier, altså hver enkelt kommune, for å be om tilgang til slike data. Alle forstår at for én enkelt forskningsgruppe representerer det å innhente tillatelse til å koble mikrodata fra over 300 kommuner en nær uoverkommelig oppgave. Vi har vanskelig for å se tungtveiende grunner til at slike oppgavedata skal slettes/ anonymiseres i større grad enn annen informasjon som i dag lagres som personopplysninger i ulike offentlige registre og lånes ut til forskning i et stort omfang.

Konklusjon

Nasjonale prøver er utformet på en måte som muliggjør sammenlikninger av elevenes ferdigheter over tid ved at tilfeldig utvalgte elever får samme oppgaver flere år på rad. De offisielle tallene sier at fagkompetansen – målt på en fast skala – har vært fullstendig stabil i både lesing, regning og engelsk på både 5. og 8. trinn.

Vår studie benytter anonymiserte data for alle besvarelsene på oppgavenivå. Dette gjør det mulig å beregne utviklingen over tid ved hjelp av ulike metodiske tilnærminger. Data som vanligvis lånes ut til forskere via Statistisk Sentralbyrå, er samlemål i form av skalapoeng og mestringsnivåer som allerede er bearbeidet og kalibrert av Utdanningsdirektoratet.

Vi har analysert tidsutviklingen i resultater fra enkeltoppgaver i de nasjonale prøvene, både grafisk og ved hjelp av ulike statistiske metoder. På tvers av disse er våre funn konsistente: Det har vært en klar trend med økt kompetanse i engelsk fra 2014 til 2021, mens ferdighetene i lesing og regning har blitt noe svakere de fire-fem siste årene. Våre anslag for engelsk viser en økning på hele 4 skalapoeng siden 2014 for både 5. og 8. trinn. Dette er en økning på 40 % av et standardavvik og tilsier at en gjennomsnittselev fra 2021 ville skåret bedre i engelsk enn 65 % av elevene i 2014. For engelsk på 5. trinn er det elevene som behersker engelsk godt, som har blitt enda flinkere over tid. På 8. trinn har både relativt svake og relativt sterke elever økt sine engelskferdigheter.

Våre anslag på tidsutviklingen og de offisielle tallene er ikke likeverdige tolkninger av data. Det er feil å forklare forskjellene med ulike metoder basert på velbegrunnede antakelser. Omfattende analyser av simulerte data der sannheten er kjent, viser utvetydig at de offisielle tallene er misvisende. Programvaren Udir benyttet i perioden 2014–2021 la til grunn at elevene i ulike år alle var trukket fra den samme uendrede ferdighetsfordelingen. Dette er ikke forenlig med intensjonen om å måle endringer over tid og må anses som en feilspesifisering av modellen – gitt hva som var hensikten. Konsekvensen var at forskjellene over tid dermed ble «krympet» i en grad som gjorde dem usynlige etter avrunding til hele skalapoeng. Det er kun for engelsk på 5. trinn i 2021 – der våre anslag viser et elevsnitt på 54.7 – at resultatene var så gode at de ble rundet opp til 51 i Udirs krympede tall.

I sum betyr dette at de offisielle tallene bør anses som utvetydig feil – de er uegnet til å vise endringer over tid og mangler støtte i både faglitteratur og god praksis. I skrivende stund er vi i dialog med både Udir og Statistisk Sentralbyrå for å lage korrekte skalapoeng på elevnivå for perioden 2014–2021, for bruk både i offisiell statistikk og i forskning basert på individdata. Dersom elevenes ferdigheter har endret seg systematisk over tid reiser dette et spørsmål om årsaker. Her er det flere mulige forklaringer som framtidig forskning bør forsøke å teste, for eksempel (i) Har elevsammensetningen endret seg på en måte som kan forklare dette? (ii) Har skolen blitt bedre/dårligere til å utvikle elevenes ferdigheter? (iii) Har elevenes relative tidsbruk på aktiviteter som utvikler ulike ferdigheter endret seg over tid? Eksempel: Er det fordi elevene bruker mer tid på teknologi og medier at de får både styrkede engelskferdigheter og dårligere evne til å lese og forstå tekst?

Både for innsikt i ulikhetsskapende forhold og for valg av mulige tiltak i skolen, bør det gjennomføres systematiske analyser av hvilke elevgrupper som endrer ferdigheter mest/minst over tid. Slike studier bør vektlegge forskjeller ut fra kjønn, sosial bakgrunn og hvor elevene befinner seg i ferdighetsfordelingen.

Våre funn sår ikke tvil om nytten av de nasjonale prøvene. Tvert imot avdekker vi interessante mønstre som er viktige for utformingen av – og prioriteringene i – norsk skole.

Vedlegg

Tabell V1. Variasjonsbredde til indikatorer for hvor godt modellene passer data for kohort- og ankerprøver

Note: Estimerte populasjonsparametere for elevferdigheter estimert med funksjonen multipleGroup i mirt-pakken.

Lineær fast effekt OLS i R Installer og last inn pakken "fixest":

Install.packages("fixest")

Library(fixest)

Modellen kjøres med kommandoen:

temp <- feols(I(value/item_max) ~ factor(year) | question,

cluster = c("id",

"question"),

data = data_inn)

Data (her kalt data_inn) er en data.frame som inneholder en observasjon for hver poengskår hver ankerelev har fått på en besvart ankeroppgave. Datasettet dekker alle ankeroppgaver (definert som oppgaver som brukes i mer enn 2 år) og alle ankerelever (definert som elever som svarer på mer enn 5 ankeroppgaver). Estimeringen bruker følgende variabler:

• Value: skår på oppgaven
• Item_max: høyeste oppnåelige skår på oppgaven (dvs. 1 for dikotome oppgaver og >1 for polytome)
• Year: testkullet til eleven
• Question: oppgave-nummeret (som unikt identifiserer oppgaven på tvers av år, samme som kolonnenavn i datamatrisen i IRT-estimeringen)
• Id: elev-ident. Datasettet er anonymt, så dette er det samme som rad-nummeret i datasettet som inngår i en IRT-analyse

Modellen er spesifisert som følger:

• Utfallsvariabelen er andel av maks poengskår (for dikotome oppgaver enten 0 eller 1)
• Det er to forklaringsvariabler
  • Year – testår angitt som faktor-variabel, det vil si omgjort til et sett med dummy-variabler
  • Question er angitt som en fast effekt (som er ekvivalent med å lage et dummysett der hver ankeroppgave får sin egen dummy-variabel)
• Vi clustrer standardfeil på individ og oppgave gjennom cluster-argumentet

Representativitet av ankerelever – analyse i R

Her bruker vi pakken "fixest" som i Fast effekt OLS analysen. Når pakken er installert og lastet ned kjøres analysen med kommandoen

Temp <- feols(I(value/item_max)~ anchor_pupil | question,

cluster = c("id", "question"),

data = data_inn)

Denne analysen bruker et datasett med informasjon om

• alle oppgaver
• i et enkelt år
• for et enkelt fag
• på et enkelt klassetrinn som er
• besvart av både ankerelever og andre.

Hver linje i datasettet inneholder skår på en bestemt oppgave for en bestemt elev. Vi bruker følgende variabler:

• Value: skår på oppgaven
• Item_max: høyeste oppnåelige skår på oppgaven (dvs. 1 for dikotome oppgaver og >1 for polytome)
• Anchor_pupil: en dummy-variabel som angir om en elev er å anse som en ankerelev. Ankerelever er definert som personer som – i et datasett med alle elever i alle testkull – har besvart mer enn fem ankeroppgaver, der ankeroppgaver er definert som oppgaver som inngår i mer enn to testår.
• Year: testkullet til eleven

Mirt koder

mirt er en pakke som kan installeres i det statistiske analyseprogrammet R.

Pakker som brukes i funksjonen er mirt for IRT-analyser og dplyr for datahåndtering. Disse pakkene kan installeres ved hjelp av kommandoene:

install.packages("mirt") install.packages("dplyr")

Når pakkene er installert kan de lastes inn i en aktiv analyse-sesjon gjennom kommandoen: library(dplyr)

library(mirt)

FCIP

For å koble resultater på en ny prøve til skalaen for en tidligere prøve kan man bruke funksjonen under. Det er nødvendig at det er et overlapp i hvilke oppgaver som ble gitt i den tidligere prøven og den nye prøven. Disse oppgavene må ha samme navn. Oppgaver som er forskjellige må ha ulike navn.

### FCIP

### ref_model is a single-group mirt model from the previous year FCIP <- function(ref_model, new_data, item_type = "2PL"){

### 1. Parameters from reference year ref_params_df <- mod2values(ref_model)

### 2. Sets estimation to FALSE for parameters from reference year ref_params_df$est <- F

### 3. Parameter structure for IRT model fitted to new_data

new_params_structure <- mirt(new_data,

1,

itemtype = item_type,

pars = "values")

new_params_order <- colnames(new_params_structure)

### 4. Replacing anchor item parameters with estimates from ref_model

new_params <- left_join(new_params_structure,

ref_params_df[c("item", "name", "value", "est")],

by = c("item", "name"))

new_params$value <- coalesce(new_params$value.y, new_params$value.x)

### 5. Setting estimation to FALSE for parameters for the items used in previous year new_params$est <- coalesce(new_params$est.y, new_params$est.x)

### 6. Restructuring parameter dataframe to comply with mirt new_params <- new_params[new_params_order]

### 7. Unconstraining population parameters (two last parameters in parameter dataframe) new_params$est[(length(new_params$est)-1):length(new_params$est)] <- TRUE

### 8. Estimating single group model with anchor item parameters fixed to values from ref_model

new_model <- mirt(new_data,

1,

technical = list(NCYCLES = 1000),

itemtype = item_type,

pars = new_params) return(new_model)

}

Funksjonen gjør følgende:

1. Henter ut en parametermatrise fra IRT-modellen fra det forrige året. Denne matrisen inneholder de estimerte oppgaveparameterne (med mirt sin parametrisering).
2. Endrer alle estimeringsinstruksene i denne matrisen til FALSE.
3. Genererer parametermatrisen som mirt vil bruke for den nye dataen.
4. Bytter ut oppgaveparameterne i den nye parametermatrisen med de estimerte oppgaveparameterne fra IRT-modellen fra det forrige året.
5. Endrer estimeringsinstruksen for ankeroppgaveparameterne til FALSE.
6. Restrukturerer den nye parametermatrisen så den har formen mirt-funksjonen krever.
7. Setter estimeringsinstruksen til populasjonsparametere til TRUE.
8. Beregner en IRT-modell basert på ny data ankret på samme skala som den forrige IRT-modellen.

Funksjonen FCIP returnerer en IRT-modell for den nye prøven på skalaen til den forrige prøven. Se dokumentasjonen til mirt, dplyr og base R for mer informasjon om funksjonene benyttet. Data som inngår:

ref_model:

• en enkeltgruppe IRT-modell estimert med mirt for det forrige året.

new_data:

• en datamatrise med data fra året som skal kobles til skalaen fra tidligere år. Dataene må struktureres så det er en rad for hver elev og en kolonne for hver oppgave fra det nye året.

item_type:

• Funksjonen antar at oppgavene kommer til å være binære (her: rett/galt kodet som 1/0) og skal beskrives med en 2PL modell. Hvis det er flerpoengs oppgaver, må en item_type settes lik en vektor som spesifiserer hvilke oppgaver som skal beskrives med hvilken IRT-modell. En slik vektor kan lages med følgende funksjon:

### Item type identifier

item_classifier <- function(new_data){

item_type <- apply(new_data, 2, max, na.rm = T)

indices_dich <- which(item_type == 1)

indices_poly <- which(item_type > 1) item_type[indices_dich] <- "2PL"

item_type[indices_poly] <- "graded"

return(item_type)

}

Hvilken IRT-modell som er ønskelig kan modifiseres ved å endre "2PL" for binære oppgaver og "graded" for polytome oppgaver. Se mirt sin dokumentasjon for alternativer og tilhørende argument.

item_classifier funksjonen trenger en datamatrise som inkluderer antall poeng oppnådd per oppgave i heltall per elev, og at binære oppgaver er kodet 1/0. Det er nødvendig at "missing data" er kodet som NA.

Multigroup (samkalibrering)

For å estimere en IRT-modell med felles skala for alle årgangene samlet i et bestemt fag og på et bestemt trinn brukte vi følgende kommando:

mirt_model <- multipleGroup (irt_data,

group = paste0("skolekull ", group_used),

technical = list(NCYCLES = 5000),

itemtype = item_type_involved,

invariance = c(constant_items,

"free_means", "free_var"))

Data som inngår:

• irt_data: en datamatrise med en rad for hver elev og en kolonne for hver oppgave som inngår i minst ett år, der oppgaver en elev ikke ble stilt er angitt som missing (NA)
• group_used: en vektor som angir test-kullet til hver enkelt elev, som her limes sammen med tekstrengen "skolekull" så gruppevariabelen blir f.eks. "skolekull 2015" for elever som tok prøven i 2015
• item_type_involved: en vektor som har en verdi for hver oppgave (kolonne) som angir hva slags oppgave det er snakk om:
  • binær eller dikotom variabel (her: rett/galt kodet som 1/0) er angitt med "2PL" som angir at vi ønsker en to-parameter IRT-modell for denne oppgaven
  • polytom oppgave, der data angir hvor mange poeng av et maks-skår større enn 1 hver elev har på denne oppgaven. Her ønsker vi modellen "gpcm".
• constant_items: en vektor med kolonner som har samme parameter på tvers av de ulike gruppene i data. Her angir vi alle anker-oppgaver, som vi har definert som oppgaver som inngår i mer enn 2 år.

I tillegg er det gjort visse spesifikasjoner i modellen:

• NCYCLES er antallet runder modellens maximum-likehood algoritme kjører før den gir opp dersom ikke konvergenskriteriet er nådd. Modellene vi kjører her er store og krevende, og antallet maks-iterasjoner måtte økes betydelig over default-nivået på 500 for at løsningen på modellen skulle bli estimert.
• "free_means" og "free_var" – dette forteller modellen at både snittet og spredningen på elevenes fagkompetanse kan være ulik for ulike testkull.