Etterutdanning gjennom å øve sammen

Etterutdanning av matematikklærere bør ha som mål å utvikle læreres kapasitet til å observere, analysere og respondere på elevers matematiske tenkning. Dette var anbefalingen etter en gjennomgang av internasjonal forskning på etterutdanning av matematikklærere gjennomført av den amerikanske forskeren Lynn T. Goldsmith og hennes kollegaer i 2014. I etterutdannings- og forskningsprosjektet som er utgangspunkt for denne artikkelen, Mestre Ambisiøs Matematikkundervisning (MAM), var målet en undervisning hvor en har satt ambisiøse mål for elevenes læring av matematikk, og hvor en arbeider seg fram mot målene gjennom å fremme dybdeforståelse hos elevene (f.eks. Lampert et al., 2013). Om en leser kjerneelementene og mål for matematikkfaget i Fagfornyelsen (Utdanningsdirektoratet, 2019), ser en at elevene skal utvikle en helhetlig matematisk kompetanse. Bruker en Kilpatrick og kollegaer (2001) som kilde, kjennetegnes slik matematisk kompetanse ved fem komponenter:

• begrepsforståelse
• beregning
• anvendelse
• resonnering
• en positiv innstilling til faget

Komponentene stiller høye krav til undervisningen og utfordrer lærere til å engasjere seg i elevens tenkning. Det innebærer å stille spørsmål, observere og vurdere elevenes resonnement, språk og argumentasjon og bygge på dette i undervisningen gjennom å analysere og respondere på elevenes matematiske tenkning.

Ambisiøs matematikkundervisning bygger på noen viktige prinsipper, som at elever er opptatt av å skape mening og bør få like muligheter til å lære viktige matematiske ideer og tenkemåter. Slik undervisning forutsetter videre at lærerne behersker noen sentrale kjernepraksiser. Eksempler på kjernepraksiser er følgende:

• å lede undervisningen frem mot læringsmålet
• å få frem og respondere på elevenes resonnering
• å orientere elevene mot hverandres ideer og mot læringsmålet
• å sette høye krav til elevenes deltakelse
• å vurdere elevenes forståelse
• å bruke matematiske representasjoner

Det er disse praksisene for ambisiøs undervisning en tenker at det skal øves på i etterutdanningen. I MAM-prosjektet skjer dette gjennom at man øver på ulike praksiser gjennom læringssykluser.

Læringssyklus

Tretti matematikklærere fra mellomtrinnet ble i MAM-prosjektet invitert til å delta i sykluser med utprøving og utforsking (læringssykluser, figur 1) i en periode på to år. De hadde tolv samlingsdager, og ni var fulle læringssykluser (Fauskanger & Bjuland, 2019).

Hver syklus består av seks trinn:

1. Lærerne forbereder seg ved å se en film som viser gjennomføringen av en bestemt undervisningsaktivitet, og de leser utvalgte artikler.
   
   
2. Lærerutdanneren leder en felles diskusjon/analyse av filmen lærerne har sett, og artikkelen de har lest.
   
   
3. Grupper av lærere planlegger i fellesskap en bestemt undervisningsaktivitet for en elevgruppe. Lærerutdanneren veileder.
   
   
4. En av lærerne gjennomfører en øving av planen for undervisningsaktiviteten med lærerutdanneren og de andre lærerne i gruppen. Lærerutdanneren og de andre lærerne opptrer som elever. Underveis i øvingen kan alle deltakerne be om timeout for å stille spørsmål eller for å komme med alternative forslag til hva læreren kan si eller gjøre.
   
   
5. Den samme læreren prøver ut undervisningsaktiviteten med en gruppe elever. Underveis i utprøvingen kan læreren, lærerutdanneren eller de andre lærerne be om timeout for å stille spørsmål eller komme med forslag til hva læreren kan si eller gjøre.
   
   
6. Lærergruppen analyserer utprøvingen med lærerutdanneren som veileder. Deretter samles alle til en felles analyse av utprøvingen og forberedelse til neste undervisningsaktivitet

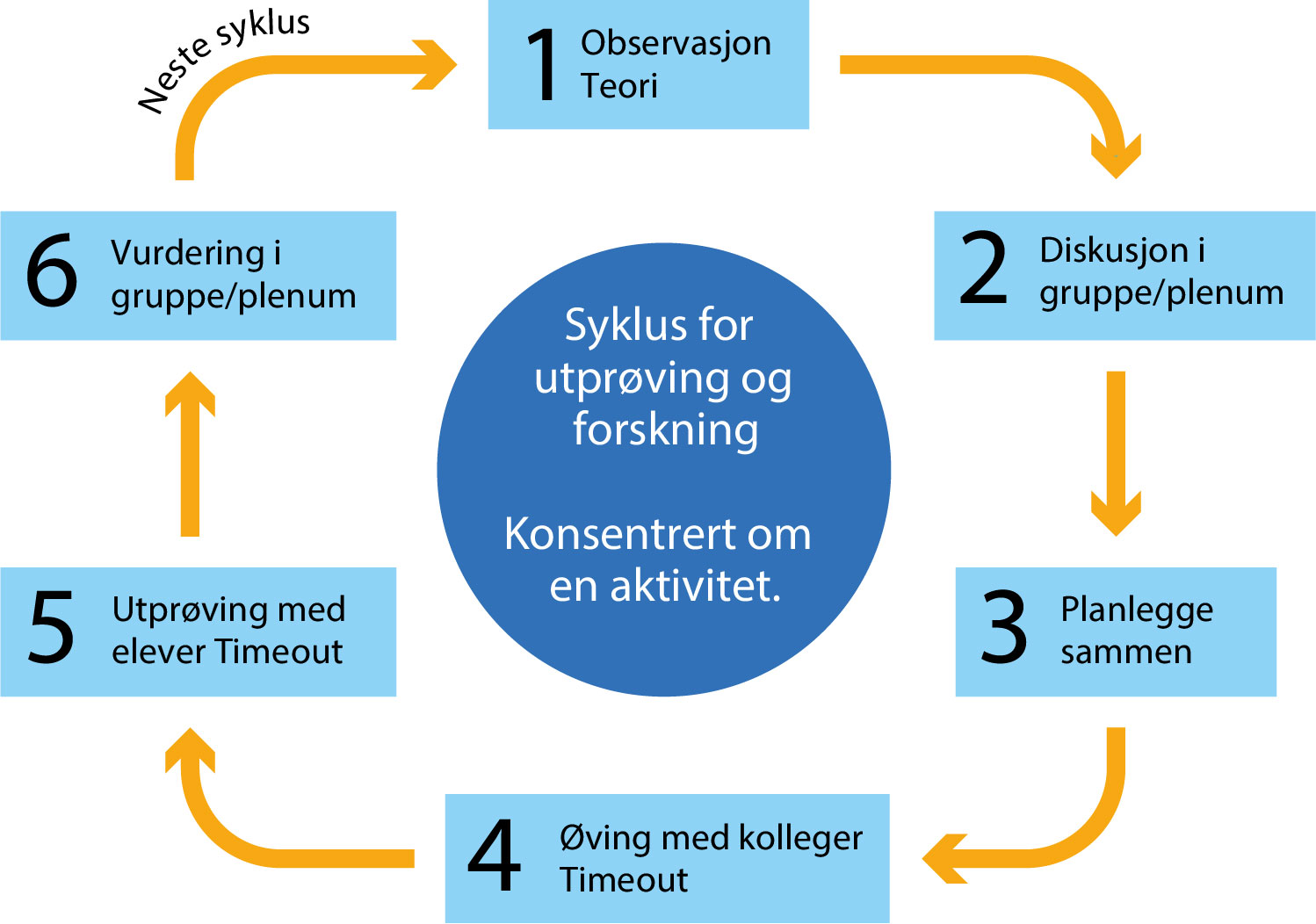
Gjennom deltakelse i sykluser som dette får lærerne anledning til å utføre og analysere sentrale praksiser i ambisiøs matematikkundervisning. I denne teksten vil vi se på øvingen, spesielt på dem som benytter seg av timeout som del av metoden.

Å øve på ambisiøse undervisningspraksiser

For at lærere skal lære ambisiøs undervisning, må etterutdanning baseres på noen spesielle prinsipper som kan sikre at utprøvingen skjer på en god måte (Kavanagh, Metz, Hauser, Fogo, Taylor, & Carlson, 2019). Et eksempel kan være en øving (punkt 4 ovenfor) der en lærer leder en gitt undervisningsaktivitet, mens alle de andre deltakerne opptrer som elever. Undervisningen kan stoppes når som helst gjennom at deltakerne ber om en timeout (f.eks. Fauskanger, 2019; Gibbons, Kazemi, Hintz, & Hartmann, 2017). Slik får deltakerne en mulighet til å arbeide sammen om å prøve ut og diskutere undervisningspraksiser mens de øver på undervisning.

Kavanagh et al. (2019) skriver at ved å redusere kompleksiteten i det å lære ambisiøse undervisningspraksiser gjennom å redusere valgene lærerne har i øvingene, så er det mulig «å fokusere på hvordan en best kan gi full oppmerksomhet til, forstå, og respondere på elevers ideer» (s. 11, min oversettelse). Wæge og Fauskanger (i trykk) fant at timeoutene i øvingene i MAM var settinger hvor deltakerne fikk mulighet til å diskutere mange ambisiøse undervisningspraksiser.

Et eksempel på bruk av timeout

Det følgende er et eksempel fra en timeout i en øving i MAM-prosjekt.

Timeouten er den fjerde i en 19 minutter lang øving. Timeouten varer i 3 minutter og 23 sekunder og har 74 utsagn. Aktiviteten i denne læringssyklusen er et kvikkbilde (figur 2).

I den felles planleggingen ble det bestemt at læringsmålet for elevene skulle være den distributive lov for multiplikasjon (a ∙ (b + c) = a ∙ b + a ∙ c). I begynnelsen av øvingen vises «elevene» et kvikkbilde i noen få sekunder. Læreren som leder øvingen (L), spør de andre deltakerne om hvor mange prikker de har sett, samt ber dem om å forklare hvordan de kom frem til antallet. Rett før denne time-outen har L skrevet to elevstrategier på tavla (figur 2). Det er lærerutdanneren (LU) som tar en timeout:

1. LU: Jeg tar en bitte liten timeout, jeg, for nå ser jeg at nå blir det litt trangt for oss (på tavla), ser dere det?
2. L: Ja.
3. LU: Sånn at det.
4. L: Skulle vi hatt dem større?
5. LU: Kanskje, eller at vi ikke skulle hatt dem på siden?
6. L: Disse her (peker på kolonnen med kvikkbilder til høyre)?
7. LU: Ja, disse skulle vært borte, jeg vet ikke.
8. L: For at vi kunne få plass til noe mer bortover her.
9. LU: Ja (går opp til tavla).
10. L: Ja, det var bedre plass i sted.
11. LU: Ja, for at vi hadde begynt å lage denne rekken (kolonnen) på siden (viser på tavla).
12. L: Jeg skal regne den her, ja.
13. LU: Jeg tror vi sletter dem her i første omgang også (sletter kvikkbilder fra høyre kolonne), sånn. For da får du til å skrive bortover, jeg tror det er...
14. L: Mm.
15. LU: Mm.

LU tok her en timeout for å rette deltakernes oppmerksomhet mot tavla. Hun mener det er trangt om plassen (1). L spør om de bør gjøre kvikkbildene større (4), og LU foreslår at de kan slette kvikkbildene i den høyre kolonnen, slik at de kan skrive elevens strategi ved siden av kvikkbildet (5, 7 og 13). L er enig (8, 10 og 14) og LU går opp til tavla og sletter de to øverste kvikkbildene i den høyre kolonnen (11 og 13). Som dette utdraget viser, åpner deltakelse i denne timeouten for en læringssituasjon for deltakerne, hvor de vurderer hvordan de best kan organisere tavla for å kunne representere elevenes strategier på en bestemt måte.

Bruk av samtaletrekk for målretta samtaler (Kazemi & Hintz, 2014), som oppmuntrer elever til å engasjere seg i matematiske samtaler, er en viktig del av MAM-prosjektet. Det er synlig i fortsettelsen av denne timeouten:

16. L: Ja, er det lurt å ta enda flere (elevstrategier) til å begynne nå, sant?
17. LU: Ja.
18. OL2 (OL= lærer som er elev): Men jeg tenkte på at kanskje, før de kommer med tankene sine, kunne det vært en idé å snakke sammen og forteller om «hva du så», eller er ikke det noe poeng?
19. L: Snu og snakk til å begynne med?
20. LU: Ja, hva tenker dere om det?
21. L: Før vi starter opp, ja.
22. OL2: Ja.
23. OL3: Da forlenger vi prosessen, tenker jeg.
24. OL2: Ja, men da føler jo alle at de har fått sagt sin del.
25. OL3: Ja, kanskje begge deler, men dette blir en ganske lang sekvens for å komme dit vi skal.

I linje 19–22 oppklarer deltakerne OL2 sitt forslag i linje 18, som er å bruke samtaletrekket «snu og snakk» før elevene presenterer sine strategier i plenum. Etter denne oppklaringen, og gjennom å indikere at samtaletrekket vil ta (for lang) tid (23 og 25), nøler OL3. OL2 støtter opp under sitt eget forslag i linje 16 ved å fremheve at «snu og snakk» gir alle elever mulighet til å presentere sine strategier (24). Fordeler og ulemper med samtaletrekket er en del av denne timeout-diskusjonen, som dermed er en mulig læringssituasjon for deltakerne – en situasjon hvor de får mulighet til å vurdere om og hvorfor samtaletrekk bør benyttes når de skal få frem elevers tenkning. Timeouten fortsetter med at deltakerne diskuterer hvor mye tid de har til å gjennomføre undervisningsøkten med elevene, og de enes om at de kan legge inn et «snu og snakk» (26–34). Basert på denne avtalen fortsetter timeouten slik:

35. L: De kunne ha snakket litt før de begynner å fortelle meg?
36. OL2: Det som er faren da, er at de kanskje kopierer det noen andre har sagt, da.
37. Flere: Ja.
38. OL2: Og ikke kommer med sin (strategi), fordi de kanskje ser at den andre sin er mer kjapp og finere.
39. Flere: Ja.
40. OL2: Og da får du kanskje ikke med den der 5 + 5 + 5.
41. L: Kanskje du får mindre variasjon.
42. OL2: Ja.
43. Flere: Ja.
44. OL3: Kanskje heller...
45. OL2: Du kan heller...
46. OL3: Kanskje heller snu og snakk når du har fått opp noen eksempler og spør «ser dere noen sammenhenger?»

I den felles planleggingen antok deltakerne at noen elever ville komme med strategien 5 + 5 + 5 + 4 + 4 + 4, og de bestemte seg for at de ville bruke den til å lede elevene mot målet for økten: den distributive egenskapen ved multiplikasjon (3 ∙ 5 + 3 ∙ 4 = 3 ∙ (5 + 4) = 3 ∙ 9). I denne delen av timeouten foreslår OL2 at noen av strategiene de diskuterte i planleggingen, kanskje ikke ville bli presentert i plenum om elevene snakket sammen før de presenterte sin egen strategi (36, 38 og 40). De risikerer at 5 + 5 + 5 ikke vil bli foreslått (40) av elevene etter at de har snakket med medelever, som kanskje har strategier de opplever som «kjappere og finere» (38). Basert på diskusjonen enes de om at det å invitere elevene til å snakke sammen kan redusere antall strategier (41–43). Fordeler og ulemper ved å bruke samtaletrekk er også en del av denne timeout-diskusjonen, men mens den første delen av diskusjonen var knyttet til tidsbruk (23–34), er det nå faren for at «snu og snakk» gir mindre variasjon i elevstrategier. Med dette som bakteppe foreslår OL3 at de heller kan bruke «snu og snakk» «når du har fått opp noen eksempler og spør ‘ser dere noen sammenhenger?’» (46). Som dette utdraget illustrerer, åpner deltakelse i denne timeout-diskusjonen opp for en læringssituasjon der deltakerne kan vurdere hvorfor og når det er fornuftig å bruke samtaletrekket «snu og snakk» når de skal få frem elevers strategier. De diskuterer også hvorvidt dette samtaletrekket er en støtte for å nå målet. Deltakerne skaper sammen forståelse for praksiser som å få frem elevers tenkning, bruk av samtaletrekk og det å arbeide mot et gitt mål for en undervisningsøkt. Målet de har satt for økten, er implisitt synlig i diskusjonen, men blir eksplisitt diskutert i fortsettelsen av timeouten:

47. L: For vi sa vel at vi skulle bruke den (snu og snakk) etter at, eller når vi skulle begynne å få dem inn på målet vårt.
48. Flere: Ja.
49. L: Men det kan vi jo bli enige om.
50. Flere: Ja.

I dette utdraget minner L de andre deltakerne om at de i planleggingen ble enige om å invitere elevene til å snu seg og snakke sammen når de skulle arbeide for å nå målet for timen (47), og de andre deltakerne husker hva de ble enige om (48 og 50). Deltakerne er engasjert i en diskusjon av praksisen med å legge til rette for at elevene får snakke, samtidig som de arbeider for å nå målet for timen. Siste del av denne timeouten fortsetter slik:

60. OT2: I forhold til denne her å skrive de sånn under hverandre, er det kanskje bedre å skrive det bortover? Og pluss …
61. OT4: Og skrive opp stykket.
62. OT2: Da kommer vi fortere til den.
63. I: At jeg skriver...
64. OT4: Tre ganger fem pluss tre ganger fire.
65. I: Mm, med en gang.
66. OT2: Ja.
67. I: (skriver 3 ∙ 5 + 3 ∙ 4 på tavla) Ja, for nå fikk vi plass til det.
68. Flere: Ja.
69. TE: Og det tenker jeg kanskje at det er litt viktig på den fire pluss fire pluss fire, og at den og blir skrevet.
70. I: (starter å skrive) Skal jeg kjøre på med parentesene og?
71. TE: Jeg tenker at det trenger du ikke der.
72. I: Nei (skriver 4 + 4 + 4 etter 5 + 5 + 5, som allerede står på tavla).
73. Flere: Mm.
74. I: Yes.

Denne delen av timeouten starter med en diskusjon av hvor og hvordan skrive elevstrategier på tavla (60–61). Dette fremheves som viktig knyttet til å arbeide mot målet for timen (62). Flere deltakere (64, 66 og 68) støtter L (63, 65 og 67) i avgjørelsen av hvor og hvordan elevstrategier skal skrives på tavla. Hvorvidt de skal bruke parenteser når de skriver elevstrategiene på tavla, inngår også i diskusjonen (71-75). Forslag om hvilke elevstrategier en vil trekke frem for å nå målet for timen, diskuteres også (64 og 69), og L skriver de foreslåtte strategiene på tavla (70). Deltakerne i denne øvingen får dermed mulighet til å lære hvor, når og hvordan de skal skrive elevstrategier på tavla for på best mulig måte å jobbe mot målet for timen.

Øvingen fortsetter etter denne siste delen av timeouten. Læreren som leder øvingen, spør de andre deltakerne (som elever) om de har andre strategier for å finne antall prikker i kvikkbildet.

Et godt tilbud, selv for erfarne lærere

Målet med ambisiøse praksiser i matematikkundervisningen er at alle elever skal utvikle dybdeforståelse (Lampert et al., 2013), og det å lære slike praksiser er en kompleks og utfordrende prosess. Etter å ha analysert 175 timeouter i 18 øvinger har vi funnet at deltakerne gjennom å stille spørsmål, gi hverandre tilbakemeldinger og diskutere konkrete forslag til hva læreren med ansvar for øvingen kan gjøre i en gitt situasjon, bygger på viktige prinsipper for ambisiøs undervisning. Deltakelse i timeout-diskusjoner i øvinger åpnet opp for læringssituasjoner for deltakerne, hvor de sammen kunne utfordre og utvikle flere ambisiøse praksiser samtidig. De får dermed muligheten til å lære om sammenhenger mellom de ulike praksisene. Eksempler er organisering av tavla, når de skulle representere elevers strategier på tavla, og når de ville at elevene skulle få mulighet til å se sammenhenger mellom de ulike representasjonene (linje 1–15). Deltakerne diskuterte også hvordan en praksis kunne påvirke en annen. Eksempelvis diskuterte de hvorvidt og når de skulle bruke samtaletrekket «snu og snakk» for å støtte samtaler mellom elever når målet var å få frem elevenes strategier samtidig som de arbeidet mot målet for timen (linje 16–59). Videre ble betraktninger knyttet til én praksis diskutert i tilknytning til en annen praksis. Deltakerne arbeider mot målet for timen samtidig som de også vurderer hvilke elevstrategier de skal konsentrere seg om for å nå målet for timen. Dette er synlig i linje 60–74, hvor deltakerne diskuterer hvor, når og hvordan de skal notere hvilke elevstrategier på tavla. Gjennom å redusere deltakernes valg i øvinger, gir timeouter deltakerne mulighet til å prøve ut og diskutere, og dermed lære, flere praksiser som verdsetter elevers respons i relasjon til hverandre (Kavanagh et al., 2019; Lampert et al., 2013; Lave, 1991).

Jeg håper at jeg med dette har fått fram hvor nyttig det kan være å øve på matematikkundervisning som en del av etterutdanning – selv for erfarne lærere.