Introduction

Programming is currently making its entrance into the mathematics classroom in Nordic countries (Bocconi et al., 2018). With the coupling of mathematics and programming comes a range of possibilities and challenges for learning. Possibilities can take the form of numerical methods and simulations in addition to new ways to teach, learn, and investigate mathematics. Adversity, the focus of this article, can take the form of increased difficulty and complexity, leading to frustration and loss of motivation. In this work, adversity is a combination of two terms used in the theory: obstacles, from the theory of didactical situations (TDS) in mathematics (Brousseau, 1997) and barriers, from the programming community (Ko et al., 2004). When referring to an obstacle, it is mathematical; when referring to a barrier, it is related to programming.

Barriers from the programming community are a combination of syntax errors, structural errors, logical challenges, error handling, and the number of commands available (Ko et al., 2004). Obstacles from the mathematics community are extensive and span a wide selection of areas, from learning the number line in primary school to learning to differentiate and integrate in upper secondary school (Campbell & Epp, 2005; Merenluoto & Lehtinen, 2004; Nelson & Powell, 2018). Obstacles are important in the process of learning (Lodge et al., 2018), and knowing which obstacles lead to confusion and frustration can facilitate learning (D’Mello et al., 2014). Obstacles leading to confusion are closely connected to learning in that confusion can have beneficial effects, most importantly when it is resolved (D’Mello & Graesser, 2014). A challenge for educational researchers is to determine which adversities exist and which may lead to learning processes and outcomes (Lodge et al., 2018). As Niss (1999) stated, if we know the obstacles that block the paths of students learning mathematics, we will gain a better understanding of how mathematical knowledge and ability are generated and activated, leading to better learning.

Research has addressed the barriers encountered when learning programming (e.g., Grover & Pea, 2013; Jenkins, 2002; Ko et al., 2004; Piteira & Costa, 2013) and the kinds of adversities students encounter when learning programming as part of mathematics (Benton et al., 2017; Benton et al., 2018). The barriers within programming and the obstacles within mathematics are significant, and this article uses an abductive framework to categorise the adversities met by secondary school students utilising programming in mathematics. In this study, mathematical obstacles experienced by students were continuously investigated and, to explore the mathematical programming adversities they encountered, a framework from word problems (Verschaffel et al., 2020a) was used. An adversity is defined as a situation in which the students display uncertainty regarding how to proceed with the mathematical programming problem (MPP) on which they are working.

This article investigates the kinds of adversities students encounter when using programming as a tool in mathematics. As well as suggesting how to avoid adversities which do not facilitate learning, this work will aid in both teachers’ orchestration of mathematics classes using programming and in the design of MPPs. The two research questions are:

What kinds of adversities do upper secondary school students encounter when working with MPPs in the mathematics classroom?

How are the adversities related to the learning of mathematics?

The aim is to increase our knowledge of the kinds of adversities that block the paths of students learning mathematics, thus facilitating learning. Following the investigation, suggestions are made on how to mitigate undesirable adversities through both task design and classroom orchestration to facilitate learning.

Mathematical programming problems (MPPs)

MPPs consist of a series of tasks in which students work on building a program to solve a mathematical problem. To facilitate adidactical situations (Brousseau, 1997), where the students work autonomously and learn by adapting to the milieu, I have structured the MPP using the seven steps presented in Figure 1.

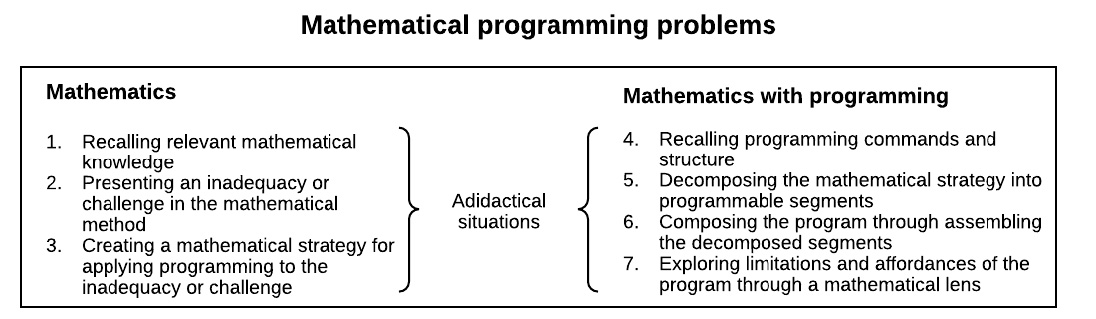
The structure of the design is the product of a three-year iterative process implementing MPPs among Norwegian upper secondary school students of mathematics. The iterative process consisted of moving from a simple ‘build a program that …’ to decomposing the MPP into several smaller tasks, with questions and activities facilitating discussion and exploration by the students. As a brief example, I use the building of a program calculating the zero point of a function using the bisectional method. Step 1 consists of asking the students to find the zero point of several different kinds of functions, illustrating the different methods required for each kind. Step 2 asks them to find the zero point if the function does not conform to any known method, such as 𝑓𝑓(𝑥𝑥) = ln(𝑥𝑥 + 2) − 𝑥𝑥. In step 3, one student takes the role of a ‘program’ and is given a set of graphs where the function is unknown but the zero points are given. The other members of the group are tasked with finding the zero points by giving the ‘program’ x-coordinates, and the ‘program’ can only respond with the corresponding function value. This allows exploration of several strategies for finding the zero point to be evaluated and tested. Step 4 allocates tasks requiring students to recollect necessary programming structures and commands, such as plot commands and while loops. Step 5 consists of transforming the method discovered in step 3 into a coding structure, and step 6 consists of building the program. Both steps 5 and 6 contain tasks to assist in aspects of the building of code, such as the conditions for the while loop. The final step asks the students to evaluate the program, investigate whether it works for all functions, and, if there are functions for which it does not work, determine why. Themes for the MPPs included in this study are

(1) the quadratic equation, (2) using the bisectional method of of finding the zero point, (3) differentiating a function numerically*, and (4) using Newton’s method of finding the zero points**.

*differentiating a function numerically:

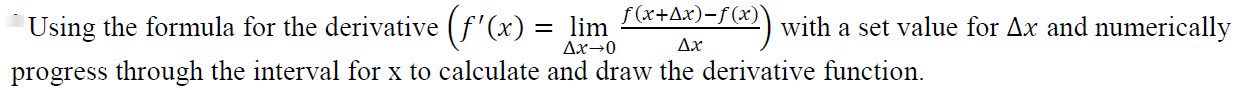
using Newton’s method of finding the zero points**:

Theory

To discuss the adversities students encounter when working on MPPs, adidactical situations from TDS were applied. An adidactical situation occurs when the students interact with the milieu, consisting of their peers, the tools, and the design of the problems, and take the initiative and have the responsibility for the outcome. In TDS, the obstacles the students encounter are separated into three kinds (epistemological, didactical, and ontogenic) (Brousseau, 1997), which are used in the discussion of this article. Epistemological obstacles are beneficial and sought after since they force the students to reorganise their knowledge to fit a new situation. Typically, the students are presented with a problem for which their previous knowledge is insufficient or wrong, and this forces them to apply their existing knowledge in a new way. An epistemological obstacle is the desired type of obstacle, facilitating learning as the students overcome the obstacle. Ontogenic obstacles originate from the lack of the knowledge required to make the connection necessary to solve the designed task. Didactical obstacles are caused by erroneous or flawed task design which leaves the students unable to complete the task. Whereas ontogenic obstacles lie more with the students and teacher, didactical obstacles belong firmly to the designer of the task. Obstacles can facilitate learning, such as epistemological obstacles, or hinder or limit it, such as ontogenic and didactical obstacles (Brousseau, 1997). The observed obstacles therefore influence the design, since both ontogenic and didactical obstacles can be mitigated through a design process.

Word problems

The transformation of a mathematical model into a programming code is similar to the internal construction of a model within word problems, after which it is implemented into a mathematical model. The building and running of a program are like working through a mathematical model to derive a mathematical result. Interpreting and evaluating whether the outcome or output is correct and reasonable is equally important. Finally, communicating the result of the calculation or providing a descriptive output from the program occurs in both instances. Given all these similarities, the implementation of word problem strategies (Verschaffel et al., 2020a; Verschaffel et al., 2000) and adversities was an important starting point for building the framework and performing the analysis of the obstacles encountered by students when solving MPPs.

A word problem is defined as a verbal description of a problem situation where one or a series of questions is posed whose answer can be reached through the use of mathematical operations and numerical data contained within the problem statement (Verschaffel et al., 2000). As with all kinds of problems, what constitutes a problem for one student may not be a problem for another (Muir et al., 2008). Whether a task constitutes a problem depends on several factors, such as familiarity with the type of problem, ability to recall required knowledge, and the tools available (Verschaffel et al., 2020a; Verschaffel et al., 2020b). The pathway through a word problem is complex, but central aspects of the process are contained within the six phases outlined below (Verschaffel et al., 2020a), which have similarities to the structure (but were not used in the design) of the MPPs (Figure 1).

1. Internal construction of a model depicting the problem, understanding each element and their relation.
2. Transformation of the model into a mathematical model in which the elements and their relation are essential for the solution.
3. Working through the mathematical model to derive a mathematical result.
4. Interpreting the outcome of the computational work.
5. Evaluating whether the outcome is computationally correct and reasonable.
6. Communicating the result.

This is not a sequential model, as there is room to move back and forth and skip phases, depending on student knowledge. Research into word problems indicates that the main obstacles encountered by students are text comprehension, numerical complexity, and the connection between the two (Daroczy et al., 2015; Pongsakdi et al., 2020). These obstacles share properties with both ontogenic and epistemological obstacles (Brousseau, 1997). Given both the known obstacles and the model above, suggestions have been made of how to build a word problem encompassing three main characteristics (Verschaffel et al., 2020a). Firstly, the use of varied, cognitively challenging, and/or realistic tasks lowers the chance that students develop superficial strategies and encourages them to discuss different kinds of models to apply, facilitating adidactical situations (Brousseau, 1997). Secondly, providing the students with both scaffolding to solve the problem and the ability to experiment with and discuss the problem hinders ontogenic obstacles and builds towards adidactical situations. Thirdly, creating a classroom conducive to the discussion of mathematical problem solving, for instance problem-solving strategies such as those proposed by Polya (1957), further facilitates adidactical situations. Word problems aim to motivate students to study mathematics, facilitate creative thinking, develop their problem-solving abilities, and assist in the development of new mathematical concepts and skills (Verschaffel et al., 2000).

Programming barriers

Challenges in learning programming have been investigated frequently (Medeiros et al., 2018; Piteira & Costa, 2013), and this article focuses on the learning of programming syntax and sequences of variables, loops, and conditions, as these are both the most applicable to a school setting and present a significant challenge to learners (Bosse & Gerosa, 2016). Ko et al. (2004) refer to six barriers in the programming process, three of which are closely related to programming in a school setting. The first is selection barriers, which relate to the programming interface and the knowledge of what tools and commands to use to build for a result. The second is understanding barriers, which consist of knowledge of how to handle errors and unexpected behaviour of the program. Error handling is a recognised challenge within programming education (Lahtinen et al., 2005). The third is information barriers, in which the program did not confirm the result or behave in accordance with the hypotheses, which often results in the inability to evaluate what went wrong. All three of these barriers are related to the evaluation, rather than the execution, of the program. The students’ evaluation and discussion of a mathematical problem is central to the adidactical situation. Ko et al. (2004) further divided the barriers into subgroups of surmountable and insurmountable barriers. Surmountable barriers are those the students are able to overcome; when the complexity or number of barriers becomes too large, the students are unable to continue and face an insurmountable barrier. Surmountable barriers bear a resemblance to epistemological obstacles, and insurmountable barriers bear a resemblance to ontological obstacles (Brousseau, 1997).

Most school students are novice programmers, who are limited to surface knowledge of programs, typically using the ‘line by line’ approach instead of meaningful program building (Lahtinen et al., 2005). Students often have knowledge of both the syntax and the semantics of programming but lack the ability to combine them into valid and efficient programs (Winslow, 1996). Despite several attempts at designing strategies to support novice programming (such as collaborative teamwork, peer tutors, workshops, and forums), multiple adversities remain when students are introduced to algorithmic thinking (Stephens & Kadijevich, 2020), logic, and problem solving. The difficulty of algorithmic thinking combined with the exhausting labour of learning syntax generally leads to frustration, rejection, and poor vision (Buitrago Flórez et al., 2017).

Method

Implementation and data collection

MPPs were implemented in a classroom over a period of two years (2018–2020) in an advanced mathematics course for students (N=28) in the last two years of secondary school (age 17–19). The students received some basic knowledge of programming from a 10-hour crash course in Python programming which included variables, input and print, mathematical operators, conditional statements, and loops. The students participated in a total of 10 lessons during each school year in which programming was used. For each lesson (90 minutes), the same two groups of two and one group of four students were recorded while working on the task. The grade average of the class was 4.3 (on a scale from 1 to 6, where 6 is the top score), and the class consisted of students spanning the entire grade spectrum.

The students were informed of the implementation prior to their subject election so they could elect not to be a part of this specific class. Initially, there was a concern that this would reduce the validity of the research due to a reduced number of participants and that only either high-achieving students or those with prior knowledge of programming would participate. A review of the students’ mathematics grades from the previous year and an anonymous survey asking the students for their knowledge of programming revealed that neither concern was borne out. The three groups consisted of four males, two females, and one male and one female, respectively, all of whom collaborated well throughout the year. The students were told to discuss any adversity within the group before requesting help from the teacher. The data collection consisted of a recording of each student’s computer screen together with their voice. Each student in each group had a screencast program installed on their school laptops and was given a lavalier microphone to ensure the best recording of their voice.

Data analysis and analytical framework

The screen and voice recordings for each member of the group were digitally combined to form one video file with two to four screens and an audio where all the students’ voice recordings were added together. This facilitated transcription, as viewing all the screens together allowed transcribers to clearly see where each student was in the process of building the program, and the combination of voice recordings made the voice of each student very clear, allowing for an accurate transcription. Every part of the group discussion relating to mathematics was transcribed. Non-mathematical discussion was noted, as it may be important to learning (Ryve, 2011; Wegerif, 2007), but not transcribed. On average, each group had one to two minutes of non-mathematical discussion every 20 minutes. The next step was dividing the transcript into segments where the students encountered an adversity when working on the MPPs. Afterwards, a second reading was performed to categorise what kinds of adversities were present in each segment and whether they were resolved. This process was an abductive one whereby each segment was read, and the kinds of adversities were described in detail and then compared with the programming barriers from Ko et al. (2004) and obstacles from TDS (Brousseau, 1997). After an initial framework was created, the transcript was re-read to investigate similarities between segments and their accompanying categories with the aim of uncovering broader categories. As an example, it quickly became apparent that several adversities consisted of the students forgetting either the name or the properties of a command or type, leading to a category called concept adversities. A similar process led to the uncovering of the remaining three categories. After the categories were decided, another reading of the segments was performed to ensure that the categories covered all the adversities in the transcript and that each segment could be coded by the framework I designed, consisting of concept, syntax, output, and coding.

Concept adversity is related to the use and knowledge of different commands, methods, and types in a programming language and encompasses everything from not recalling a command to not understanding what a command does or a type represents. It corresponds to the selection barriers of Ko et al. (2004) and the ontogenic obstacles of Brousseau (1997). Syntax is closely related to concepts but is a separate category, being more closely related to the logical aspect of programming. Syntax includes the structure of conditions and loops and the logical build of a program. A program calculating the square root of a number first needs to check if the number is positive or zero before calculating; otherwise, there will be an error. Errors in syntax are related to the student’s internal construction of a model depicting the problem, understanding each element and the relation between them (Verschaffel et al., 2020a).

Output is when the result after pressing the ‘run the program’ button presents an adversity, which can take many forms, from syntax errors and unexpected answers to no output at all. Some forms are simple, such as errors concerning a missing bracket indicating an understanding barrier, and some are complex, such as unexpected or no outputs that are hard to evaluate, indicating an information barrier (Ko et al., 2004). Interpreting and evaluating the outcome of the computational work and whether it is correct and reasonable (Verschaffel et al., 2020a) is expected, and the more difficult an output is to evaluate, the more it hinders an adidactical situation. Coding is when the students are converting a mathematical procedure to programming code, which is the transformation of the model into a mathematical model (Verschaffel et al., 2020a). The process of transposing a mathematical idea or method to a working programming structure is of particular interest as it facilitates students exploring mathematical methods and concepts with the logical structure of programming to develop an in-depth understanding of mathematics. The exploration also facilitates adidactical situations.

Each adversity in our study had an additional code, which distinguished whether the adversity was resolved or not. The framework is presented in Table 1, which shows the subcategories and gives examples from the transcripts.

The framework allows the investigation of four kinds of adversities that affect the interaction between students and their progress through the task. Adversities that are resolved are of special interest since they are closely related to learning (D’Mello et al., 2014), and the framework allows us to distinguish both the type of adversity and how often adversities are resolved. The transcripts presented in the results include extracts from each of the four categories. All the adversities were coded into one or more of the categories. Each excerpt is presented to illustrate a type of adversity and followed by an explanatory description. When a diversity within a category was observed, two or more excerpts are presented to illustrate the similarities and differences between the kinds of adversities.

Table 1. Framework for investigating the adversities encountered by students when working on MPPs

Results

The design of the MPP facilitated the students’ discussion throughout the lesson, allowing for an extensive investigation. The excerpts illustrate the differences between the kinds of adversities observed. Throughout the lessons, segments with adversity occurred 41 times in the transcripts. An adversity segment spanned everything from a brief discussion of only a couple of interactions to discussions lasting several minutes within the group. In 11 of the adversity segments, there were occurrences of multiple categories, which explains the sum of occurrences equalling 60.

Table 2. Numerical results of analysis of transcript

In the transcripts, < > is used to indicate an action or emotion not explicitly referenced, and [ ] is used to explain references and implied words used by the students. Students’ references to programming code or feedback from the program are marked with * *. Each excerpt is coded with a letter to indicate the category, as per Table 2. A few of the transcripts are shown with the accompanying code being discussed by the students to illustrate the origin of the discussion. However, most of the code sequences being discussed by the students are too long to be displayed properly.

Concept adversities were present in 18 of the segments. Within this category, recollection of the properties of a command or type occurred 11 times, making it the most prominent occurrence, with the return command used in a function being the most prominent. The first excerpt reveals the student does not recall the properties of a command, but the adversity is resolved with help from the group.

C-00 F: What does that *return* mean? C-01 M: I know that.
C-02 F: What does it mean?
C-03 M: When you [the program] calculated … it [the return command] gives back the y-value [the return value], if not then it would have calculated it and … only the PC would know it [as if it is not possible to use the result later in the program], but now it has calculated and gives back [to the program] what it [the y-value] is.

Student F was looking at an example applying the use of a function and trying to understand and replicate the structure but did not fully understand the return command (C-00). Student M contributes with an understanding of the command (C-03). Conversations concerning the return command occurred in several lessons and, unlike in the above transcript, did not always lead to a resolution. Students unable to recall a specific concept slightly reframe their question. When they recall a command, but not its properties, such as with the return command, they often ask, “What does <command> mean/do?”, but when they do not recall the command itself, they formulate questions in the form of “How do/can I <perform the actions of a command>?”, as presented in the excerpt below.

C-10 M: How can I program so that it [the program] asks the user to type in the expression?

The student, M, is trying to build a code where the program asks the user to input a polynomial function and is unable to recall the input command (C-10). All instances of concept adversity were of this type, and they were usually solved (14 out of 18). When concept adversity was not resolved, the students continued using the command or type without indicating that they had knowledge of its purpose (C-21).

C-20 F: What is *float*?
C-21 L: I do not remember, but it was written on the other [program from previous lesson].

Syntax adversities were present in 10 segments; defining variables occurred 6 times, making it the most prominent. The first adversity is the program returning an error where a name [variable] is not defined, as shown in the excerpt below.

S-00 M: *Error name y is not defined*, but y is, darn it, defined here [refers to program].
S-01 L: No, but that is not … yes, but you need to define y under here [points to another part of code], *y equals function value*.

Student M runs the program and receives an error that y is not defined and displays frustration, being sure that y is, in fact, defined (S-00). L then corrects the statement, pointing out that while M has defined y, the placement of the definition is wrong within the code (S-01). Each adversity regarding variables is similar: the students think they have defined a variable, but they are either using a wrong variable name or misplacing the definition within the code, indicating a misunderstanding of the sequential reading of the code, and displaying frustration (S-00).

Another syntax adversity is the placement of code segments, where the students are uncertain of where to put a new code segment. In the transcript below, the students, having plotted the graph of a function, are now adding a code asking for two x-values to calculate the zero point of the function using the bisectional method.

S-10 M: Where are we going to input this [segment of code]?
S-11 A: Yes, that’s what I am thinking about. Is it after *y equals the function of x*?
S-12 M: No, because you have written *axhline* [command for drawing a horizontal axis].
S-13 A: Is it over the definition of the function?
S-14 M: It is all the way at the bottom [of the programming code].
S-15 A: It is at the bottom.
S-16 M: Yes, I think so, because we have written *axvline* [command for drawing a vertical axis] and so on at the bottom.
S-17 A: That is just the axis. That has nothing to do with what we input. S-18 A: I think we type it after *y equals function value*.
S-19 H: Yeah, yeah, I agree.

The three students are discussing where to input a code segment (S-10, S-13, S-14, S-18) and their reasoning behind the placement (S-12, S-16, S-17). The last syntax adversity that occurred is the sequential reading of code relating to the structure and function of if statements and for and while loops. The excerpt below shows students building a program using a while loop to find a good numerical estimate for a zero point.

S-20 L: Because I have used the *while* loop, so now it keeps …
S-21 F: … keeps [running] until it finds the zero point.
S-22 L: Yes, and it looks like it is correct if you look here [refers to correlation between the output and the plot of the graph], but what is kind of stupid is that we have three zero points.
S-23 F: Oh.
S-24 L: Let’s try again and see if we can find the other zero points.
S-25 F: And how do you propose we do that?
S-26 L: I think that we take like one and then <runs program and types in 1 as a starting guess>.
S-27 L: Yeah! <surprised voice> 2.16 [the correct x-value for the zero point].
S-28 L: We have managed to find the zero points.
S-29 F: But we want to get all of them at the same time, but it is not possible … because now we have guessed the three zero points. Is there no way we can guess and then receive all the zero points?

The program runs as it should (S-22, S-27), but the cubic function the group investigates has three zero points, and the program is only able to find one zero point at a time (S-29). In the final statement of the excerpt (S-29), the student evaluates the program and initiates a group discussion of ways to receive all zero points at the same time (not displayed). Syntax adversities were solved 7 out of 10 times. When a syntax adversity was not resolved, the students either gave up or deleted the code segment and started over.

Output adversities consist of adversities occurring due to the feedback from the editor as the students execute their program. Students understanding (6 instances) or not understanding (7 instances) the error they receive represents 13 of the 18 occurrences of output adversities. When a student does not understand the error (as seen in O-00), they display frustration and openly say that they do not understand what has happened. In the excerpt below, the student continues to get an error when running the program.

O-00 L: Oh <swear word>.
O-01 L: It is just exciting to watch me fail again and again.
O-02 L: I do not understand what is wrong, but there is something wrong. It says *invalid syntax*.
O-03 M: Oh, then you have a parenthesis wrong.

Student L displays frustration and does not seem to know how to handle a syntax error (O-02). Student M then offers a possible solution to the problem (O-03), which, after a short discussion, resolves the error. On other occasions, students do understand the error, in which case they display less frustration and vocalise an idea for resolving the adversity (S-01). In the transcript below, the students are building a program to solve a quadratic equation and receive an error due to a negative value in the discriminator (O-10). One student quickly suggests the implementation of an if statement to investigate the sign of the discriminator prior to using the quadratic formula (O-11). This is evident from the following actions taken by the student, where the above if statement was coded (not shown in transcript, but in video recording of the screen).

O-10 M: Oi *x1 equals nan*, *x2 nan*.
O-11 M: So therefore, we should perhaps include an *if* [statement].

There is also the possibility of an unexpected answer, when the program outputs something that the students did not anticipate (O-10 and O-22), resulting in a discussion including evaluation and exploration. The excerpt below is taken from students solving a quadratic equation using the quadratic formula.

<Student A runs a program with values 𝑎𝑎 = 4, 𝑏𝑏 = 0, and 𝑐𝑐 = −49>.
O-20 A: Does that make any sense? That makes no sense.
O-21 H: What?
O-22 A: Why? 56? What do you mean by that? It should be 3.5 which is what it is, but this is … this is very strange.

Following this excerpt is a long discussion involving the entire group about what is wrong. They eventually resolve the unexpected answer and discover that they have forgotten to put the denominator in brackets (as in /2 ⋅ 𝑎𝑎 instead of /(2 ⋅ 𝑎𝑎)). The final output adversity observed is when no output is yielded after running the program. In the transcript below, the students are building a program utilising Newton’s method for finding the zero point of a function, have just implemented the formula, and are now running the code for the first time.

O-30 L: Ok, *input an x-value* [to initialise Newton’s method] ... and then we need to plot the tangent line.
O-31 F: Eight.
O-32 L: Ok, eight.
<types eight, runs program, no output>
O-33 L: Ok, I think this works, but now we need to plot the tangent line ... we have forgotten that.
O-34 F: But can we not write here [in the function calculating the next guess] ... like… *return*?
O-35 L: *Return* <types>.
O-36 F: *xn*?
O-37 L: *xn* <types> [the result from Newton’s method].
<types eight, runs program, no output>
O-38 F: If you write like seven [as a starting guess]?
<types seven, runs program, no output>
O-39 F: No.

Students L and F run their program but receive no output. They try to alter the program (O-33 – O-37) and alter the input value (O-38), but there is still no output (O-39). The program generates no error, and the students display uncertainty about where the error in the program resides. They end up deleting the code snippet and starting over. Output adversities were solved in 15 out of 18 instances.

When the students received no output, the adversity was sometimes not resolved, and the students then deleted code and wrote a new code segment.

Coding adversities consist of adversities converting a mathematical procedure into a programming segment, which occurred 14 times. Each segment differs, since each applies to a separate mathematical idea to be converted into programming code. In the first excerpt, the students have worked through an exercise using Newton’s method to find the zero point by drawing tangents for x-values close to the zero point. They have also been given the formula of Newton’s method and are now trying to implement the method into programming code.

D-00 F: We need to create a tangent line for the …
D-01 L: Yes, and then we can write … *plot* … no, ok.
D-02 F: or …
D-03 L: *def tangent of x* [Python code], like that and …
D-04 F: What are we going to write here [in the program function]?
D-05 L: … and that is x.
D-06 F: *x equals*.
D-07 L: *xn*, wait a little.
D-08 F: *xn*.
D-09 L: *Equals … xn minus one*? I feel this is going to fail. *Minus f of xn*.

The students are discussing how to proceed, including using the tangent (D-00) before applying Newton’s formula (D-03). At the end of the transcription segment, they foresee that their code is going to fail (D-09). The ideas displayed are well founded, but the implementation into the programming editor shows uncertainty. The second transcript is taken from when the students are building a code determining whether two variables have non-identical sign values.

D-10 H: What is a quick way to check if two numbers have the same or different signs with the help of an *if* statement? …
D-11 H: A quick way to check if two numbers have the same or different sign …
D-12 A: Perhaps setting the function value equal to *a* [a variable] or something, then *if a* [programming code], the function values, if *a minus b* is positive then something.
D-13 M: It becomes ‘if the sign is the same’, but …
D-14 M: There is no command [in Python] for sign, that would have been nice.
D-15 H: That would have been digg [Norwegian slang for nice].

Student H is stating the question to the group (D-10), and they are discussing how to make the program distinguish between the signs of two values (D-12). The task indicates the use of an if statement, but no other help is given, and they know of no command that performs this procedure. The short excerpt is the start of a longer discussion over several minutes in which several mathematical procedures are brought up and evaluated.

The last coding excerpt displays the challenge of expanding a working program to generalise it. The students have built a program solving the zero points of a quadratic equation using the quadratic formula and are now asked what happens when the value of the quadratic coefficient is zero.

D-20 M: Ok, test the program for several functions. Does it always work? It always works! What happens if you test for …
D-21 A: It always works?
D-22 M … for 𝑎𝑎 equal to zero [the 𝑎𝑎 in 𝑎𝑎𝑥𝑥2 + 𝑏𝑏𝑥𝑥 + 𝑐𝑐].
D-23 A: What did you do...?
D-24 M: That does not work! <Emphasis on ‘that’>
D-25 M: But then … we must, oh must we do that? Bro. Then we must change the *if* statement. Then we need two *elif*’s [else if statement in Python], is that allowed?

The students are reading the task (D-20, D-22) and then display realisation that the program does not work in the situation where 𝑎𝑎 equals zero (D-24). The proposed solution is the inclusion of another set of if statements, and they question whether this is possible within the code (D-25). Coding adversity was solved 13 out of 14 times. The only time a coding was not resolved was when a student confused the mathematical definition of a function with the computational use of a function.

Discussion

The analysis shows how different kinds of adversity manifest when students work on MPPs and the complexity of these adversities. Concept adversities are the least surprising type and are an instrumental process that rarely contributes to mathematical learning. Concept adversity was present in all lessons and spanned a range of different commands and types, all falling under the selection barriers defined by Ko et al. (2004). The change throughout the lessons was that the concept adversity varied as the students became more comfortable with certain programming commands and structures. Differentiation between types, typically whole numbers (int) and decimal numbers (float), was present in the initial lessons; in the later lessons, however, it disappeared in favour of more complex commands, such as the return command. When the students tried to recall a command that performed a certain property, they often vocalised why they needed the specific command (C-10). I would argue that the recalling of properties of a given command or type (C-00 and C-20) is less advantageous than asking how to perform a certain action (C-10). The latter results from the students’ exploration and evaluation of the program and what the next step in the logical order is. Concept adversities, whether resolved or not, accounted for a small part of the lessons’ overall duration and were not observed to interfere with the students’ mathematical progression through the task. Designing MPPs to incrementally increase the number of commands needed (Verschaffel et al., 2020a) was observed to work well. One could possibly reduce the concept adversity further by giving the students a command cheat-sheet as a handout. While concept adversity is primarily a programming adversity, syntax adversity is more closely linked to mathematics.

Syntax adversity was the least frequent type seen and consisted of the defining of variables in the program (S-00 – S-01), placement of code sequences (S-10 – S-19), and the structure of if statements and loops and their placement within the code (S-20 – S-29). All are closely linked to the logical and structural build of mathematical procedures, such as the simple multiplication before addition rule. Syntax adversities, when resolved (S-00 – S-01 and S-10 – S-19), were observed to facilitate an internal construction of the programming code and the understanding of each element and the relations between them (Verschaffel et al., 2020a). When the students resolved syntax adversities, they were observed to discuss and argue about the logical procedure of the program (S-10 – S-19). This construction and understanding were more evident when the sequential structure and knowledge of the mathematical task were explicit. In the task concerning the bisectional method, where the program incrementally calculated a better and better guess for the zero point, the students voiced arguments about the structure of the programming code. In the task concerning Newton’s method for finding the zero point, the students were observed to be less confident. The difference between the two was that all the steps involved in the bisectional method were known, while those in Newton’s method involved new configurations, such as the formula involving both the function and its derivative. The combined complexity of both new mathematics and new programming created two adversities to overcome, possibly generating an insurmountable barrier (Kirschner et al., 2006; Reiser, 2004).

The MPPs in which syntax adversities were minimal included well-known mathematical methods together with a design facilitating the transformation of the mathematical model into a model where the elements and their relation are essential for the solution (Verschaffel et al., 2020a). This indicates that when implementing programming in the mathematics classroom, it is better to apply it as a tool for deep learning when the mathematics has already been taught, rather than using it to introduce a new topic. Syntax adversities could also be alleviated by using a wider range of structural tools, such as flow diagrams and block charts, which have been shown to be good scaffolding tools for learning Python (Cabo, 2018).

Output adversities were as prominent as concept adversities but initiated a discussion over a longer time span and were observed to contain more mathematics, often combined with programming (O-10 – O-11 and O-20 – O-22). These kinds of adversities were resolved and therefore desirable (D’Mello & Graesser, 2014). When output adversities were not resolved within a reasonable time frame, the students effectively gave up and deleted the code causing the output adversity (O-30), making them disengage from the adidactical situation due to experiencing either an ontological or didactical obstacle (Brousseau, 1997) or an insurmountable understanding or information barrier (Ko et al., 2004). Like word problems, the programming tasks need to ensure scaffolding to facilitate the students’ ability to experiment and discuss the problem (Verschaffel et al., 2020b). As the design of the MPPs focused on building tasks allowing the students to explore, the number of unresolved output adversities was low (3 of 18). Output adversities are difficult to mitigate since they are hard to predict, and students have limited knowledge of how to interpret feedback from the editor. The output often becomes a problem-solving situation for the student (Polya, 1957), due to the, for them, irrational behaviour of the program (Ko et al., 2004). To circumvent this becoming an ontological obstacle, orchestrating a classroom conducive to the exploration of mathematical problem solving aids in maintaining an adidactical situation. This work reveals no direct way to prevent all output adversities, as the number of possible errors is numerous; however, teaching the students basic knowledge of how to handle errors was particularly advantageous.

Coding adversity is, for the mathematically inclined, perhaps the most interesting, where the advantage of combining mathematics and programming becomes visible. The typical sequence in coding adversity consists of the students exploring a mathematical problem or method, followed by how to solve the problem or implement the method into the program. The exploratory talk consisted of engagement (D-20 – D-21), suggestions for joint consideration (D-12, D-25), and justification (D-10 – D-15 and onwards), following the definition given by Mercer (2005). This element of exploratory talk is beneficial and contributes to learning (Mercer, 2005). The MPPs were built to take advantage of programming in mathematics using coding to solve a problem. Prior to their implementation in the mathematics classroom, tasks containing coding from mathematics to programming were viewed to be the most promising and were continuously added during the iterative design process. As seen in excerpt two from the coding adversities (D-10 – D-15), which shows the start of the discussion of the seemingly simple problem of making the program differentiate whether two numbers have the same or different signs, became a mathematical discussion lasting several minutes and eventually resulting in a short and simple code. The two main features of coding were to (1) use mathematics to make the program understand a simple mathematical relationship (as above), or (2) use mathematics to solve a complex problem through building a short program (bisectional method, Newton’s method). To avoid coding becoming an ontogenic obstacle, the students’ are building a mathematical model into converting the mathematical model to a programming model where the elements of the model and their relations are essential (Ko et al., 2004). Facilitating this building, the task provides scaffolding to the students through using and recalling previous mathematical knowledge required and guiding the students in their exploration of how to assemble a new mathematical and/or programming model (Kirschner et al., 2006; Reiser, 2004).

Concluding thoughts

Adversities when applying programming in the mathematics classroom are inevitable, as even coding experts encounter errors from time to time. The change from requiring a single input into a digital tool such as GeoGebra to building a program consisting of several lines of code is significant. The challenge for educators to reduce the adversities, in terms of both designing MPPs and orchestrating lessons, is substantial and needs further research. The work presented indicates several ways of reducing the number of adversities the students encounter and reflects on which should remain as part of mathematical learning. By scaffolding for the students in the design (Kirschner et al., 2006; Reiser, 2004) and orchestrating a classroom encouraging mathematical exploration (Mercer, 2005), these adversities can become valuable to learning. As regards designing MPPs, I would suggest care is taken to avoid building what could possibly become insurmountable barriers. Adversities should be predictable (Stein et al., 2008), as they are linked to the task design and therefore, to some extent, preventable. Further research into the affordances and constraints of implementing programming in the classroom is needed, especially studies spanning more than one class. As Niss (1999) stated, if we know the adversities that block the paths of students learning mathematics using programming, we will gain a better understanding of how mathematical knowledge and ability can be combined with programming, leading to better learning. Programming allows for mathematical investigation into many previously unavailable themes, such as numerical methods, as well as facilitating an in-depth learning of existing school mathematics, such as function analysis. To avoid the same fate as that seen the last time programming was implemented (Misfeldt & Ejsing-Duun, 2015; Papert, 1980), research into how it can facilitate mathematical learning is needed.