Demokrati og medborgerskap i matematikkundervisninga

Innleiing

Demokrati og medborgarskap er eitt av tre tverrfaglege tema som vart innført med læreplanverket for Kunnskapsløftet 2020 (LK20). Dei tverrfaglege temaa «tar utgangspunkt i aktuelle samfunnsutfordringer som krever engasjement og innsats fra enkeltmennesker og fellesskapet i lokalsamfunnet, nasjonalt og globalt» (Kunnskapsdepartementet, 2017, s. 12). I denne forskingsoversikta undersøker vi forskingsstudiar der temaet demokrati og medborgarskap er arbeidd med i matematikkundervisninga i skulen. Denne samankoplinga av demokrati, medborgarskap og matematikkundervisning kan sjåast på som ei delvis ny innramming av matematikkfaget. Tidlegare har matematikkfaget i lita grad blitt sett på som politisk orientert (Hannaford, 1998; Skovsmose, 1990), men som eit fag der elevane tileignar seg nøytral kunnskap (Alrø et al., 2010) gjennom å arbeide med lukka oppgåver som berre har eitt rett svar (Breivega et al., 2019).

Demokratisk utdanning er ikkje ein eksplisitt visjon i norsk skule, delvis grunna manglande samanheng mellom demokratisk teori og fagdidaktikk (Stray & Sætra, 2017). Det er eit gap mellom retningslinjer, teori og praksis som gjer det utfordrande for lærarar og lærarutdannarar i Noreg å implementere utdanning for demokrati og medborgarskap. Stray og Sætra (2017) meiner at ein sterkare samanheng mellom teori og praksis er mogleg. I denne artikkelen ønsker vi difor å undersøke koplingar mellom undervisning for demokrati og medborgarskap og matematisk kompetanse. Med utgangspunkt i empirisk forsking om arbeid med demokrati og medborgarskap i matematikkfaget, vil vi med denne artikkelen bidra til diskusjonen om korleis undervisning knytt til demokrati og medborgarskap kan realiserast i matematikkfaget i norsk skule. Vi har difor teke utgangspunkt i følgjande forskingsspørsmål:

• Kva seier matematikkdidaktisk forsking om arbeid med demokrati og medborgarskap i matematikkundervisninga?
• Korleis kan denne forskinga, i lys av litteratur om demokrati og medborgarskap, bidra til forståinga av det tverrfaglege temaet i matematikkfaget i norsk skule?

Vi startar med å teikne opp den teoretiske bakgrunnen for denne forskingsoversikta ved å først sjå på diskusjonen om demokrati og medborgarskap i norsk skule og vise til tidlegare forsking på temaet. Vi viser så kort korleis koplinga mellom demokrati og matematikkundervisning har utvikla seg dei siste tiåra. Deretter ser vi på demokrati og medborgarskap slik det er handsama i LK20 i lys av den presenterte litteraturen om temaet. Vidare gjer vi greie for den metodiske tilnærminga for arbeidet med denne forskingsoversikta. Til slutt presenterer og diskuterer vi resultata frå forskingsartiklane. Målet med artikkelen er å bidra til ei djupare forståing av kva arbeid med demokrati og medborgarskap i matematikkundervisninga kan vere.

Bakgrunn og tidlegare forsking

Demokrati og medborgarskap i skulen

Heldal og Sætra (2022) peikar på utfordringar knytt til demokrati og medborgarskap som tverrfagleg tema i skulen. For det fyrste handlar det om at kva demokratiforståing som blir lagt til grunn for undervisninga vil ha konsekvensar for kva slags demokrati- og medborgarskapsideal som blir styrka. For det andre handlar det om korleis ein skal implementere demokrati og medborgarskap i undervisninga. For det tredje handlar det om samanhengen mellom skulefaga og demokrati og medborgarskap som tverrfagleg tema, og om demokrati og medborgarskap skal knytast direkte til fagkunnskapen.

Basert på ulike medborgarideal i litteraturen om utdanning til demokratisk medborgarskap, presenterer Stray og Sætra (2019) tre idealtypiske forståingar av demokratiundervisning. Desse idealtypane har både ulikt innhald og ulik målsetjing. Den fyrste kallar dei utdanning til politisk informert medborgarskap. Her er målet å gi elevane den grunnleggande kunnskapen dei treng som informerte borgarar. Dette handlar om å bli ein informert politisk veljar gjennom å til dømes utforske politiske sakar og kva dei ulike partia meiner om desse, eller meir generelt om forståing og kunnskap om samfunnet. Det handlar altså om utdanning om og til representativt demokrati. Den andre kallar dei utdanning til rasjonelt autonomt medborgarskap. Denne har ei individualistisk orientering og handlar om å førebu elevar til å bli gode demokratiske borgarar i framtida. Dei må difor tileigne seg kunnskapar, ferdigheiter og haldningar som gjer dei i stand til å tenke kritisk og ta sjølvstendige val. Her handlar det såleis om utdanning for demokrati. Den tredje idealtypen kallar dei utdanning til sosialt intelligent medborgarskap. Denne handlar ikkje berre om demokrati i form av å velje sine leiarar, men også om å delta i og vere med på å forme demokratiet, og har såleis ei sosial orientering. Elevane skal lære å tenke og reflektere i samspel med andre. Demokrati er ikkje berre noko dei skal lære om for framtida, det er noko dei må få erfare og praktisere her og no. Såleis dreier det seg om utdanning for demokrati gjennom demokrati (Sætra & Stray, 2019).

Med utganspunkt i dei tre nemnde idealtypane har Sætra og Stray (2019) undersøkt kva slags medborgarideal som lærarar legg til grunn for demokratiopplæringa i skulen. Gjennom spørjeundersøkingar og kvalitative intervju fann dei at fleirtalet av lærarane i undersøkinga meiner at dei tre viktigaste måla for undervisning i demokrati og medborgarskap er å utvikle elevane si evne til kritisk tenking, å fremje kunnskap om demokratiske, politiske og samfunnsmessige institusjonar, og å utvikle elevane sine evner og ferdigheiter i konfliktløysing. Lærarane ønsker å utdanne for demokrati, og dette er eit mål som kan nåast hovudsakleg gjennom å hjelpe elevane med å tileigne seg kunnskapar (utdanning om demokrati) og evne til kritisk tenking. Lærarane i studien kommenterer i mindre grad utdanning til demokrati gjennom deltaking i sosiale praksisar i og utanfor klasserommet. Skulen skal gjere elevane til gode medborgarar i framtida, og blir såleis ein reiskap for demokratiet, i staden for at demokratiet er eit førebilete for skulen der elevane er medborgarar her og no (Sætra & Stray, 2019).

Westheimer og Kahne (2004) undersøkte to utdanningsprogram i USA som hadde mål om å fremje demokratiske verdiar. Det eine hadde fokus på den deltakande medborgaren. Dette utdanningsprogrammet hadde ei lokal orientering og elevane blei opplært til å bli deltakar i sitt lokale miljø. Den deltakande medborgaren er kjenneteikna av ei vilje og evne til å delta i fellesskapsorienterte tiltak i lokalmiljøet, som til dømes innsamling av klede til fattige. Det andre utdanningsprogrammet fokuserte på den rettferdsorienterte medborgaren. Dette utdanningsprogrammet reflekterer ei kritisk-pedagogisk tilnærming og søker sosial rettferd og evna til å analysere og stille spørsmål ved sosiale, økonomiske og politiske krefter og korleis desse verkar saman. Funna i studien viser at desse ulike utdanningsprogramma førte til at elevane utvikla ulike verdiar. Måten demokrati og medborgarskap blir tematisert på i undervisninga vil dermed påverke kva type medborgarar ein får.

Sett i samanheng med funna i Sætra og Stray (2019) si studie, kan dette bety at elevar lærer om demokrati og kritisk tenking, men får lite erfaring med å praktisere aktivt medborgarskap og delta i demokratiske praksisar. Dette får konsekvensar for kva type medborgar ein får fordi demokratikunnskapen til elevane har lite å bety for deira syn på seg sjølve som framtidige politisk aktive medborgarar (Ødegård & Svagård, 2018). Det som har størst innverknad, er å styrke elevane si politiske meistringstru. Ei slik meistringstru kan styrkast ved at undervisninga legg til rette for deltakande undervisningsformer (Ødegård & Svagård, 2018).

Matematikkundervisning og demokrati

Tradisjonelt har ikkje koplinga mellom matematikk og demokrati vore adressert eksplisitt i verken undervisning eller didaktisk forsking (Hannaford, 1998; Sætra og Stray, 2019). Skovsmose (1990) utfordrar denne tradisjonelle tankegangen og peikar på viktigheita av matematikk og matematisk kompetanse i eit demokratisk samfunn. På den eine sida dreier det seg om å utvikle ei forståing for korleis matematikken blir brukt i samfunnet, og dermed korleis matematikken formar samfunnet vi lever i. Dette blir omtalt som det sosiale argumentet for matematikk som demokratiserande kraft. På andre sida ligg det eit demokratiserande potensiale i måten matematikk blir undervist på – det pedagogiske argumentet. Skovsmose (1990) meiner at ein må vekk frå dei tradisjonelle rituala som ofte pregar matematikkundervisninga, der elevane primært lærer seg å følgje oppskrifter på korleis matematiske problem skal løysast. Denne måten å arbeide med matematikk på har lite til felles med korleis ein brukar matematikk i samfunnet elles. Ei anna side ved det pedagogiske argumentet handlar om at ein ikkje kan forvente at elevane skal utvikle demokratiske haldingar og kompetanse dersom skulesystemet og undervisninga ikkje tek i bruk demokratiske aktivitetar i undervisninga (Skovsmose, 1990).

Vidare utover 1990-tallet vart fleire forskarar interessert i denne koplinga mellom matematikk og demokrati (t.d. D’Ambrosio, 1990; Hannaford, 1998; Valero, 1999). Denne rørsla blei etter kvart omtalt som den sosiale vendinga, der ein var interessert i sosiokulturelle faktorar og korleis desse påverkar undervisning og læring i matematikk (Lerman, 2000). Døme på slike sosiokulturelle faktorar kan vere elevane sine kulturelle referanserammer, lærar–elev-relasjonar og samhandlingsmønster i klasserommet. Den sosiale vendinga har vorte vidareutvikla av fleire forskarar som no også er opptatt av å undersøke sosiopolitiske spørsmål knytt til matematikkundervisning i skulen gjennom å bruke sosiopolitiske teoriar og omgrep (t.d. autoritet, maktforhold, identitet og betydinga av sosioøkonomiske forhold) for å forstå og diskutere forholdet mellom faget, læreplanen, politikk og undervisning og læring (Bond & Chernoff, 2015; Gutiérrez, 2013).

Aguilar og Zavaleta (2012) har kartlagt forsking som kan plasserast innanfor den sosiale vendinga i matematikkdidaktikken. Grunnlaget for forskingsoversikta deira er artiklar i vitskaplege tidsskrift, konferanseartiklar og utvalde bøker som rapporterer om samanhengar mellom matematikkutdanning og demokrati. I sine funn trekker forfattarane fram tre samanhengar. Den første handlar om å gi elevane høve til å utvikle ein kritisk matematisk kompetanse; elevane skal kunne bruke matematikk til å forstå og analysere sosioøkonomiske problemstillingar og andre spørsmål som har personleg relevans for dei. Denne samanhengen kan relaterast til Skovsmose (1990) sitt sosiale argument. Den andre samanhengen, er at læraren legg til rette for utvikling av demokratiske verdiar og haldningar i undervisninga. Med eit fokus på læraren sine val av undervisnings- og læringsformer kan denne samanhengen relaterast til det pedagogiske argumentet til Skovsmose (1990). Til slutt viste forskingsoversikta at matematikkfaget kan fungere som ein «portvaktar», både for tilgang til (høgare) utdanning og for høvet til å delta i politiske diskusjonar der matematiske representasjonar blir brukte til å framstille sentrale poeng (Aguilar & Zavaleta, 2012). Døme på denne type diskusjonar kan vere økonomiske prioriteringar i politiske budsjett eller store internasjonale utfordringar slik som klimakrisa, behovet for omstilling til ei meir berekraftig energiforsyning eller måten vi som samfunn handterer pandemiar.

Med si forskingsoversikt viser Aguilar og Zavaleta, i tråd med Skovsmose (1990), at dei ulike argumenta for å sjå demokrati og matematikkundervisning i samanheng framleis er relevante, og at ein som lærar kan tematisere demokrati og medborgarskap både gjennom val av fagleg innhald og undervisnings- og arbeidsmåtar (Sætra & Stray, 2019). Med vår artikkel vil vi bygge vidare på arbeidet til Aguilar og Zavaleta (2012) med ei ny forskingsoversikt med eit eksplisitt fokus på empirisk forsking om arbeid med demokrati og medborgarskap i matematikkfaget i praksis.

Demokrati og medborgarskap i læreplanen

Med utgangspunkt i diskusjonane over, er det relevant å sjå nærare på kva type demokratiundervisning som er vektlagt i politiske styringsdokument for norsk skule. Fag – Fordypning – Forståelse — En fornyelse av Kunnskapsløftet (Meld. St. 28 (2015–2016)), er noko av grunnlaget for overordna del av LK20. Der står det at elevane må

tilegne seg kunnskap om demokrati og samfunnsdeltakelse og få øve på, erfare og praktisere demokratiske prosesser i praksis. Innholdet i det tverrfaglige temaet demokratisk medborgerskap kan blant annet være læring om demokratiet, læring for demokratisk deltakelse og læring gjennom demokratisk deltakelse. (Meld. St. 28 (2015–2016), s. 38)

Her er undervisning om, for og gjennom demokrati eksplisitt nemnt som noko det tverrfaglege temaet demokrati og medborgarskap kan innehalde. Ein kan dermed forvente at dei tre typane demokratiundervisning er å finne i LK20.

I skildringa av det tverrfaglege temaet demokrati og medborgarskap i overordna del av LK20, er det eksplisitt uttrykt at elevane skal få kunnskap om demokrati og demokratiske prosessar, og tema som ytringsfridom, stemmerett og organisasjonsfridom blir trekte fram. Dette kan relaterast til utdanning til politisk informert medborgarskap, eller utdanning om demokrati. Det blir også vist til utdanning til rasjonelt autonomt medborgarskap, utdanning for demokrati, ved at det blir peika på individet sine rettar og plikter i utforminga av det sivile samfunnet. Til slutt kan ein også finne argument for utdanning til sosialt intelligent medborgarskap, eller utdanning gjennom demokrati. Eit døme på dette er vektlegginga av at demokratiet må utviklast og haldast ved like, og at «skolen skal stimulere elevane til å bli aktive medborgarar og gi dei kompetanse til å delta i vidareutviklinga av demokratiet i Noreg» (Kunnskapsdepartementet, 2017). Opplæringa skal også gi elevane «ferdigheiter til å møte utfordringar i tråd med demokratiske prinsipp» og lære dei å «handtere meiningsbrytingar» (Kunnskapsdepartementet, 2017). Desse formuleringane kan innebere undervisning der elevane får gjere seg erfaringar ved å vere aktive og deltakande. På den andre sida blir ikkje erfaring og deltaking her og no, som Sætra og Stray (2019) vektlegg, eksplisitt nemnt i overordna del. Ein kan såleis også forstå formuleringane som noko elevane skal bli i stand til ein gong i framtida gjennom undervisning om og for demokrati. Undervisning gjennom demokratisk deltaking er difor ikkje like tydeleg forankra i overordna del av læreplanen som undervisning om og for demokrati.

Ser vi vidare på læreplanen i matematikk, kan vi lese at matematikkfaget skal gi elevane matematisk kompetanse slik at dei er førebudde på livet i samfunnet og arbeidslivet (Kunnskapsdepartementet, 2019). Under overskrifta «Fagrelevans og sentrale verdiar», blir det trekt fram at modellering og anvendingar er sentrale for å forstå samanhengar i samfunnet og naturen. I tillegg blir kritisk tenking, kommunikasjon, abstraksjon, generalisering og problemløysing nemnt som viktig i matematikkfaget. Arbeid med desse verdiane ska bidra til at elevane blir rusta til å gjere eigne val i livet sitt og i samfunnet. Ein kan her sjå parallellar til demokratiopplæringa som blir omtalt i overordna del av læreplanen når det i matematikkfaget blir vektlagt at elevane skal utvikle matematisk kompetanse som dei kan bruke i møte med samfunnet, og at dei skal kunne analysere og tenke kritisk om samanhengar i samfunnet og naturen. Verdiane i matematikkfaget, slik dei blir formulert her, er òg i tråd med ei undervisning for og gjennom demokrati, då dei legg vekt på at elevane skal utvikle kunnskapar og ferdigheiter som gjer dei i stand til å tenke kritisk og ta eigne val. Vidare er dei i tråd med det sosiale argumentet til Skovsmose (1990), som etterlyser matematikkundervisning som gir elevane høve til å forstå og analysere problem i samfunnet.

Viktigheita av dei sentrale verdiane blir vidare understreka av at ein kan kjenne dei att i faget sine kjerneelement. Læreplanen i matematikk inneheld seks kjerneelement som består av sentrale omgrep, metodar, tenkemåtar, kunnskapsområde og uttrykksformer. Desse kjerneelementa er utforsking og problemløysing, modellering og anvendingar, resonnering og argumentasjon, representasjon og kommunikasjon, abstraksjon og generalisering og matematiske kunnskapsområde (til dømes tal, algebra, geometri og statistikk).

Skildringa av det tverrfaglege temaet demokrati og medborgarskap i læreplanen for matematikk ser ut til å vektlegge undervisning for demokrati. Det blir fokusert på kompetanse til å analysere og vurdere data og modellar, slik at elevane skal bli i stand til å delta i samfunnsdebatten. Det er altså snakk om å utvikle individet si kritiske tenking og rasjonelle autonomi (Sætra & Stray, 2019). Elevane skal bli medvitne om «føresetnader og premissar for matematiske modellar som ligg til grunn for avgjerder i deira eige liv og i samfunnet» (Kunnskapsdepartementet, 2019), men det er ikkje noko som peikar i retning av at elevane sjølve skal erfare demokratiske prinsipp gjennom å vere aktive og deltakande. Det er altså samsvar mellom dei ulike delane av «Om faget» når det gjeld vektlegginga av samfunnsperspektivet og kritisk tenking i læreplanen i matematikk.

Om ein nyttar funksjonen «Støtte til læreplanen» på Utdanningsdirektoratet sine nettsider, får ein opp konkrete kompetansemål knytte til demokrati og medborgarskap. Desse kompetansemåla handlar i hovudsak om å lese, presentere og vurdere statistikk, og å nytte funksjonar i modellering av praktiske situasjonar. Her dreier det seg i stor grad om utdanning for demokrati, ved at elevane skal utvikle kritisk tenking, og forstå kva som ligg til grunn for statistikk og modellar dei kan møte i ulike situasjonar. I skildringa av demokrati og medborgarskap i læreplanen for matematikk er det såleis lite som kan knytast til undervisning om og gjennom demokrati.

Metode

Inspirert av Arksey og O’Malley (2005) og Creswell og Guetterman (2019) har vi utført forskingsoversikta etter følgjande fem steg: (1) Formulere forskingsspørsmålet og identifisere nøkkelomgrep innanfor det valde fagfeltet; (2) Identifisere relevante publikasjonar; (3) Kritisk utval av publikasjonar etter bestemte kriterium; (4) Systematisering, tolking og syntetisering av data; (5) Oppsummering og samanstilling av resultata.

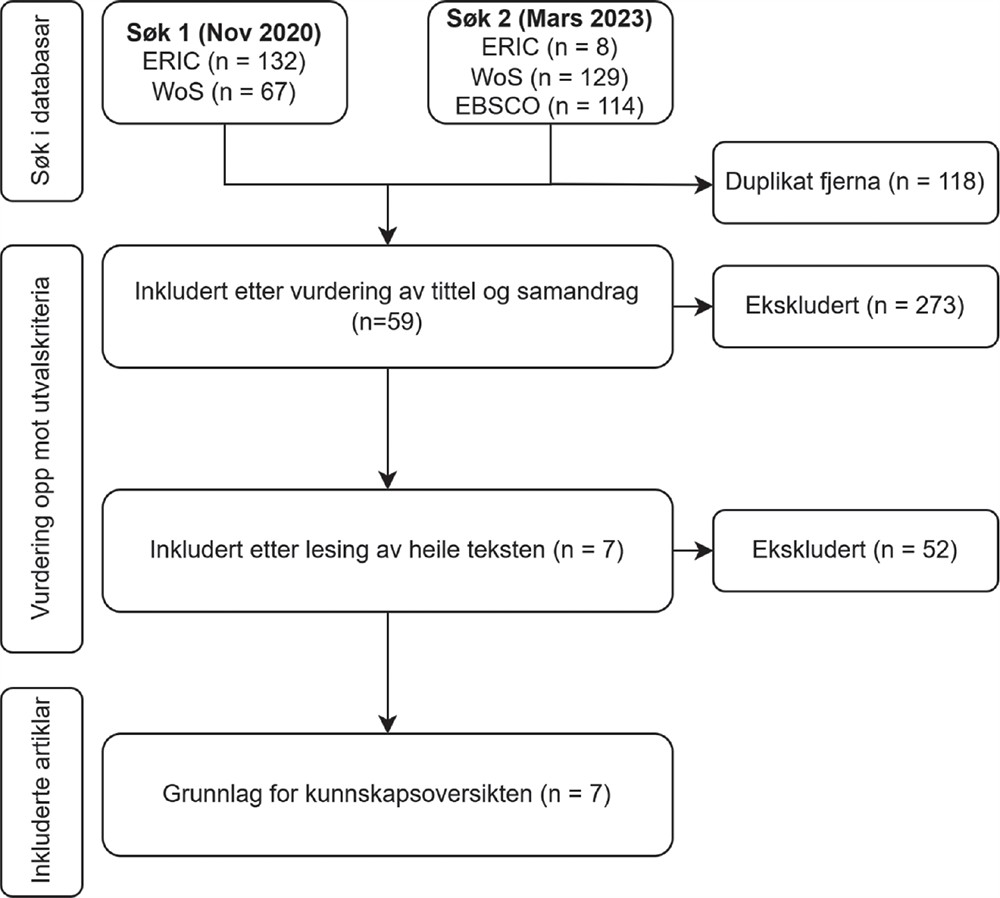
Steg ein starta då vi formulerte forskingsspørsmåla og byrja arbeidet med å førebu litteratursøket som ligg til grunn for forskingsoversikta. Litteratursøket blei gjennomført i to fasar. Den første fasen var eit fulltekstsøk i databasane ERIC og Web of Science som blei gjennomført i november 2020, og var ein del av arbeidet med masteroppgåva til førsteforfattaren (Olsson, 2021). Dette søket kan karakteriserast som eit preliminært søk (eng. scoping search) som har til hensikt å kartlegge og vurdere omfanget av litteraturen på eit bestemt forskingsområde (Booth et al., 2016). Søkefrasane som blei brukt var inspirert av den sosiale vendinga innan matematikkdidaktisk forsking (Lerman, 2000) og samansett av ulike kombinasjonar av «critical mathematics education», «mathematics education», «democracy», «citizenship», «emancipation» og «empowerment».

I fase to av søket, gjennomført i mars 2023, brukte vi ein søkestreng som er ei oppdatering av søkefrasane frå den første fasen: (”math* education” OR ”critical math*” OR CME) AND (democra* OR citizenship OR emancipat* OR empower* OR equit*). I fase to avgrensa vi søket til samandrag, samstundes som vi utvida søket til å inkludere databasen Academic Search Elite (EBSCO), i tillegg til ERIC og Web of Science. Vi valde desse tre databasane då vi vurderte dei til å gi god tilgang til internasjonal forsking innanfor humaniora og utdanningsvitskap. Steg tre i prosessen var å vurdere resultata av søka opp mot utvalskriteria (tabell 1). Bakgrunnen for val av publiseringsperiode var studien til Aguilar og Zavaleta (2012), som såg på artiklar publisert fram til 2012. Søket vårt var inspirert av Aguilar og Zevaleta (2012), men våre utvalskriterium var strengare med tanke på at vi berre var interesserte i empiriske studiar frå grunnskule og vidaregåande skule. Vi brukte dei same utvalskriteria i begge søka. Etter at vi hadde vurdert artiklane opp mot utvalskriteria sat vi igjen med sju artiklar – grunnlaget for denne forskingsoversikta. Søke- og utvalsprosessen er illustrert i figur 1. Tabell 3 viser ei oversikt over dei inkluderte artiklane.

Tabell 1. Utvalskriterium for litteratursøk

^a Grå litteratur er litteratur som ikkje er publisert i fagfellevurderte tidsskrift, til dømes rapportar frå konferansar utan fagfellevurdering, bøker og bokkapittel, studentoppgåver, doktorgradsarbeid og avisartiklar (Røkenes & Krumsvik, 2014).

I steg fire nytta vi ei deduktiv tilnærming når vi systematiserte, tolka og syntetiserte funna i artiklane. Vi konstruerte tematiske analysekategoriar med utgangspunkt i forskingsspørsmåla og litteraturen som utgjer bakgrunnen for denne artikkelen. Tabell 2 syner ei skjematisk oppsummering av analysearbeidet og kategoriane som vi brukte i dette arbeidet. Det femte og siste steget i prosessen blir gjort greie for i den påfølgande delen, der resultatet av litteraturgjennomgangen blir presentert og drøfta opp mot utvald didaktisk teori og tidlegare forsking.

Resultat og diskusjon

Tilnærming til demokratiundervisning

Demokratiundervisninga i skulen kan ta ulike former (Breivega et al., 2019; Heldal & Sætra, 2022; Westheimer & Kahne, 2004). Det er vanskeleg å sjå eit tydeleg skilje mellom ulike tilnærmingar til demokratiundervisning i dei inkluderte artiklane, men ein kan sjå at ulike sider ved demokratiundervisning er meir eller mindre vektlagde. Majoriteten av artiklane vi har sett på tek føre seg aktivitetar knytt til sosiopolitiske spørsmål (jf. tabell 2). Til dømes dreier det seg om problemstillingar knytte til miljø og klima (Brelias, 2014; Hauge & Barwell, 2017), diskriminering og marginaliserte grupper (Brelias, 2014; Oh & Kwon, 2014) og sosioøkonomiske spørsmål (Radakovic, 2015; Schell-Straub, 2013). Dette er døme på undervisning som følgjer det sosiale argumentet til Skovsmose (1990). Ein tydeleg trend er at når undervisninga tek utgangspunkt i sosiopolitiske spørsmål, så får elevane høve til å arbeide med ein kritisk matematisk kompetanse når dei skal analysere, vurdere og ta stilling til samfunnsmessige utfordringar.

Tabell 2. Skjematisk framstilling av analysen

Tabell 3. Oversikt over inkluderte artiklar

To artiklar (Hauge & Barwell, 2017; Schell-Straub, 2013) er av spesiell interesse, då dei viser døme på korleis ein både kan arbeide med undervisning for og gjennom demokrati. Hauge og Barwell (2017) viser døme på at ei sosiopolitisk problemstilling også kan ha direkte kulturell relevans for elevane. Dei skriv om korleis argument for og mot oljeleiting utanfor Lofoten blei brukt i eit tverrfagleg undervisningsopplegg, der matematikken hadde ei sentral rolle. Problemstillinga knytt til oljeleiting er eit allment sosiopolitisk spørsmål, samstundes som det er noko som elevane i studien har ei direkte tilknyting til, sidan havområdet utanfor Lofoten er ein del av deira nærmiljø. Elevane måtte nytte kunnskap og erfaringar knytt til nærmiljøet og matematikk for å formulere argument for og mot ei reell samfunnsmessig problemstilling. I undervisninga blei det fokusert på deltaking i diskusjonar der elevane skulle bruke matematikk til å formulere argument for å kunne delta i ein pågåande politisk diskusjon. Med vektlegginga av denne typen diskusjon og bruken av eit aktuelt politisk problem kan dette forståast som utdanning gjennom demokrati og eit døme som aktualiserer både det sosiale og det pedagogiske argumentet for demokratiundervisning i matematikkfaget.

Schell-Straub (2013) viser korleis matematisk modellering kan brukast i arbeid med sosiopolitiske spørsmål. Artikkelen skildrar eit tverrfagleg prosjekt der elevane fekk velje eit problem knytt til temaet fattigdom. Dei skulle deretter utvikle underspørsmål til temaet dei hadde valt, og finne kjelder som kunne gi svar på desse spørsmåla. Elevane brukte så eigne matematiske kompetansar til å analysere og tolke informasjonen dei fann, for så å samanfatte, gjerne med eigne modellar, og presentere resultata på ein plakat. Elevane fekk høve til å tolke og kritisk reflektere over det dei fann. Mellom anna diskuterte dei korleis det kunne ha seg at ein graf som viste at folketalet i eit slumområde minka, samstundes som talet på fattige auka. Elevane arbeidde altså med å utvikle modelleringskompetanse, samstundes som dei lærte om tema knytt til demokrati og medborgarskap. Denne studien viser korleis ein kan arbeide med undervisning gjennom demokratisk deltaking i matematikk. Schell-Straub (2013) argumenterer for at matematikkundervisninga kan gjerast rikare om den hentar inspirasjon frå demokratiske utdanningstradisjonar, særleg gjennom å invitere elevane til å vere delaktige i utforminga av undervisninga. Vi meiner at dette er eit godt døme på korleis eit undervisningsopplegg kan tematisere reelle samfunnsutfordringar, samstundes som elevane får arbeidd med sentralt matematikkfagleg innhald på ein kritisk måte, og får oppleve å kunne påverke korleis undervisninga blir gjennomført. Såleis vil denne tilnærminga til matematikkundervisning både adressere det sosiale og det pedagogiske argumentet til Skovsmose (1990) og vere i tråd med samanhengane mellom matematikk og demokrati som Aguilar og Zavaleta (2012) har identifisert.

Vi har også funne døme på undervisning der ein nyttar matematiske oppgåver der sjølve arbeidsmåten, og meir generelt dei pedagogiske tilnærmingane, kan koplast til demokrati og medborgarskap. I til dømes Lo og Ruef (2020) blir det vist til ein undervisningssekvens der elevane i fellesskap og gjennom diskusjon, fann fram til ein måte å rekne ut arealet til eit trapes. I tillegg til det matematikkfaglege, arbeidde lærarane aktivt for at elevane skulle bli bevisste si eiga rolle i gruppearbeidet og at dei skulle bidra til å anerkjenne kvarandre sine bidrag i arbeidet med å finne arealet av trapeset. Målet var at elevane skulle få erfaringar knytt til det å respektere, anerkjenne og forstå andre, og å dele og argumentere for sine eigne tenkjemåtar. Denne undervisninga kan relaterast til undervisning for demokratisk deltaking, då ein av målsetjingane er å utvikle elevane sine demokratiske verdiar og ferdigheiter.

Lo og Ruef (2020) sitt fokus på argumentasjon, samarbeid og diskusjon finn vi også att i studien til Safi et al. (2018). Hovudskiljet her er at undervisninga i Safi et al. (2018) tek utgangspunkt i eit samansett sosiopolitisk spørsmål: manipulering av valdistrikt (eng. gerrymandering). I dette opplegget arbeidde elevane med matematiske omgrep, som fordeling, likskap/ulikskap og areal, for å få ei betre forståing for «gerrymandering» som fenomen. Lo og Ruef (2020), Safi et al. (2018) og Schell-Straub (2013) syner at det er mogleg å arbeide med å utvikle demokratiske verdiar og haldingar hjå elevane både ved å arbeide med tradisjonelle matematiske tema og ved å trekke inn aktuelle sosiopolitiske spørsmål i undervisninga.

Matematikkfagleg innhald

I artiklane vi har sett på, kjem det tydeleg fram kva matematiske tema det blir arbeidd med og kva undervisnings- og arbeidsmåtar som blir brukt. Når vi ser desse matematiske temaa, undervisnings- og arbeidsmåtane i lys av den norske konteksten og LK20 er det mogleg å sjå at elevane arbeider med fleire kjerneelement. Vår analyse (samanfatta i tabell 2) syner at elevane i studiane arbeider med eitt eller fleire matematiske kunnskapsområde, samstundes som eitt eller fleire tema som kan knytast til dei andre kjerneelementa i den norske læreplanen blir tematisert. Alle dei inkluderte studiane syner såleis døme på korleis ein kan arbeide med demokrati og medborgarskap i matematikkfaget.

I undervisninga som er skildra i artiklane, ser vi at somme arbeidsmåtar går att. Desse er problemløysing, matematisk modellering, prosjektarbeid og diskusjon. Utforsking og problemløysing og modellering og anvendingar er to av kjerneelementa i læreplanen. Diskusjon kan relaterast til fleire kjerneelement. Til dømes ser vi diskusjon i samanheng med resonnering og argumentasjon, der elevane skal kunne følgje, vurdere og forstå matematiske tankerekker, og grunngi framgangsmåtar, resonnement og løysingar (Kunnskapsdepartementet, 2019). I tillegg ser vi diskusjon i samanheng med representasjon og kommunikasjon. Dette kjerneelementet handlar om ulike måtar å uttrykke matematiske samanhengar og omgrep på, og å kommunisere matematikk gjennom eigne erfaringar og matematiske samtalar (Kunnskapsdepartementet, 2019).

At desse arbeidsmåtane går att, kan tenkast å henge saman med at kontekstane for undervisninga som er skildra i artiklane ofte er knytt til sosiopolitiske spørsmål og at det er snakk om komplekse problemstillingar der løysinga ikkje er opplagt frå starten. Spørsmål om til dømes fattigdom og fordeling av økonomiske godar (Oh & Kwon, 2014; Schell-Straub, 2013), manipulering av valdistrikt (Safi et al., 2018) eller vurdering av risiko knytt til kjernekraft (Radakovic, 2015) er vanskeleg å finne enkle svar på, og i mange tilfelle må situasjonane både forenklast og abstraherast for at ein skal kunne nytte matematikk for å gi ei løysing på problemet. Slik sett vil elevane både måtte diskutere og bli einige om korleis denne typen problemstillingar skal tolkast og korleis dei skal kunne arbeide med matematikken bak utan å ha ein på førehand definert framgangsmåte. I matematisk modellering er det nettopp eit poeng at ein nyttar situasjonar frå den verkelege verda som utgangspunkt. Ein må beskrive eit problem frå dagleglivet matematisk, før ein tolkar det matematiske resultatet i lys av den opphavlege situasjonen. Problemløysing handlar om å løyse problem der ein ikkje har ein på førehand kjend løysingsmetode (sjå Kunnskapsdepartementet (2019) for skildring av matematisk modellering og problemløysing i læreplanen). Dette er ofte også tilfelle når ein står overfor eit problem i det verkelege livet. Såleis kan diskusjon, samarbeid, problemløysing og matematisk modellering vere hensiktsmessige arbeidsmåtar for å tilnærme seg denne typen sosiopolitiske spørsmål som blir arbeidd med i desse studiane.

Undervisninga som er omtalt av Schettino (2013) er eit godt døme på at elevane aktivt må forhandle og diskutere seg fram til svar på komplekse problemstillingar. I denne studien blir læringa og innhaldet i undervisninga utvikla av elevar og lærarar saman i eit diskusjonsbasert klasserom, med utgangspunkt i sosiopolitiske problemstillingar. Klasserommet skal vere eit ikkje-hierarkisk miljø der stemmene, erfaringane og forkunnskapane til elevane blir verdsette. Denne måten å arbeide på blir omtalt som relasjonell problembasert læring (Schettino, 2013). Også i andre studiar er elevane sine stemmer viktige i val av problemstillingar og arbeidsmåtar (Schell-Straub, 2013).

Arbeid med problemløysing blir nemnt av fleire (Brelias, 2014; Hauge & Barwell, 2017) utan at det blir gitt ei detaljert omtale av sjølve undervisninga eller arbeidsmetodane som er brukte. Safi et al. (2018) viser derimot døme på fleire problemløysingsoppgåver. Dette er opne oppgåver der elevane på førehand ikkje er kjend med ein løysingsmetode, som til dømes å finne ulike måtar å dele inn eit valdistrikt på for å påverke valresultatet. Her må elevane arbeide med problemløysingskompetanse ved at dei skal finne ulike løysingar på same problem. I tillegg må dei nytte resonneringskompetanse for å argumentere for dei matematiske vurderingane dei har gjort, til dømes i gruppering og regruppering i utforminga av valdistrikta.

I undervisningssekvensen som Lo og Ruef (2020) skildrar, arbeider elevane òg med problemløysing, då dei skal finne arealet til eit trapes utan at dei er kjent med formelen. Målet er å komme fram til og drøfte ulike strategiar for å finne arealet. Problemløysingskompetanse kan i dette tilfellet handle om å vurdere om dei ulike strategiane fører fram. Elevane kan òg arbeide med abstraksjon og generalisering ved å vurdere om strategiane er gyldige i alle tilfelle eller berre for dette spesifikke trapeset. Elevane samarbeider i grupper og vil dermed få bruk for både resonnerings- og kommunikasjonskompetanse når dei saman skal finne arealet til figuren. Til slutt er undervisningssekvensen kopla til det matematiske kunnskapsområdet geometri, ved at elevane arbeider med arealomgrepet.

Vi finn spor av modellering og anvendingar i fleire artiklar, sjølv om dei ikkje eksplisitt tek opp matematisk modellering eller modelleringskompetanse. Brelias (2014) studerer elevar si oppfatning av korleis matematikken kan brukast til å undersøke samfunnsmessige problem gjennom bruk av statistikk og matematisk modellering. Elevane skal bruke, reflektere over og vurdere matematikk knytt til ulike tema, som til dømes fordeling av ressursar i eit samfunn og finansiering av skulen. Resultata viser at elevane måtte revurdere sine tankar om matematikk. Dei erfarte at matematikk var eit viktig verktøy for å avsløre sosial urettferd, men at å bruke matematikk på denne måten ikkje var så uproblematisk og objektiv som dei fyrst trudde. Radakovic (2015) rapporterer om liknande funn. Han påpeikar at vurdering av statistiske modellar vil bli påverka av etiske og moralske vurderingar, og kan såleis ikkje forståast i eit vakuum. Ein treng også innsikt i andre fagdisiplinar for å kunne analysere komplekse sosiopolitiske spørsmål. Sidan elevane i desse studiane kritisk vurderer matematikk som er brukt for å beskrive og forklare reelle sosiopolitiske spørsmål, arbeider dei med å utvikle modelleringskompetanse, samstundes som dei arbeider med det matematiske kunnskapsområdet statistikk.

Diskusjon er ein sentral arbeidsmåte i fleire av studiane (Hauge & Barwell, 2017; Lo & Ruef, 2020; Oh & Kwon, 2014; Radakovic, 2015; Schettino, 2013). I Oh og Kwon (2014) skal elevane analysere og reflektere over tal og datasett som viser den skeive fordelinga av rikdom i verda. I dette arbeidet varierer ein mellom arbeid i grupper og felles klassediskusjon om resultata. I diskusjonen om trafikktryggleik i Hauge og Barwell (2017) må elevane argumentere for kva parameter dei må ta omsyn til og kor mange målingar dei treng for å utvikle ein modell for å vurdere trafikktryggleiken. Slike diskusjonar inneber også matematiske resonnement og argument, til dømes kva som vil vere føremålstenlege representasjonsformer og matematiske prosedyrar. På denne måten vil ein kunne komme inn på kjerneelementa resonnering og argumentasjon og representasjon og kommunikasjon.

Felles for studiane vi har sett på, er at dei fokuserer på undervisning for og gjennom demokrati. Det å nytte oppgåvekontekstar knytte til sosiopolitiske spørsmål, samfunnsmessige utfordringar og kulturelle kontekstar gjer at elevane må gjere seg opp ei meining om problemstillingar som er sentrale for ei demokratisk forståing. Elevane må òg nytte matematikk i formuleringa og vurderinga av argument og påstandar som blir lagde fram. Slike vurderingar kan til dømes kaste lys over korleis problemstillingane påverkar ulike samfunnsgrupper, og korleis matematikk kan nyttast for å overtyde, manipulere og forme meiningar om sosiale og politiske spørsmål. Såleis er dette døme på undervisning for demokrati. Fleire av arbeidsmåtane i studiane er døme på korleis ein kan legge opp undervisning gjennom demokratisk deltaking, då samarbeid, kommunikasjon og det å gi og ta ansvar blir ein del av matematikkundervisninga (t.d. Hauge & Barwell, 2017; Lo & Ruef, 2020). Til slutt er undervisningsaktivitetane knytte til ulike matematiske kunnskapsområde, med hovudvekt på statistikk.

Avslutning

I gjennomgangen av den overordna delen av LK20, synte vi at undervisning om og for demokrati var tydlegast framheva, men at ein også kan sjå spor av undervisning gjennom demokratisk deltaking. I læreplanen for matematikk ligg hovudvekta på undervisning for demokrati. Fokuset på undervisning for og gjennom demokrati går att i artiklane vi har sett på i denne forskingsoversikta. Undervisning om demokrati er ikkje vektlagt i verken matematikkplanen eller studiane vi har sett på. Det er ikkje overraskande, då denne typen demokratiundervisning gjerne ligg til andre fag, som samfunnsfag og KRLE.

Studiane vi har sett på viser at det finst mange moglegheiter for å arbeide med demokrati og medborgarskap i matematikkundervisninga. På den eine sida kan ein nytte Skovsmose (1990) sitt sosiale argument, og arbeide med sosiopolitiske spørsmål der elevane må bruke matematisk kunnskap når dei skal analysere ein situasjon og formulere argument for løysingane sine. Dette samsvarer med fagrelevans og sentrale verdiar i matematikk, slik det er formulert i LK20, med tanke på å førebu elevar på livet i samfunnet. Vårt syn er at denne førebuinga best skjer dersom elevane får arbeide med reelle problemstillingar som ikkje har enkle og eintydige svar. Det kan vere problemstillingar knytte til andre skulefag som gir moglegheit for tverrfaglege prosjekt, eller dagsaktuelle problemstillingar knytte til lokale, globale eller kulturelle tema.

Studiane syner òg at ein kan arbeide med undervisning for og gjennom demokrati ved å ta utgangspunkt i meir tradisjonelle matematiske oppgåver. Då handlar det om å utøve demokratiske prinsipp i klasserommet. For læraren kan denne samhandlinga gå ut på å gi frå seg noko autoritet for at elevane skal lære å dele sine tenkjemåtar, respektere, anerkjenne og forstå kvarande og utvikle eiga handlekraft. Dette samsvarer med det pedagogiske argumentet til Skovsmose (1990).

Ikkje alle dei matematiske temaa i kompetansemåla i LK20 er like lette å innlemme i meir opne sosiopolitiske problemstillingar. Ein kan også kjenne på at sjølve matematikken får for lite merksemd dersom undervisninga alltid skal ta utgangspunkt i sosiopolitiske problemstillingar. Mange vil argumentere for at matematikken også har ein verdi i seg sjølv – forfattarane av denne artikkelen inkludert – og at noko av det vakre og meiningsfulle med matematikk, nettopp er at den kan abstraherast og vere fri frå kontekst. Ved å forstå det tverrfaglege temaet demokrati og medborgarskap som samansett av undervisning om, for og gjennom demokrati, og sjå temaet i lys av både det sosiale og det pedagogiske argumentet til Skovsmose (1990), trur vi at matematikkundervisninga vil kunne bidra til å utvikle medborgarar som både kan tenke kritisk og handle, og samstundes halde fokus på dei aspekta som er særeigne for matematikkfaget. Desse særeigenskapane, slik vi ser det, handlar nettopp om denne tosidigheita: rolla matematikken spelar i samfunnet og naturen på den eine sida, og dei generelle og abstrakte samanhengane ein finn i matematikken som fagdisiplin på den andre.

I kompetansemåla i matematikk i LK20, er demokrati og medborgarskap i hovudsak knytt til kjerneelementa utforsking og problemløysing, modellering og anvendingar og matematiske kunnskapsområde (til dømes statistikk, sannsyn og funksjonar). Desse kjerneelementa og matematiske kunnskapsområda går også att i undervisningsaktivitetane i artiklane i denne forskingsoversikta. Vi har i denne artikkelen vist at demokrati og medborgarskap i matematikkundervisninga er meir enn det som kompetansemåla eksplisitt legg opp til. Ei snever tolking av kompetansemåla kan føre til at ein tek utgangpunkt i ein praktisk kontekst, men fokuserer på ein instrumentell bruk av matematikken. Eit døme på dette er tradisjonelle tekstoppgåver, der ein kjem fram til eit matematisk resultat, utan å ta vidare omsyn til sjølve konteksten. Difor vil læraren si forståing av kva undervisning for demokrati og medborgarskap er, ha stor betydning for korleis dette temaet blir arbeidd med i matematikkundervisninga. Vidare vil typen demokratiundervisning ha betydning for kva type medborgar ein får (jf. funna til Westheimer og Kahne, 2004).

Gjennom denne artikkelen har vi vist døme på at demokrati og medborgarskap kan forståast og arbeidast med på mange måtar. For å imøtekomme læreplanen sin intensjon om å utdanne elevar til medborgarar i eit demokratisk samfunn, må undervisninga innebere undervisning av demokrati og medborgarskap i vid forstand. Det handlar ikkje berre om å utvikle elevar sin matematiske kompetanse, men også auke kunnskapen deira om korleis bruken av matematikk har innverknad på verda rundt oss og korleis ein kan handle basert på denne kunnskapen. På denne måten kan elevane bli «endringsagentar», bidragsytarar og forkjemparar for eit meir rettferdig samfunn (Safi et al., 2018).

Arbeid med demokrati og medborgarskap i matematikkfaget kan bidra til kunnskap om kontekst og matematikkfagleg kunnskap på ein positiv og gjensidig måte (Radakovic, 2015). Likevel viser denne forskinsoversikta at det er forholdsvis få klasseromsstudiar som eksplisitt utforskar dette temaet. Eit resultat på 7 sju artiklar er eit relativt lite grunnlag å bygge ei forskingsoversikt på, noko som kan vere ei svakheit ved denne studien. Det låge talet artiklar er truleg eit resultat av dei strenge utvalskriteria, og særleg avgrensinga til å berre inkludere empiriske artiklar knytt til matematikkfaget i grunnskule og vidaregåande skule. Dersom vi til dømes hadde inkludert teoretiske artiklar og empiriske artiklar frå andre skulefag og høgare utdanning, ville talet truleg vore høgare. Det er også mogleg at andre eller fleire søkeord ville gitt andre og fleire resultat.

Det låge talet på aktuelle artiklar syner at det trengs meir forsking på korleis demokrati og medborgarskap i matematikkundervisninga praktisk kan sjå ut, og kva kunnskap og kompetanse slik undervisning er med på å fremje. Vidare forsking kan også sjå på moglegheiter for å arbeide med demokrati og medborgarskap og matematikk i eit større tverrfagleg perspektiv. Berre ein av dei inkluderte artiklane har utgangspunkt i den norske konteksten. Det er difor eit behov for forsking om undervisning av det tverrfaglege temaet demokrati og medborgarskap i matematikk i norske klasserom.