Læringsbane i matematikk – et planleggingsverktøy for undervisning

Bak en godt gjennomført undervisning ligger en godt planlagt undervisning. Læreren må være i forkant av det som skal og kan skje i klasserommet, og dette starter med god planlegging. Det finnes flere forskjellige planleggingsverktøy som lærere kan velg mellom, for eksempel den didaktiske relasjonsmodell og baklengs planlegging. Jeg skal her presentere planleggingsverktøyet læringsbane og knytte dette planleggingsverktøyet til faget matematikk. Presentasjonen av planleggingsverktøyet læringsbane i matematikk bygger på erfaringer jeg har gjort sammen med grunnskolelærerstudenter på 1–7. trinn.

Hva er god undervisning?

Matematikkundervisning har som mål å utvikle elevens forståelse, engasjement og evne til å beregne, anvende og resonnere i arbeid med matematikkoppgaver (Torkildsen, 2017). En grundig forberedt undervisningstime øker muligheten for at elevene oppnår kompetansemålet og læringsmålet for undervisningsøkten. Derfor er det viktig at læreren planlegger undervisningen godt.

Det å planlegge undervisning i matematikk omfatter mange elementer, og Klette (2013) har i sin studie gitt et overblikk over forskningen som har foregått innenfor temaet undervisning. Studien trekker fram tre prinsipper for god undervisning (Klette, 2013, s. 178): 1) undervisningssituasjonen, 2) relasjonskompetanse og klasseledelse og 3) læringsmiljø og planlegging av undervisningen. Her trekkes planlegging av undervisning fram som et av disse prinsippene, og hun fremhever betydningen av dette for god undervisning.

Eksempler på planleggingsverktøy

Det er mange hensyn og avgjørelser læreren må ta i planleggingen av matematikkundervisningen. Berggren og Jom (2021, s. 61) trekker fram noen viktige elementer i planleggingen av undervisning: 1) disponering av tiden, 2) struktur på timen, 3) hva skal læres?, 4) ekstra oppgaver og 5) avslutningen av timen.

Den didaktiske relasjonsmodellen er et planleggingsverktøy de fleste lærere har et forhold til når det gjelder planlegging av undervisning. Modellen inneholder seks elementer. Disse er: 1) elev- og lærerforutsetning, 2) mål, 3) rammefaktorer, 4) arbeidsmåter, 5) innhold og 6) vurdering (Bjørndal & Lieberg, 1978). Alle disse seks elementene påvirker og forholder seg til hverandre. Dette planleggingsverktøyet kan virke ganske omfattende å bruke, og en veldig forenklet modell som ofte brukes i hverdagen er: Hva skal læres, hvordan skal elevene lære det, og hvorfor skal elevene lære akkurat dette? (hva, hvordan, hvorfor).

Et annet planleggingsverktøy er baklengs planlegging (Wiggins & McTighe, 2005). Baklengs planlegging handler om at læreren tar utgangspunkt i kompetansemål og vurdering, og deretter planlegger undervisningen ut fra kompetansemål og hvordan man som lærer skal vurdere om elevene har oppnådd kompetansemålet. Dette planleggingsverktøyet legger vekt på tre elementer i planleggingen: 1) forventet læringsmål (mål), 2) dokumentere kompetansen (vurdering), og 3) planlegging av undervisningen.

Med planleggingsverktøyet baklengs planlegging starter læreren med å velge ett eller flere kompetansemål for undervisningen og bryter disse ned til læringsmål for timen (forventet læringsmål). Læringsmålet er hva eleven skal lære i løpet av undervisningen. For å vurdere om elevene har oppnådd læringsmålet, må læreren ha tenkt gjennom hvordan dette kan bli vurdert (dokumentere kompetansen). Etter at læringsmål og kriterier for vurderingen er bestemt, kan planleggingen av undervisningsøkten begynne. Her planlegger læreren strukturen på timen med blant annet hvilke oppgaver og aktiviteter elevene skal arbeide med.

Læringsbane i matematikk

Både den didaktiske relasjonsmodellen og baklengs planlegging er gode planleggingsverktøy, men jeg mener at disse planleggingsverktøyene mangler spesielt ett element: matematisk horisontkunnskap. Ball mfl. (2008) beskriver matematisk horisontkunnskap som kunnskap om hvordan de matematiske emnene i læreplanen er relatert til hverandre, og hvordan de utvikles videre i elevers utdanning. Jeg mener og tror at hvis en lærer har god matematisk horisontkunnskap, kan læreren se hvilke forkunnskaper elevene trenger for å arbeide med den aktuelle matematikken, og klare å velge oppgaver og aktiviteter som bygger på og forholder seg til det elevene har lært tidligere og hva de skal lære videre. Dette elementet, matematisk horisontkunnskap, mener jeg kommer godt fram i planleggingsverktøyet læringsbane i matematikk.

Læringsbane i matematikk har sitt utspring i hypotetiske læringsbaner som stammer fra et konstruktivistisk læringssyn. Ifølge Simon (1995, s. 135) er det «the teacher’s prediction as to the path by which learning might proceed». Oversatt og tolket ut fra norsk skole innebærer det lærerens antakelser om hvordan læring skjer med utgangspunkt i kompetansemål, læringsmål, læringsaktiviteter og den antatte læringsprosessen (Simon, 1995).

En læringsbane i matematikk må inneholde tre elementer: 1) et matematisk mål, 2) en bane eller sti som eleven følger for å oppnå det matematiske målet, en læringsbane, og 3) en rekke oppgaver og aktiviteter som gjør at eleven oppnår ny kunnskap for å nå det matematiske målet, en undervisningsbane (Clements & Samara, 2020). Det matematiske målet kommer fra kompetansemålene i LK20, og læringsbanen er den faglige banen eleven må gå. Undervisningsbanen handler om de oppgavene og aktivitetene som læreren velger at elevene skal arbeide med for å nå det matematiske målet, se figur 1.

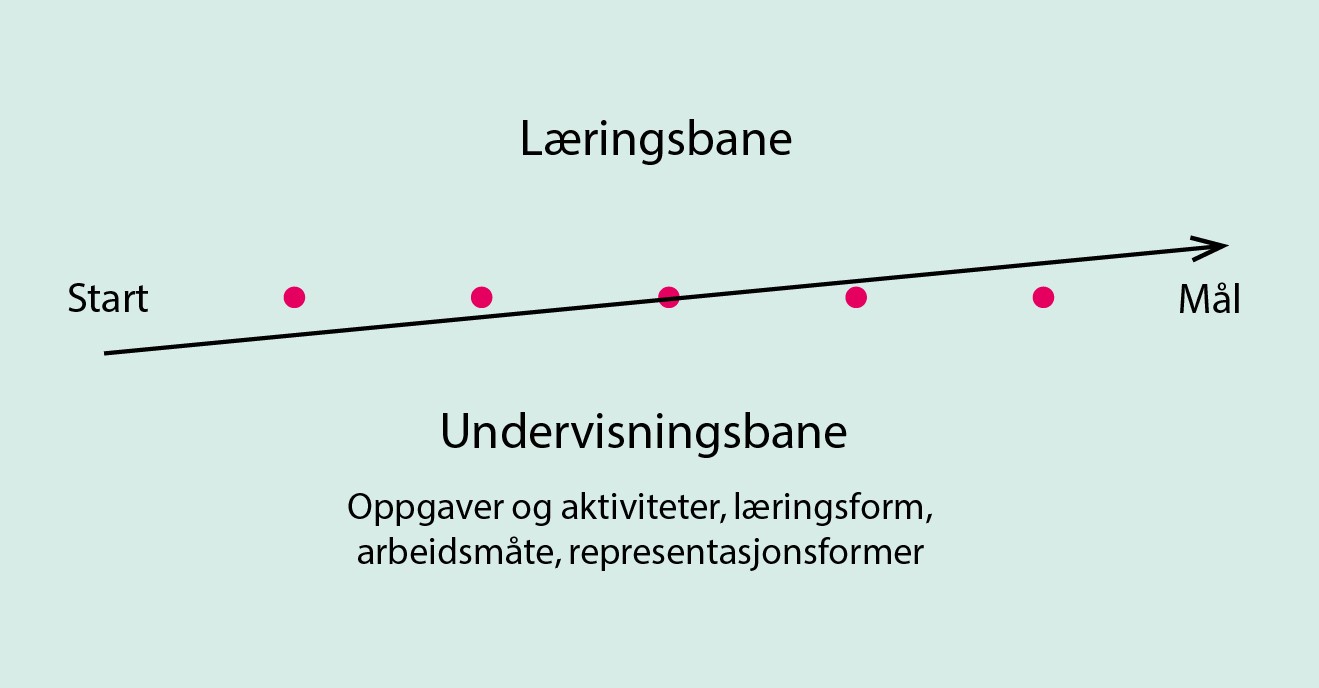
Figur 1 viser et generelt bilde av en læringsbane, men i denne figuren er det lagt til forslag om hva undervisningsbanen kan inneholde. I faget matematikk er det viktig at elevene får erfaring med å uttrykke matematikk på forskjellige måter, gjennom ulike representasjonsformer. I tillegg må læreren tenke gjennom hvilke oppgaver og aktiviteter elevene skal arbeide med, og hvordan elevene skal arbeide med disse oppgavene og aktivitetene. Med utgangspunkt i modellen til Clements og Samara (2020) har jeg utviklet et skjema som lærerstudentene kan bruke for å planlegge den undervisningen som skal gjennomføres. Punkter som er med i skjemaet er:

• Kompetansemål: Kompetansemålet eller kompetansemålene hentes fra LK20.
• Læringsmål (matematisk mål): Kompetansemålet brytes ned til læringsmål, hva elevene skal lære i matematikk i løpet av undervisningen.
• Kjerneelementer: Hvilke kjerneelement(er) er med i undervisningen?
• Grunnleggende ferdigheter: Hvilken grunnleggende ferdighet er med i undervisningen?
• Start: Hvilke forkunnskaper trenger eleven?
• Matematisk delmål: Hvilken matematikk må eleven bruke for å oppnå læringsmålet (matematisk mål)?
• Oppgaver og aktiviteter: Læreren velger ut hvilke oppgaver/aktiviteter elevene skal arbeide med for å oppnå læringsmålet (matematisk mål).
• Læringsform: Hvordan skal elevene arbeide for å tilegne seg den matematiske kunnskapen? Det er seks læringsformer elevene kan arbeide med: 1) tilegnelse, 2) undersøkelse, 3) diskusjon, ) øvelse, 5) produksjon, 6) samarbeid.
• Arbeidsmåte: Skal elevene arbeide individuelt, i par, i gruppe?
• Representasjonsformer: Hvordan skal elevene løse oppgaven? Det er fem representasjonsformer: 1) visuell, 2) fysisk, 3) kontekst, 4) verbal og 5) symbolsk.
• Struktur på timen: Hvordan er undervisningen planlagt?

Erfaringer med planleggingsverktøyet læringsbane i matematikk

Grunnskolelærerstudentene på 1.–7. trinn fikk i oppgave å lage et undervisningsopplegg om «beregning av areal til 2-dimensjonale figurer», og dette er en del av et kompetansemål på 6. trinn. Studentene ble delt i grupper på tre stykker, og alle gruppene satt i klasserommet og arbeidet. Etter at gruppene var ferdig med å lage et forslag til undervisningsopplegg om beregning av areal til 2D-figurer, gikk vi gjennom og diskuterte hvert punkt i skjemaet. Sammen fylte vi ut undervisningsopplegget «Beregning av areal til 2D-figurer», se tabell 1.

Tabell 1: Eksempel på utfylt skjema for læringsbane for beregning av areal til 2D-figurer

En læringsbane i matematikk må inneholde tre elementer: matematisk mål, læringsbane og undervisningsbane (Clements & Samara, 2020). Med utgangspunkt i den planlagte undervisningen om beregning av arealet til 2D-figurer er en figur av læringsbanen vist i figur 2. Figuren inneholder det matematiske målet, som er beregning av areal, det matematiske innholdet i læringsbanen og innholdet i undervisningsbanen.

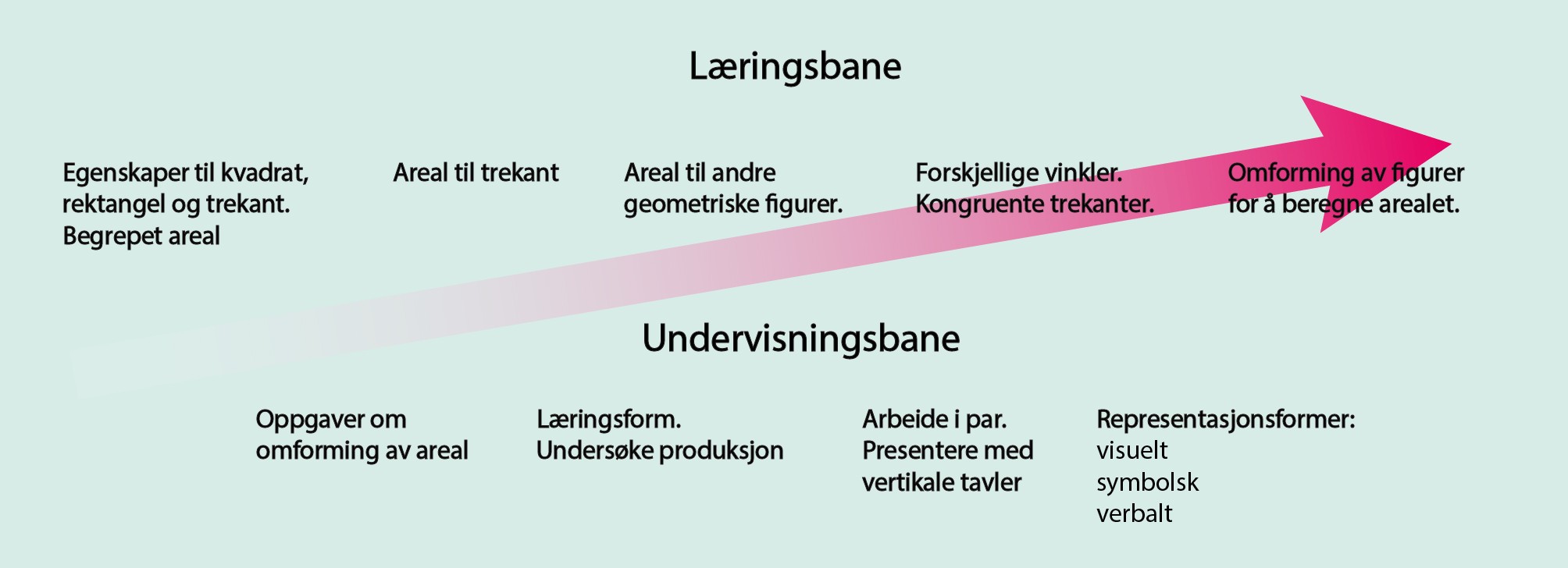
I undervisningen av læringsbane i matematikk med grunnskolelærerstudentene på 1.–7. trinn var det spesielt to områder som ble vektlagt. Det ene området var det å ta utgangspunkt i et kompetansemål og omformulere dette til et læringsmål. Det som var viktig her, var at læringsmålet var formulert på en slik måte at læreren kan vurdere om elevene har oppnådd læringsmålet (Stein & Smith, 2018, s. 17). Det andre området var det matematiske innholdet. Hvilke forkunnskaper i matematikk må elevene ha, og hvilken matematikk må elevene bruke for å oppnå læringsmålet?

Mine erfaringer med å undervise i bruk av planleggingsverktøyet læringsbaner i matematikk for grunnskolelærerstudenter på 1.–7. trinn, 1. og 3. trinn, viser til både muligheter og utfordringer. En av utfordringene var det å ta et kompetansemål og omformulere det til et læringsmål. Det å formulere læringsmål som var presise, og som i tillegg lot seg vurdere i løpet av undervisningen, var krevende. Studentene hadde liten erfaring med dette, så dette brukte vi tid på.

En annen utfordring var å la lærerstudentene arbeide med det matematiske innholdet i planleggingen av undervisning. De trengte trening i å se hvilke forkunnskaper elevene trenger, og hvilken matematikk elevene bruker når elevene løser oppgaver, det vi kaller matematisk horisontkunnskap.

Lærerstudentene hadde liten erfaring med å arbeide med matematikk på denne måten, men senere i semesteret observerte jeg flere studenter som ganske raskt så hvilket matematisk innhold de arbeidet med når de løste matematikkoppgaver.

Det å arbeide med horisontkunnskapen (Ball mfl., 2008) er et sentralt element i planleggingsverktøyet læringsbane i matematikk. Lærerstudenten må kjenne til den matematiske kunnskapen som trengs for at elevene skal kunne lære seg den «nye» matematikken, og læringsbanen er med på å gi lærerstudenten en oversikt og gjøre det lettere å se sammenhenger i de matematiske temaene i LK20.

En annen mulighet med læringsbane er at lærerstudenten får forankret den planlagte undervisningen i alle deler av LK20, som for eksempel kompetansemål, grunnleggende ferdigheter og kjerneelementer og dybdelæring. Dybdelæring i matematikk handler om at eleven skal anvende kunnskaper og ferdigheter på ulike måter, slik at eleven kan mestre ulike typer matematiske utfordringer individuelt og i samspill med andre (Kunnskapsdepartementet, 2017).

Tilbakemeldingene fra lærerstudentene på 1. trinn var blant annet at dette var et tidkrevende planleggingsverktøy å bruke, og at det var mange steg i planleggingsverktøyet. Positive tilbakemeldinger var at det ga læreren en god oversikt over hva elevene skal lære, og studentene så sammenhengen mellom den matematikken eleven skal lære, og alle deler av LK20: kompetansemål, kjerneelementer og grunnleggende ferdigheter.

Grunnskolelærerstudentene 1–7 på 3. trinn ga tilbakemelding om at dette var et godt verktøy, det var oversiktlig og hadde god struktur, noe som gjorde det enkelt å planlegge undervisningen. Noen lærerstudenter ga også tilbakemelding om at de fikk gått i dybden på matematikken som skulle undervises. Begge trinn ga også tilbakemelding om at dette var et planleggingsverktøy som fungerte i praksis. At 3.-trinnsstudentene var mer positive til planleggingsverktøyet, var ikke så overraskende. Disse studentene har fått mer erfaring fra praksis i løpet av lærerutdanningen, og de har erfart at et godt planlagt undervisningsopplegg ofte gir god matematikkundervisning.