Matematikklæreres refleksjoner om egne undervisningsutfordringer

Innledning

Matematikkundervisning stiller lærere overfor en rekke faglige utfordringer; i denne artikkelen omtaler vi disse utfordringene som «undervisningsutfordringer». Eksempler på slike undervisningsutfordringer er å presentere et matematisk problem, eller å knytte representasjoner til underliggende matematiske ideer (se ellers tabell 1). Dette er undervisningsutfordringer som alle matematikklærere jevnlig stilles overfor i undervisningen. Slike undervisningsutfordringer stiller krav til lærernes faglige, fagdidaktiske og pedagogiske kunnskap (jf. Shulman, 1986).

Forskere har identifisert en rekke matematiske undervisningsutfordringer som de mener undervisningsarbeidet består av (f.eks. Ball et al., 2008; Delaney, 2008), og disse undervisningsutfordringene har vært sentrale i utviklingen av tester og måleinstrumenter av undervisningskunnskap i matematikk (jf. Hoover et al., 2014). Måleinstrumentene er blant annet nyttige som konkretiseringer av hvordan kunnskapen kan se ut, men samtidig vil en teoretisk test som gjennomføres av lærerne utenfor undervisningssituasjonen miste noe av fokuset på det dynamiske og situasjonsbetingede ved undervisningsarbeidet (Ball, 2017). For å komme tettere på dette dynamiske arbeidet, har en del forskere studert de matematiske utfordringene slik de kan oppstå i selve undervisningen – ofte med utgangspunkt i egen undervisningspraksis (f.eks. Ball, 2017; Lampert, 2001). Slike studier har gitt ny og verdifull innsikt i hvordan de matematiske undervisningsutfordringene kan oppstå og møtes i undervisningen. En mulig svakhet med disse studiene er at de ofte er utført av forskere som studerer egen undervisning, og disse forskerne er allerede i utgangspunktet opptatt av å identifisere undervisningsutfordringene og de matematiske kunnskapskravene de fordrer. Et spørsmål en kan stille seg i møte med for eksempel studiene til Ball (2017) og Lampert (2001), er hvorvidt «vanlige» lærere er like bevisste på de matematiske undervisningsutfordringene de står overfor i undervisningsarbeidet og hvilke kunnskapskrav slike undervisningsutfordringer stiller. I denne studien analyserer vi hvilke matematiske undervisningsutfordringer som trer fram når lærere diskuterer egen undervisning, og vi diskuterer hvilke deler av den profesjonelle kunnskapsbasen lærerne selv trekker inn når de diskuterer ulike undervisningsutfordringer knyttet til egen undervisningspraksis.

Teoretisk bakgrunn

Etter flere tiår hvor forskerne var opptatt av å finne sammenhenger mellom undervisningsprosessen og elevenes læring, rettet Shulman (1986) oppmerksomheten mot faginnholdets rolle i undervisningen. I kjølvannet av Shulman har en lang rekke studier undersøkt ulike aspekter ved undervisningskunnskap i matematikk (for en oversikt, se Hoover et al., 2016). Disse studiene har tatt utgangspunkt i ulike problemstillinger (Ball, 2017). Mange har studert hvilken kunnskap lærere har og hvordan denne kunnskapen påvirker kvaliteten på undervisning og elevers læring (f.eks. Baumert et al., 2010; Hill et al., 2012). Andre har hatt fokus på den kunnskapen lærere bruker. For eksempel utviklet Rowland et al. (2005) rammeverket «Kunnskapskvartetten» gjennom analyser av hvordan lærerstudenter brukte matematisk kunnskap i undervisningen. I senere tid har Carrillo-Yañez et al. (2018) utviklet en annen modell for den matematiske kunnskapen lærere bruker i undervisningen. I likhet med Kunnskapskvartetten ble også denne modellen utviklet fra induktive analyser av observert kunnskap i bruk.

Studien som presenteres i denne artikkelen, tilhører en annen tradisjon hvor fokuset er på de kravene undervisningsarbeidet stiller. Denne tradisjonen tar utgangspunkt i den praksisbaserte teorien om «undervisningskunnskap i matematikk» til Ball et al. (2008) – på norsk ofte forkortet UKM (Fauskanger et al., 2010). I vår studie brukes UKM som operasjonalisering av den profesjonelle kunnskapsbasen. Mens andre forskere observerte hvordan lærere brukte ulike typer kunnskap i undervisningen, startet Ball og hennes kollegaer med å konseptualisere det matematiske undervisningsarbeidet lærere blir stilt overfor. Ball og Bass (2003) beskrev tilnærmingen som en «job analysis». Forskningen tok utgangspunkt i spørsmålene om hvilke gjentakende oppgaver og utfordringer lærere møter i matematikkundervisningen og hvilke matematiske kunnskaper og ferdigheter som kreves for å ta hånd om disse oppgavene (Ball et al., 2008). UKM er dermed tett knyttet til undervisningsarbeidets krav, og de matematiske undervisningsutfordringene blir sett på som en konkretisering av undervisningsarbeidet (Ball & Forzani, 2009).

Basert på omfattende analyser av det matematiske undervisningsarbeidet, ble en liste over de mest sentrale matematiske undervisningsutfordringene som lærere blir stilt overfor, identifisert (se tabell 1). Den praksisbaserte teorien om UKM ble så organisert rundt disse. «Allmenn fagkunnskap» ble beskrevet som matematisk kunnskap som ikke er unik for undervisningsarbeidet (Ball et al., 2008). Et eksempel er å finne verdien av summen 20 + 4. «Spesialisert fagkunnskap» er derimot en type matematisk kunnskap som er mer spesifikt knyttet til matematikkundervisning. Mens alle med allmenn fagkunnskap kan finne at 20 + 4 = 24, krever arbeidet med denne oppgaven i undervisningen at lærere kan vurdere gyldigheten til ulike løsningsmetoder og regnefortellinger. Dette er et eksempel på en faglig kunnskap som er spesifikt knyttet til de kravene undervisningen stiller. Den matematiske utfordringen er her knyttet til undervisningsarbeidet og ikke til det å løse selve oppgaven (Ball et al., 2008). Når lærere fokuserer på utvikling av gode hoderegningsstrategier hos elevene, brukes mengdeverdi ved at tallet 24 gjøres om til 20 + 4. Kolonneverdi handler om oppdeling i tiere og enere: 24 kan deles opp i to tiere og fire enere eller én tier og 14 enere, og dette er viktig i forhold til bruk av skriftlige (standard) algoritmer (Thompson, 2003). Forståelse for plassverdisystemet utgjør en felles kunnskapsbase som lærere trenger for å utføre arbeidet knyttet til denne oppgaven, og matematikklæreres profesjonsspråk kan på dette området inneholde vitenskapelige begreper som mengde- og kolonneverdi (Thompson, 2003).

Tabell 1. Matematiske undervisningsutfordringer.

«Tasks of teaching» (Ball et al., 2008, s. 400)	«Undervisningsarbeidets [matematiske] utfordringer» (basert på Fauskanger et al., 2010, s. 104)
Presenting mathematical ideas	Presentere matematiske ideer
Responding to students’ «why» questions	Respondere på elevers «hvorfor»-spørsmål
Finding an example to make a specific mathematical point	Finne eksempler for å få fram et bestemt matematisk poeng
Recognizing what is involved in using a particular representation	Være klar over hva som involveres når en bestemt representasjon tas i bruk
Linking representations to underlying ideas and to other representations	Knytte representasjoner til underliggende ideer og til andre representasjoner
Connecting a topic being taught to topics from prior or future years	Knytte emnet en underviser i, til emner fra tidligere år eller kommende år
Explaining mathematical goals and purposes to parents	Forklare matematiske mål og hensikter til foreldre/foresatte
Appraising and adapting the mathematical content of textbooks	Vurdere og tilpasse det matematiske innholdet i lærebøker
Modifying tasks to be either easier or harder	Endre oppgaver slik at de blir mer eller mindre utfordrende
Evaluating the plausibility of students’ claims (often quickly)	Vurdere om elevers påstander er rimelige (ofte raskt)
Giving or evaluating mathematical explanations	Gi eller evaluere matematiske forklaringer
Choosing and developing useable definitions	Velge og utvikle gode definisjoner
Using mathematical notation and language and critiquing its use	Bruke matematisk notasjon og språk, og bedømme bruken
Asking productive mathematical questions	Stille fruktbare matematiske spørsmål
Selecting representations for particular purposes	Velge hensiktsmessige representasjoner
Inspecting equivalencies	Undersøke likheter

En tredje komponent av UKM er «matematisk horisontkunnskap», som er «an awareness of how mathematical topics are related over the span of mathematics included in the curriculum» (Ball et al., 2008, s. 403). Eksempelvis kan læreres horisontkunnskap i eksemplet om oppdeling av tallet 24 være at de kan dele opp større flersifrede tall og skrive dem på standardform. Det kan også være å dele opp 24 i én tier og 14 enere som er nødvendig kunnskap for å utføre standard algoritme for subtraksjon. Samlet sett kan allmenn fagkunnskap, spesialisert fagkunnskap og matematisk horisontkunnskap ses på som en utvidet og mer spesifisert beskrivelse av det Shulman (1986) opprinnelig kalte «subject matter knowledge» (SMK).

Den andre av Shulmans (1986) hovedkategorier av lærerkunnskap er «pedagogical content knowledge» (PCK), og dette kan oversettes til matematikkdidaktisk kunnskap på norsk (Fauskanger et al., 2010). Ball et al. (2008) deler matematikkdidaktisk kunnskap i tre underkategorier. Den første, «kunnskap om faglig innhold og elever», er knyttet til elevers tenking og læring av et bestemt fagstoff. Et eksempel er kunnskap om vanlige misoppfatninger om posisjonssystemet (eksempelvis at standard oppdeling er det eneste riktige, at 24 kun kan deles opp som 20 + 4 og ikke som 10 + 14). Jones et al. (1996) har utviklet et rammeverk for plassverdi som beskriver hvordan elever tilegner seg kunnskap om tosifrede tall; dette kan også knyttes til «kunnskap om faglig innhold og elever». Rammeverket består av fem ulike nivåer fra pre-plassverdi til essensiell plassverdi. På hvert nivå er de fire sentrale begrepene telling, oppdeling, gruppering og tallrelasjoner beskrevet. Innenfor telling inkluderes å telle med én av gangen, med 10 og 100 av gangen forlengs og baklengs. Oppdeling av et tosifret tall som 24, kan for eksempel bety at tallet består av to tiere og fire enere, men også av én tier og 14 enere. Gruppering kan bety å gruppere i femmere eller tiere for å anslå en mengde og se verdien av slik gruppering, og med tallrelasjoner menes at eleven ser at 22 er mindre enn 24 og eventuelt hvor mye mindre. Lærerne i Jones et al. (1996) sin studie mente at kunnskap om disse sentrale begrepene utvidet deres perspektiver for undervisningsarbeidet knyttet til flersifrede tall, og i så måte kan rammeverket til Jones et al. (1996) være av betydning knyttet til «kunnskap om faglig innhold og elever» (Ball et al., 2008). McIntosh et al. (1992) har utviklet en modell for grunnleggende tallforståelse. I modellen inngår plassverdi, å ha tierpotenser som referanse, bruk av ulike representasjoner for tall samt det å gjenkjenne relativ og absolutt størrelse på en mengde som komponenter knyttet til kunnskap om tall. Modellen kan hjelpe lærere å analysere elevenes ulike svar på oppgaver av typen «Dagens tall» (se figur 1) og kan slik knyttes til «kunnskap om faglig innhold og elever» (Ball et al., 2008). For at elever skal forstå regneoperasjonene, må de forstå effekten av dem, de må kjenne til matematiske egenskaper som kommutativitet, og de må forstå sammenhengen mellom regneoperasjoner – eksempelvis addisjon og multiplikasjon. Når lærere skal undersøke om elever kan anvende kunnskap om tall, ser de om elevene ser sammenhengen mellom en kontekst og hvilken regneoperasjon som kan benyttes og om elevene benytter ulike strategier og framgangsmåter (McIntosh et al., 1992).

Den andre underkategorien av PCK er «kunnskap om faglig innhold og undervisning» (Ball et al., 2008), som innbefatter den matematiske kunnskapen lærere trenger i planlegging, gjennomføring og vurdering av undervisning. For eksempel må lærere velge ut eksempler og oppgaver og rekkefølgen på dem, og de må vurdere fordeler og ulemper med ulike representasjonsmåter og ulike undervisningsmetoder. Den siste kunnskapskomponenten i UKM-rammeverket er «Læreplankunnskap». Den omfatter blant annet kunnskap om hvordan de ulike emnene i læreplanen er relatert til hverandre, og også hvilke læremidler læreren vil benytte i undervisningen. I eksemplet med den åpne oppgaven om tallet 24 kan det bety å forstå hvilke kompetansemål fra læreplanen man arbeider med ved å benytte denne oppgaven.

I tillegg til matematisk og matematikkdidaktisk kunnskap, regner vi med at pedagogisk kunnskap (PK) også er en del av matematikklæreres felles kunnskapsbase (jf. Shulman, 1986). Dette omfatter mer generell profesjonskunnskap om elever, undervisning, læreplanarbeid og klasseledelse.

Med dette som utgangspunkt, retter vi oppmerksomheten mot følgende forskningsspørsmål:

1. Hvilke undervisningsutfordringer er i fokus når lærere reflekterer over egen matematikkundervisning?
2. Hvilke deler av den profesjonelle kunnskapsbasen trekker lærere inn når de diskuterer ulike undervisningsutfordringer?

Vi forsøker å svare på spørsmålene med utgangspunkt i en gruppe matematikklæreres refleksjoner om undervisningsarbeidet knyttet til en åpen oppgave om tallet 24.

Metode

Denne studien er en del av et større skolebasert forsknings- og utviklingsprosjekt. Deltakerne i studien er fire lærere som underviser på andre trinn i en norsk skole. Tre av lærerne er allmennlærere med utdanning i matematikk/matematikkdidaktikk på henholdsvis 30 og 15 studiepoeng, og én er førskolelærer med tilleggsutdanning på 30 studiepoeng i matematikk/matematikkdidaktikk. Alle fire har arbeidet som lærere i minst ni år. I studien er lærerne gitt fiktive navn: Anne, Berit, Carl og Doris.

Denne artikkelens førsteforfatter har veiledet (og studert) de fire lærerne i planlegging av undervisning, observert deres undervisning, samlet inn datamateriale fra elevenes arbeid med matematikk, samt diskutert med lærerne i etterkant av undervisningen. Forskningssamarbeidet startet med at lærerne deltok i et halvdags etterutdanningskurs hvor oppgaver som inviterer elever til diskusjon og til å benytte ulike løsningsstrategier (heretter kalt «åpne oppgaver») ble vektlagt. Lærerne har gjennom etterutdanningen blitt presentert for nyere matematikkdidaktiske forskningsresultater om matematikkundervisning, og de har diskutert og prøvd ut aktiviteter i egne klasser. Av temaene nevnes matematiske samtaler, utforskende arbeidsmåter og rike og åpne oppgaver. Når undervisningen omhandlet tallbegrep og tallverdi, ble flere av begrepene fra litteraturen brukt av både lærerne og kursholder (Thompson, 2003; McIntosh et al., 1992; Jones et al., 1996). Vi kan anta at dette vil ha innvirkning på svarene lærerne ga i gruppeintervjuet. Lærerne prøvde ut bruk av åpne oppgaver i klassene, og figur 1 viser et eksempel på andreklassingers respons på en slik oppgave hvor tallet 24 er i fokus (Maugesten et al., 2018). Oppgaven gitt til elevene var å skrive alt de kunne om dagens tall (24).

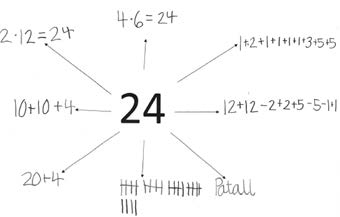
Etter at lærerne hadde prøvd ut denne åpne oppgaven med elevene, ble det gjennomført et semistrukturert gruppeintervju som varte en time. Begrunnelsen for å bruke gruppeintervju var at lærerne sammen kunne reflektere rundt en oppgave som de hadde planlagt og brukt i egen klasse. I et gruppeintervju vil interaksjonen mellom deltakerne kunne bidra til å avdekke enda flere refleksjoner (Kvale & Brinkmann, 2015). De fire lærerne ble i forkant av intervjuet invitert til å reflektere over hvorfor de valgte oppgaven, hva de ville oppnå med den og hvilke faglige utfordringer de møtte i planlegging og undervisning, samt hva slags matematisk/matematikkdidaktisk kunnskap de mente kreves i undervisningsarbeidet knyttet til oppgaven. Elevenes responser på oppgaven «Dagens tall er 24» er tidligere analysert (Maugesten et al., 2018), og disse responsene ble også diskutert i intervjuet. Transkripsjoner fra gruppeintervjuet utgjør datamaterialet analysert her.

Datamaterialet ble analysert ved hjelp av teoridrevet innholdsanalyse (Fauskanger & Mosvold, 2014; Hsieh & Shannon, 2005). I denne tilnærmingen anvendes koder fra teori og tidligere forskning deduktivt. Resultatene fra en teoridrevet innholdsanalyse kan da støtte opp under eksisterende teori, eller utfordre og videreutvikle denne (Hsieh & Shannon, 2005). Av alle lærernes utsagn (n=158) var 60 utsagn korte oppklarende spørsmål, ja- eller nei-svar, bekreftelser av tidligere utsagn og snakk som omhandlet andre ting enn undervisningen knyttet til oppgaven. De 98 resterende utsagna kodet vi først hver for oss ved bruk av de 16 matematiske undervisningsutfordringene som presenteres av Ball et al. (2008) (se tabell 1). Lærerne hadde ikke blitt presentert for de matematiske undervisningsutfordringene i etterutdanningsforløpet, men når temaet er matematikkundervisning, regnet vi med at flere av undervisningsutfordringene implisitt ville komme til uttrykk. Analysene kan derfor gi indikasjoner på hvordan lærernes refleksjoner rundt arbeidet med en åpen oppgave kan knyttes til det forskerne har identifisert som matematiske undervisningsutfordringer. Hvert utsagn ble gitt en kode etter hvilken (matematiske) undervisningsutfordring som kunne identifiseres i utsagnet. Kodingen var her åpen og inkluderende. For eksempel ble utsagnet «Også er det en åpen oppgave, så den er tilpasset alle ulike nivåer, alle kan få til et eller annet på en sånn oppgave da» i denne fasen av analyseprosessen kodet som et utsagn som potensielt kan knyttes til den matematiske undervisningsutfordringen å endre oppgaver slik at de blir mer eller mindre utfordrende.

Under kodingsprosessen så vi noen få eksempler på at et utsagn kunne plasseres under ulike matematiske undervisningsutfordringer.

Jeg begynner jo alltid å tenke litt sånn; Hva får jeg av utfordringer med denne oppgaven? Hvor kan det bli vanskelig for elevene, og hvordan kan jeg på en måte gi dem mestringsfølelse? Så der synes jeg det var fint at det fantes staver, tier-staver for eksempel, og ikke bare enere, for da tror jeg det hadde blitt vanskelig for noen. (Carl)

Dette utsagnet ble kodet som endre oppgaver slik at de blir mer/mindre utfordrende. Vi diskuterte om utsagnet også passet under undervisningsutfordringen å velge hensiktsmessige representasjoner fordi Carl snakket om ulike representasjoner, blant annet konkreter (stavene). Utfordringer og mestringsfølelse handler ikke bare om ulike representasjoner, men også om mulig endring av oppgaven med å stille spørsmål og formulere oppgaven på ulike måter. Det som avgjorde vårt valg av kode, var at det lå mer enn representasjoner i utsagnet. I en norsk undersøkelse der erfarne matematikklærere diskuterte lærerarbeidets matematiske undervisningsutfordringer, ble det argumentert for at flere av undervisningsutfordringene var vanskelig å skille fra hverandre (Fauskanger & Mosvold, 2016).

Neste steg i analysearbeidet var å kode hvert av de 98 utsagna i forhold til kategoriene i den matematiske kunnskapsbasen. Her tok vi utgangspunkt i Ball et al. (2008) sin modell for undervisningskunnskap i matematikk og brukte de seks kategoriene modellen er delt inn i. Poenget her var å indikere hvilke deler av kunnskapsbasen det kunne se ut til at lærerne trakk inn i refleksjonene. Artikkelens førsteforfatter gjennomførte en første runde med koding av utsagn. Artikkelens to andre forfattere gikk gjennom det første kodingsarbeidet hver for seg, og der vi var uenige diskuterte vi oss fram til enighet. Kodene vi brukte kan være overlappende, og derfor har vi en ekstra kategori der utsagn kan tilhøre to ulike kategorier i tabell 3 og 4.

Resultater og diskusjoner

I denne delen presenterer vi først resultater fra analysene av hvilke matematiske undervisningsutfordringer som er i fokus når lærerne reflekterer over egen matematikkundervisning. Deretter presenterer vi resultater fra analysene av hvilke deler av den profesjonelle kunnskapsbasen lærerne ser ut til å knytte til diskusjoner relatert til de ulike undervisningsutfordringene.

Matematiske undervisningsutfordringer i lærernes refleksjoner

Utsagn fra lærernes refleksjoner over egen matematikkundervisning fordelte seg på undervisningsutfordringene som vist i tabell 2. De fire nederste utfordringene i tabellen viste seg å ikke være relevante i denne studien.

Tabell 2. Antall utsagn som kan knyttes til de matematiske undervisningsutfordringene i tabell 1.

Lærerarbeidets matematiske undervisningsutfordringer	Ant.
Vurdere om elevers påstander er rimelige (ofte raskt)	21
Være klar over hva som involveres når en bestemt representasjon tas i bruk	15
Finne eksempler for å få fram et bestemt matematisk poeng	11
Endre oppgaver slik at de blir mer eller mindre utfordrende	10
Stille fruktbare matematiske spørsmål	9
Velge hensiktsmessige representasjoner	9
Gi eller evaluere matematiske forklaringer	6
Bruke matematisk notasjon/språk, og bedømme bruken	6
Knytte emnet en underviser i, til emner fra tidligere eller kommende år	5
Knytte representasjoner til underliggende ideer og til andre representasjoner	4
Presentere matematiske ideer	1
Velge og utvikle gode matematiske definisjoner	1
Respondere på elevers «hvorfor»-spørsmål	0
Forklare matematiske mål og hensikter til foreldre/foresatte	0
Vurdere og tilpasse det matematiske innholdet i lærebøker	0
Undersøke likheter	0
Totalt	98

Den matematiske undervisningsutfordringen lærerne reflekterer mest over når de diskuterer oppgaven om tallet 24, er å vurdere om elevers påstander er rimelige. Mange av refleksjonene omkring denne undervisningsutfordringen er knyttet til det matematiske innholdet. Et eksempel er når intervjueren stiller et spørsmål om hva eleven som har svart slik som i figur 2 kan. Berit svarer da at eleven «vet at sifferet 2 står for … har verdien 20, vet at sifferet 4 har verdien 4. Vet at sifferet 2 står på tierplass, og 4 på enerplass».

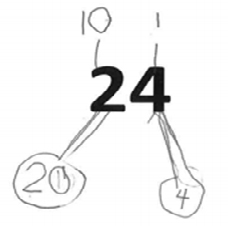
Berits respons kan tyde på at hun vurderer elevens matematiske forståelse knyttet til responsen vedkommende har gitt på oppgaven, og både mengde- og kolonneverdi (Thompson, 2003) trekkes fram. Selv om begrepene mengde- og kolonneverdi ikke brukes av Berit, er det klart at hun vektlegger mengdeverdi når hun sier at eleven «vet at sifferet 2 står for … har verdien 20, vet at sifferet 4 har verdien 4» og at hun vektlegger kolonneverdi når hun framhever at eleven vet at «sifferet 2 står på tierplass, og 4 på enerplass». Dette siste utsagnet kan også knyttes til det sentrale begrepet «oppdeling» (Jones et al., 1996), men igjen bruker ikke lærerne dette begrepet eksplisitt. I intervjuet får lærerne anledning til å vurdere elevenes respons i etterkant av undervisningsøkten, men i undervisningen må de gjøre dette på stående fot. Der og da kan det være krevende å forstå hvordan elevene tenker, noe som også kommer fram i intervjuet: «Jeg tror ofte at man kan se mer ting i ettertid, fordi at jeg opplever jo av og til at jeg kan liksom lure på hvordan elevene har tenkt. At jeg ikke alltid skjønner hvordan de har gjort det.» (Anne) Intervjuer følger opp med å spørre om læreren da stiller spørsmål til elevene, hvorpå læreren fortsetter:

Og ta fram litt mer sånn hvordan elevene tenker. Jeg har begynt å bli mye flinkere til å spørre dem om det, og [har] gjort det en stund, og etter at også du kom inn i bildet her, spørre dem «Hva tenkte du?», «Hvordan kom du fram til det?» Få dem til å prate litt mer. Snakke mye mer matematikk enn kanskje jeg gjorde tidligere, men også litt det derre med feilene og bruke mer tid på feilene.

Denne refleksjonen kan knyttes til undervisningsutfordringen å stille fruktbare matematiske spørsmål. Når Anne sier at hun vil «ta fram litt mer sånn hvordan elevene tenker» og at hun har «gjort det en stund», tolker vi dette som refleksjon over betydningen av å stille spørsmål som får fram elevenes matematiske tenking, samt egen erfaring med å få elevene «til å prate litt mer», til å «snakke mye mer matematikk [med elevene] enn kanskje jeg gjorde tidligere».

En annen undervisningsutfordring som lærerne reflekterte mye over, var å være klar over hva som involveres når en bestemt representasjon tas i bruk. Et eksempel er tatt fra en diskusjon om bruk av konkretiseringsmateriell i forbindelse med oppgaven knyttet til tallet 24:

Carl: Jeg holdt jo igjen tier-staver på noen som jeg vet om som klarer å jobbe med 24 stykker. Da fikk de ikke tier-staver og det var da de begynte å gruppere 6 og 6, 4 og 4, så begynte det å gå opp et lys for noen. Så de tier-stavene var det kanskje noen av de svake elevene som benyttet seg av i begynnelsen.

Berit: Samme med meg i forhold til ener-staver og tier-staver. Det er for å få på plass tallforståelsen opp til hundre.

I matematikkundervisningen framstilles matematiske ideer på ulike måter, og lærere må være klar over hva som er involvert når de bruker ulike representasjoner eller konkretiseringsmateriell. Carl vil at elevene skal gruppere og dele opp på annen måte enn kun med enere og tiere. Ved å gi elevene bare enere kan de for eksempel gruppere i sekser-grupper og i firer-grupper. Selv om Carl ikke bruker begrepene telling, gruppering og oppdeling, kan utsagnet knyttes til sentrale begreper i Jones et al. (1996) sitt rammeverk for plassverdi på ulike nivåer. Elevene får mulighet til å prøve en annen type gruppering enn gruppering i tiere og enere, slik Berit lar sine elever gruppere. I refleksjonene over ser vi også at Carl knytter dette til elevenes nivå.

En annen undervisningsutfordring som forekommer hyppig i refleksjonene, og som også handler om tilpasning, er å endre oppgaver slik at de blir mer/mindre utfordrende. Et eksempel var da Carl og Berit diskuterte valget av tallet 24:

Carl: Vi hadde jo tenkt å velge et lavere tall først, tror jeg. Men så syntes vi jo vel at det … men så begynte vi å tenke litt sånn i delbarheten at vi … jeg syntes ikke at det var …

Berit: Vi valgte egentlig i utgangspunktet et oddetall, men så … (...)

Berit: Vi jobbet jo med hva slags type tall vi skulle ha, hvor høyt skulle det være, hvor langt skulle det være, hvor mye kan elevene si om tallet, ikke bare lage regnestykker og utvidet form og alt dette her, men også om det er partall … Jobbe jo sånn at tallet vi skulle bruke, kunne brukes på mange forskjellige måter da. For hvis det er en faglig …

I: (avbryter med spørsmål) Er det derfor dere gikk bort fra å bruke oddetall, at dere valgte et partall isteden? 24?

Berit: Tror det var en av årsakene.

Anne: Så var det en av årsakene at 24 var delelig på 4.

I utdragene får vi innblikk i både Annes, Berits og Carls begrunnelser for valget av tallet 24. Tallet 24 i elevenes oppgave er ikke tilfeldig valgt; dette er noe lærerne har diskutert. De hadde først valgt et oddetall (Berit), men med tanke på delelighet ble de enige om å ha et partall i stedet (Carl, Anne). Lærerne ser ut til å ha et matematikkfaglig mål med oppgaven. De argumenterer med bruk av begrepene delelighet og partall, samt «å kunne bruke tallet på mange forskjellige måter» og et flersifret tall (omtalt som et «langt tall»).

Tilknytning til den profesjonelle kunnskapsbasen

I andre runde av analysen kodet vi hvilke deler av kunnskapsbasen lærerne ser ut til å trekke inn når de diskuterer de ulike undervisningsutfordringene. Da Ball et al. (2008) presenterte sin liste over matematiske undervisningsutfordringer, var poenget at dette var undervisningsutfordringer som stilte krav til lærernes matematiske og matematikkdidaktiske kunnskap. Et eksempel er å vurdere om elevers påstander er rimelige. Dette er en undervisningsutfordring lærere ofte møter i undervisningsarbeidet, og den stiller krav til en matematisk kunnskap som er spesielt knyttet til matematikkundervisningen. Når lærerne diskuterer besvarelsen til en elev som har skrevet 20 under 2-tallet og 4 ned fra 4-tallet (figur 2), så kommenterer Berit at dette indikerer at eleven «vet at sifferet (...) har verdien tjue, vet at sifferet 4 har verdien 4. Vet at sifferet 2 står på tierplass og 4 på enerplass». Dette illustrerer hvordan denne matematiske undervisningsutfordringen stiller krav til en type matematisk kunnskap som går utover det å finne riktig svar. Det å finne eksempler for å få fram et bestemt matematisk poeng er også en undervisningsutfordring som stiller krav til en type matematisk kunnskap som er spesifikk for undervisningsarbeidet. Et eksempel på dette ser vi når Anne peker på «at 24 var delelig på 4» som en av årsakene til at de valgte nettopp tallet 24 og ikke for eksempel et oddetall.

Tabell 3. Matematikkfaglig fokus i lærernes utsagn.

Matematisk fokus	Eksempler	Undervisningsutfordring
Spesialisert fagkunnskap (n=5)	«Vet at sifferet 2 står for ... har verdien tjue, vet at sifferet 4 har verdien 4. Vet at sifferet 2 står på tierplass, og 4 på enerplass» (Berit)	Vurdere om elevers påstander er rimelige
Allmenn fagkunnskap (n=14)	«Hvordan bruker man 2-tallet, hvordan bruker man 4-tallet. Hvordan bruker man 2- og 4-tallet til sammen, og så … De får vise mange flere sider enn det vi lærere kanskje ser. For vi kanskje, tenker mye tiere, vi tenker mye enere, men så kan vi begynne å dele det opp i flere hauger eller klasser ...» (Carl)	Vurdere om elevers påstander er rimelige
Allmenn/spesialisert fagkunnskap (n=2)	«Så var den en av årsakene at 24 var delelig på 4» (Anne)	Finne eksempler for å få fram et bestemt matematisk poeng
Horisontkunnskap (n=0)

Når vi ser nærmere på det matematikkfaglige fokuset i lærernes refleksjoner (jf. tabell 3), er det interessant å merke seg at selv om lærerne ser ut til å trekke inn allmenn fagkunnskap oftest (i 14 av 98 utsagn), er det også flere tilfeller hvor de har fokus på spesialisert fagkunnskap. Eksempler på dette er lærernes diskusjon av elevsvar på oppgaven, og av egenskaper ved posisjonssystemet. Følgende refleksjon fra Doris i en liknende oppgave illustrerer dette:

Jeg hadde jo noen elever som skrev 17 i stedet for 71 … at du da gjør tallrekken helt annerledes hvis du ikke har lov til å bytte 10-erene over på enerplassen eller motsatt for da lager du et helt annet tall … at verdien blir enten mindre eller større.

I dette utsagnet indikerer Doris at det ikke bare handler om å finne et svar, men å se hvordan svaret knyttes til egenskaper ved posisjonssystemet. Her ser vi klare indikasjoner på en felles kunnskapsbase, men lærerne bruker ikke presise vitenskapelige begreper. I Jones et al. (1996) beskrives elevenes utvikling av forståelse for posisjonssystemet med telling, oppdeling, gruppering og tallrelasjoner. I tillegg vektlegges fem ulike nivåer i utvikling av plassverdisystem.

Når lærerne i den videre diskusjonen av elevsvar blir spurt om hvorfor det er en god løsning å markere verdien av både 2-tallet og 4-tallet – samt å markere tiere og enere (figur 2) – sier Berit at det er «viktig å vite at sifferets plassering, hvilken verdi har det at … hva står sifferet 7 for i 73? Hva slags verdi har det?». Anne følger opp og sier:

For hvis du liksom klarer det fint, å dele det fra hverandre i tiergrupper og energrupper, så er det mye lettere å addere dem med andre tall også. Hvis du klarer å holde … at hvis du skjønner systemet, at det liksom sitter. At hvor mye er det tallet verdt, sifferet verdt? Hvilken plass står det på? Da er det jo mye enklere å addere med store tall og sånn også.

Her peker lærerne på at tallet 24 er delt opp i enere og tiere, og de er bevisste på hva verdien av sifferet på tierplassen er. Vi ser derimot ikke tegn til at lærerne bruker mer presise vitenskapelige begreper knyttet til for eksempel kolonne- og mengdeverdi (Thompson, 2003) i sine refleksjoner. Begge disse aspektene er sentrale i henholdsvis skriftlige algoritmer og hoderegning. Selv om lærerne ikke bruker disse begrepene direkte, ser vi indikasjoner på at de kjenner til begrepenes innhold.

Mange utsagn som er kodet som SMK har en relativt svak betoning av matematikken. Et eksempel er når Carl sier: «Vi hadde jo tenkt å velge et lavere tall først, tror jeg. Men så synes vi jo vel at det … men så begynte vi å tenke litt sånn i delbarheten.» Det at han nevner «delbarhet» indikerer et matematisk fokus, men dette blir ikke utdypet videre. Berit avbryter Carl med å si at de først hadde tenkt å bruke et oddetall. Selv om det matematiske ikke blir utdypet her, anser vi fokuset på tallets delelighet som en indikasjon på et matematisk fokus som går utover det en kan forvente av «allmennheten». Likevel ser vi ikke tegn til mer eksplisitte beskrivelser av de matematiske resonnementene som ligger til grunn.

14 av de 21 utsagna som er kodet som matematikkfaglig kunnskap er knyttet til allmenn fagkunnskap. Et eksempel på dette er Carls refleksjon rundt sifrene i tallet 24: «Hvordan bruker man 2-tallet, hvordan bruker man 4-tallet. Hvordan bruker man 2- og 4-tallet til sammen, og så … De får vise mange flere sider enn det vi lærere kanskje ser. For vi kanskje, tenker mye tiere, vi tenker mye enere, men så kan vi begynne å dele det opp i flere hauger eller klasser ...» Her kommer det matematiske fokuset tydelig fram, men andre utsagn som kan knyttes til allmenn fagkunnskap har et mindre tydelig fokus på matematikken.

En del av de matematiske undervisningsutfordringene kan også stille krav til fagdidaktisk kunnskap. I tabell 4 har vi illustrert hvordan det å vurdere om elevers påstander er rimelige kan stille krav til spesialisert matematisk kunnskap, men denne undervisningsutfordringen kan også stille krav til kunnskap om faglig innhold og elever. Et eksempel på dette ser vi når Anne kommenterer at mange elever skriver tallet på utvidet form, og at «det er veldig sånn fint å se hvor langt de har kommet i utviklingen i forhold til tallforståelsen». Et annet eksempel er å være klar over hva som involveres når en bestemt representasjon tas i bruk. Dette er en matematisk undervisningsutfordring som kan stille krav til spesialisert matematisk kunnskap, men den kan også stille krav til ulike aspekter ved fagdidaktisk kunnskap. Et eksempel på dette er Carls refleksjon over bruk av tierstaver. Da han unnlot å la noen av elevene få bruke tierstaver, observerte han at de begynte å sortere i grupper på seks og fire. «Så de tierstavene var det kanskje noen av de svake elevene som benyttet seg av i begynnelsen.» Dette utsnittet illustrerer hvordan denne undervisningsutfordringen kan stille krav til kunnskap om faglig innhold og undervisning og kunnskap om faglig innhold og elever.

Tabell 4. Fagdidaktisk fokus i lærernes utsagn.

Fagdidaktisk fokus	Eksempler	Undervisningsutfordring
Kunnskap om faglig innhold og elever (n=24)	«Det er veldig sånn fint å se hvor langt de har kommet i utviklingen i forhold til tallforståelsen» (Anne)	Vurdere om elevers påstander er rimelige
Kunnskap om faglig innhold og undervisning (n=17)	«Så teller vi mye [i undervisningen], veldig mye og vi begynner i rekken, teller hver tiende fra 3, så er det tretten, tjuetre, trettitre, førtitre. Hver tiende fra 7» (Berit)	Være klar over hva som involveres når en bestemt representasjon tas i bruk
Kunnskap om faglig innhold og både elever og undervisning (n=5)	«Jeg holdt jo igjen tierstaver på noen som jeg vet om som klarer å jobbe med 24 stykker. Da fikk de ikke tierstaver og det var da de begynte å gruppere 6 og 6, 4 og 4, så begynte det å gå opp et lys for noen. Så de tierstavene var det kanskje noen av de svake elevene som benyttet seg av i begynnelsen» (Carl)	Være klar over hva som involveres når en bestemt representasjon tas i bruk
Kunnskap om faglig innhold og læreplan (n=2)	«Rest hadde vi ikke hatt så mye av, for eksempel» (Carl)	Knytte emnet en underviser i til emner fra tidligere eller kommende år
Kunnskap om faglig innhold og både elever og læreplan (n=2)	«Ja, jeg har tre hauger og i hver haug er det 8 stykker. [Imiterer elev]. 3 ganger 8, sier de» (Carl)	Knytte emnet en underviser i til emner fra tidligere eller kommende år

Når refleksjonene kodet som fagdidaktiske studeres i dybden, finner vi at over halvparten (50 av 98 utsagn) har et uklart matematisk fokus. Et eksempel på dette er når Berit skal begrunne valget av oppgaven og sier: «Gikk jo mye på tallforståelse, at det er utviklingen av tallforståelse da». Her viser hun til tallforståelse, men verken hun eller kollegaene presiserer hva de legger i dette begrepet. Tallforståelse omtales som noe enkelte elever har kommet langt i, mens andre ikke har kommet så langt (Anne), og vi ser ingen spor av henvisninger til for eksempel McIntosh et al. (1992) sin modell der både kunnskap om tall, regneoperasjoner og anvendelse er inkludert i begrepet tallforståelse. Fagbegreper blir i liten grad tydeliggjort og utdypet. Slik mangel på tydeliggjøring og presisjon kan tolkes på flere måter. En mulig tolkning er at det eksisterer en felles profesjonell forståelse på dette området, og at det derfor er unødvendig for lærergruppen med presisjon når de diskuterer. En annen mulighet er at dette kan tolkes som taus kunnskap som lærerne ikke er i stand til å uttrykke med presise begreper. En tredje mulig tolkning er at mangelen på presise fagbegreper i refleksjonene indikerer at lærerne ikke har slike presise begreper. Til denne muligheten må vi ta med at lærerne ikke ble spurt om å tydeliggjøre fagbegreper i intervjuet fordi de der skulle reflektere rundt egen undervisning og oppgaven om tallet 24.

I noen av utsagna kodet som fagdidaktisk kunnskap er det matematiske fokuset noe sterkere. For eksempel ser lærerne ut til å være bevisste på posisjonssystemets betydning i arbeidet med oppgaven. Et av Berit sine utsagn illustrerer et fokus på kunnskap om faglig innhold og undervisning:

Men jeg har brukt … jeg har brukt … ja, jobba mye med tallforståelse og posisjonssystemet, hva er en ener, hva er en tier, tegnet opp på … eller skrevet tallrekken opp på ti og fortsatt videre med 11 … og har begynt med … at de får en hel tier. Først har de fått 9 enere, så har de fått en ener til og så har vi snakket om en tier-stav og så har de fått en tier. Så de har hatt det konkret foran seg.

Her blir faguttrykk noe mer tydeliggjort enn i eksemplene ovenfor. Berit beskriver her gruppering i tiere, overgang mellom tiere og plassverdi, men hun bruker ikke de mer formelle begrepene fra McIntosh et al. (1992) sin modell. Gjennomgående ser det ut til at de refleksjonene som er relatert til fagdidaktiske perspektiver, ofte har et hverdagslig språk og et svakt matematisk fokus.

Selv om lærerne i mange av refleksjonene knyttet til matematiske undervisningsutfordringer trekker inn både matematisk og fagdidaktisk kunnskap, er det interessant å se at de ofte ikke gjør det. En femdel (21 av 98) av utsagna ser ut til å dra veksler på matematisk kunnskap (tabell 3), mens over halvparten (50) indikerer matematikkdidaktisk fokus (tabell 4). I omtrent en tredel (27 av 98) av de ytringene som kan knyttes til matematiske undervisningsutfordringer, er det ingen indikasjoner på at lærerne trekker inn verken faglig eller fagdidaktisk kunnskap. Et eksempel er når lærerne kommer inn på noe som kan knyttes til den matematiske undervisningsutfordringen å stille fruktbare matematiske spørsmål. I mange tilfeller kommenterer lærerne bare at de stiller «åpne spørsmål», uten å komme inn på hvilken matematisk tenking de ønsker å stimulere hos elevene ved å stille et slikt spørsmål, eller hvilket matematisk mål de ønsker å nå fram til. I en annen del av diskusjonene snakker en av lærerne om å bli flinkere til å spørre elevene «Hva tenkte du?» eller «Hvordan kom du fram til det?» Igjen ser det ut til at formålet er mer knyttet til å få elevene til å snakke, heller enn å nå fram til et bestemt matematisk mål. Et annet eksempel er når de kommer inn på noe som kan knyttes til den matematiske undervisningsutfordringen å velge hensiktsmessige representasjoner. Dette er i utgangspunktet en undervisningsutfordring som stiller spesielle matematiske krav til læreren, men vi ser ofte at lærerne snakker mer generelt om hvordan «de svakeste» blant elevene ikke klarer «å overføre det de sitter og holder på med [konkretene] til det som står i boka». Ofte er det også mer praktiske aspekter ved bruken av konkreter som er i fokus. Et tredje eksempel er når lærerne diskuterer hvordan oppgaver kan endres for å bli mer eller mindre utfordrende. Dette er også en matematisk undervisningsutfordring som i utgangspunktet kan stille krav til både spesialisert matematisk kunnskap og fagdidaktisk kunnskap, men også her ser vi flere eksempler på at lærerne snakker mer generelt om at tekstoppgaver kan gi elevene «noe å bryne seg på». Her er det interessant å legge merke til at lærere diskuterte justeringer uten å komme inn på matematikken i oppgavene.

Mange utsagn som ikke har et tydelig matematisk eller matematikkdidaktisk fokus, er knyttet til lærernes refleksjoner omkring valg av oppgaven «Dagens tall er 24». For eksempel forklarer Berit at det er en «åpen oppgave, så den er tilpasset alle ulike nivåer, alle kan få til et eller annet på en sånn oppgave da». Her ser vi indikasjoner på at lærerne ønsker å tilpasse undervisningen til alle elever, og de ser at en åpen oppgave kan være et alternativ. Uttalelsen er generell og inneholder ikke noe spesifikt matematisk fokus eller tydelig bruk av presise vitenskapelige begreper.

Når lærerne blir spurt om hvilke utfordringer de opplevde med en oppgave som «Dagens tall er 24», sier Anne: «… fordi at jeg opplever jo av og til at jeg kan liksom lure på hvordan elevene har tenkt. At jeg ikke alltid skjønner hvordan de har gjort det». Denne uttalelsen kan tolkes som en indikasjon på mangler i den profesjonelle kunnskapsbasen (her SCK).

Avsluttende diskusjon

Hvilke matematiske undervisningsutfordringer som trer fram når lærere diskuterer sin egen undervisning, og hvilke deler av den profesjonelle kunnskapsbasen de selv trekker inn når de diskuterer ulike undervisningsutfordringer knyttet til egen undervisningspraksis, diskuteres i denne artikkelen. Analysene av en gruppe andretrinnslæreres refleksjoner omkring eget undervisningsarbeid med utgangspunkt i oppgaven «Dagens tall er 24» (figur 1) indikerer at mye av det lærerne diskuterer potensielt kan knyttes til lærerarbeidets matematiske undervisningsutfordringer (tabell 1), slik disse er definert av Ball et al. (2008). Lærerne knytter deler av den profesjonelle kunnskapsbasen til de ulike undervisningsutfordringene der å være klar over hva som involveres når en bestemt representasjon tas i bruk og å vurdere om elevers påstander er rimelige er de to mest framtredende.

I den avsluttende diskusjonen ønsker vi å løfte fram to tendenser. For det første er det interessant å merke seg at lærernes refleksjoner ofte mangler et tydelig matematisk eller matematikkdidaktisk fokus – selv når det er snakk om undervisningsutfordringer som stiller krav til spesialisert fagkunnskap. Om lag en femdel (21 av 98) av lærernes utsagn kan knyttes til matematiske undervisningsutfordringer hvor lærerne fokuserer på matematikken (tabell 3). Omkring halvparten (50 av 98) av utsagna som kan knyttes til matematiske undervisningsutfordringer ser ut til å ha fokus på fagdidaktiske perspektiver (tabell 4). Utsagn kodet som fagdidaktiske ser også ut til å ha et relativt svakt matematisk fokus, og de matematiske perspektivene ser ut til å komme i skyggen av det allment didaktiske. En forklaring kan være at de fleste lærere på småskoletrinnet ikke er faglærere; de har elevene i de fleste fag og er utdannet allmennlærere eller grunnskolelærere. Foruten å forholde seg til mange fag, skal de etablere arbeidsvaner og gode relasjoner i tillegg til det faglige innholdet, og det kan muligens forklare det manglende faglige fokuset.

For det andre har vi observert at selv om det kan registreres et fokus på flere deler av den profesjonelle kunnskapsbasen, bruker lærerne ofte et uformelt og hverdagslig språk. Fagbegreper er lite tydelige i lærernes diskusjoner, og der fagbegreper benyttes blir de i liten grad utdypet og presisert. Dette kan tolkes i retning av at det eksisterer en felles profesjonell forståelse knyttet til matematikklærerarbeidets undervisningsutfordringer, og at presisjon og utdyping er unødvendig. Tolkningen kan også gå i retning av at lærerne ikke er i stand til å uttrykke denne tause kunnskapen med presise begreper, eller at de ikke har presise begreper eller felles forståelse. Her trengs videre forskning for å undersøke hvorvidt dette tilsynelatende svake matematiske fokuset i læreres refleksjoner omkring eget undervisningsarbeid henger sammen med manglende profesjonelt kunnskapsgrunnlag eller manglende profesjonsspråk – og hvordan dette eventuelt påvirker elevenes læring. Det kan være en svakhet ved studien at lærerne ikke ble utfordret på å presisere begreper. Vi valgte imidlertid å ikke avbryte lærerne i deres refleksjoner om egen undervisning. Det kan også diskuteres om vi kan si om læreres undervisning er god eller dårlig ut fra språket de bruker i sine refleksjoner om undervisningsarbeidet. Det kan være av betydning å diskutere hvor relevant det er at lærere bruker presise matematikkdidaktiske og matematiske begreper og om de gis tid og mulighet til slike refleksjoner og diskusjoner i hverdagen.

Vi har i artikkelen beskrevet en gruppe andretrinnslæreres refleksjoner, og disse er ikke nødvendigvis overførbare verken til andre andretrinnslærere eller til lærere på andre trinn. En implikasjon av det som er avdekket i studien, kan likevel være at grunnskolelærerlærerutdanningen bør arbeide mer med å utvikle studentenes profesjonelle språk både når de beskriver elevers tenkemåter, men også når de reflekterer rundt eget arbeid. Flere studier påpeker betydningen av et profesjonelt språk (Hoover et al., 2014). De forrige nasjonale retningslinjene for grunnskolelærerutdanningen i Norge løftet fram undervisningskunnskap i matematikk som felles kunnskapsbase (Kunnskapsdepartementet, 2010), men kanskje har ikke utviklingen av denne kunnskapen blitt operasjonalisert godt nok i utdanningsprogrammene. I de nye retningslinjene for femårige grunnskolelærerutdanninger ser det ut til å være et større fokus på praksis (NRLU, 2016), og her kan det være muligheter til å løfte fram og utvikle et mer presist profesjonelt språk knyttet til matematikkundervisning. Implementeringen av de nye femårige grunnskolelærerutdanningene kan gi nye muligheter til å studere hvordan lærerutdanning kan bidra til å utvikle et profesjonelt fagspråk og en profesjonell kunnskapsbase. Vi mener at det kan være hensiktsmessig å fokusere eksplisitt på sentrale matematiske undervisningsutfordringer (jf. Fauskanger & Mosvold, 2016; Hoover et al., 2014) i refleksjoner omkring praksis i lærerutdanningen.

Dette tror vi kan bidra til å synliggjøre hvordan undervisningskunnskapen som skal utvikles gjennom utdanningen er knyttet til praksis, og vi tror også at det kan stimulere til videre utvikling av et profesjonsspråk. Basert på internasjonal forskning hvor sentrale undervisningspraksiser øves på i lærerutdanningen (f.eks. Kazemi et al., 2016; Lampert et al., 2013), samt erfaringer fra etterutdanningsprosjektet Mestre Ambisiøs Matematikkundervisning ved Matematikksenteret, NTNU (f.eks. Fauskanger & Bjuland, 2019; Wæge & Fauskanger, 2020) mener vi at en slik dreining mot undervisningspraksiser kan bidra til ytterligere profesjonalisering av matematikklæreryrket også i Norge.